【Python】ミニマックス法を用いて○×ゲームの必勝を判定する

はじめに

Googleで検索してみたところ5秒で答えが出た。確定で先後引き分けにできるそう。

この時点で表題の意義は失われたも同然だが、この記事の趣旨は実際にプログラミングを用いて局面の全探索を行い、ミニマックス法によって必勝法が存在するかを探索するという過程にある。

また、○×ゲームの進化版としてゴブレットゴブラーズというボードゲームが存在する。本当はこのゲームの必勝法について探索をしたかったのだが1から考察するには少し複雑なので、まずは元祖でありルールが単純な○×ゲームから考察していき、ゴブレットゴブラーズの必勝法を考える際にここでの試行錯誤を生かそうという魂胆である。

p.s. 初投稿です。内容の不備、間違いなどあれば指摘していただけると嬉しいです。

ミニマックス法とは

こちらを参考にさせて頂きました→5分で覚えるミニマックス法

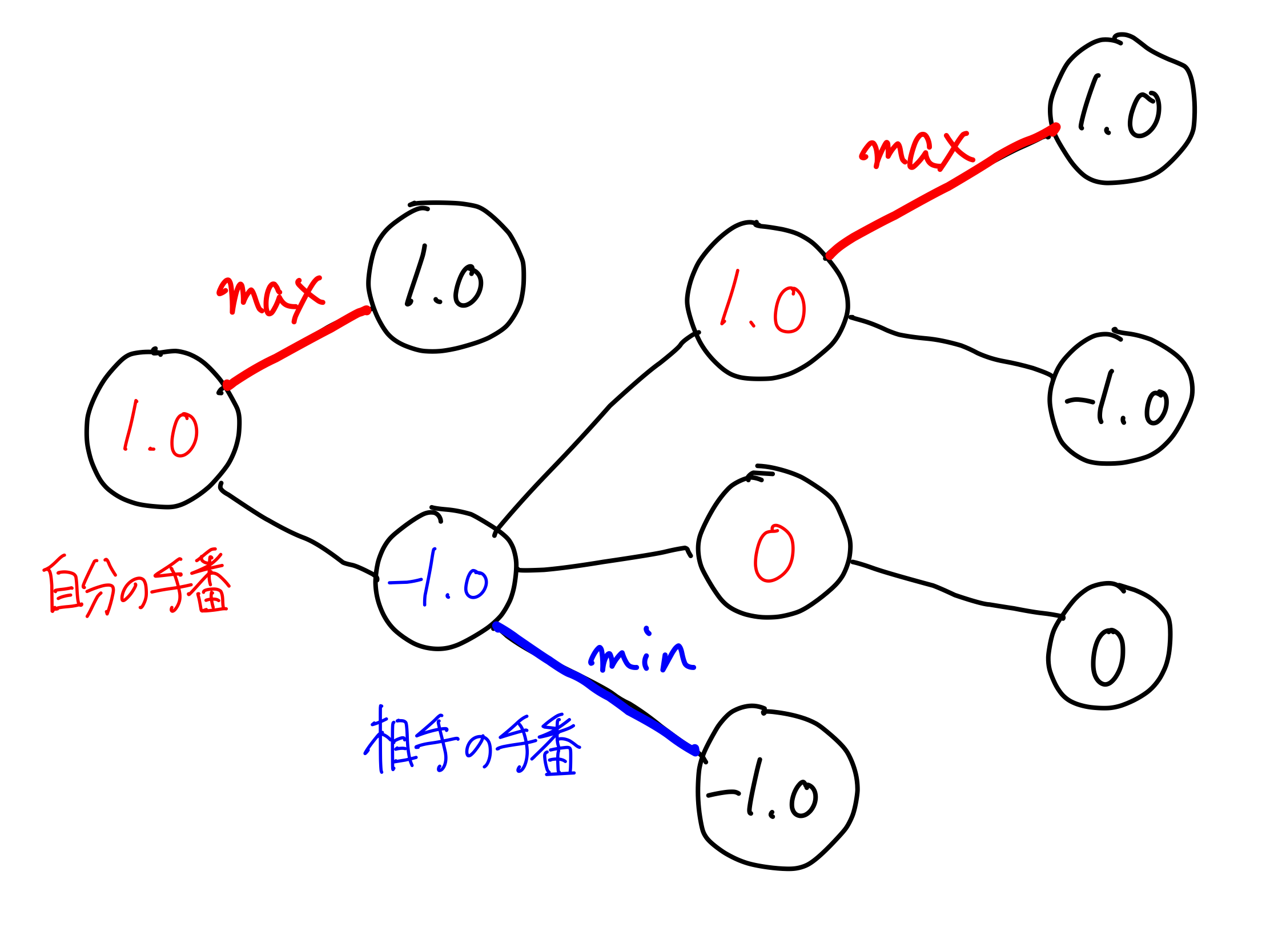
簡潔に言うと、自分の手番の時に被害が最小となる手を、相手の手番の時に自分にとって被害が最大となる手を選んでいくことで局面ごとの最善手を割り出していくという手法。

今回は主にこの手法をメインに実装していく。

実装の手順

目次

項番	タイトル
1	局面ごとに番号をつける
2	DFSにより次にありえる局面を列挙していく
3	ミニマックス法による評価
4	実装
5	折角なのでいろいろ遊んでみる
-	結論
-	ソースコード

1. 局面ごとに番号をつける

ミニマックス法によって割り出した各局面ごとの評価値を配列に格納するために、一つ一つの局面で重複しない番号の付け方を考えていく。

まずは局面としてありえる場合の数を考えていく。
各マス目は「○」「×」「空白」の3通りの値が考えられ、このようなマスが3x3で9つ存在するので、単純に考えれば3の9乗=19683通りということになる。
これを更に改善しようと思えば、回転させておなじになる局面や対称となる局面を減らすことで効率化することが可能だが、19683通り程度であればそのままでも十分高速に求めることができるため今回は無視して考える。

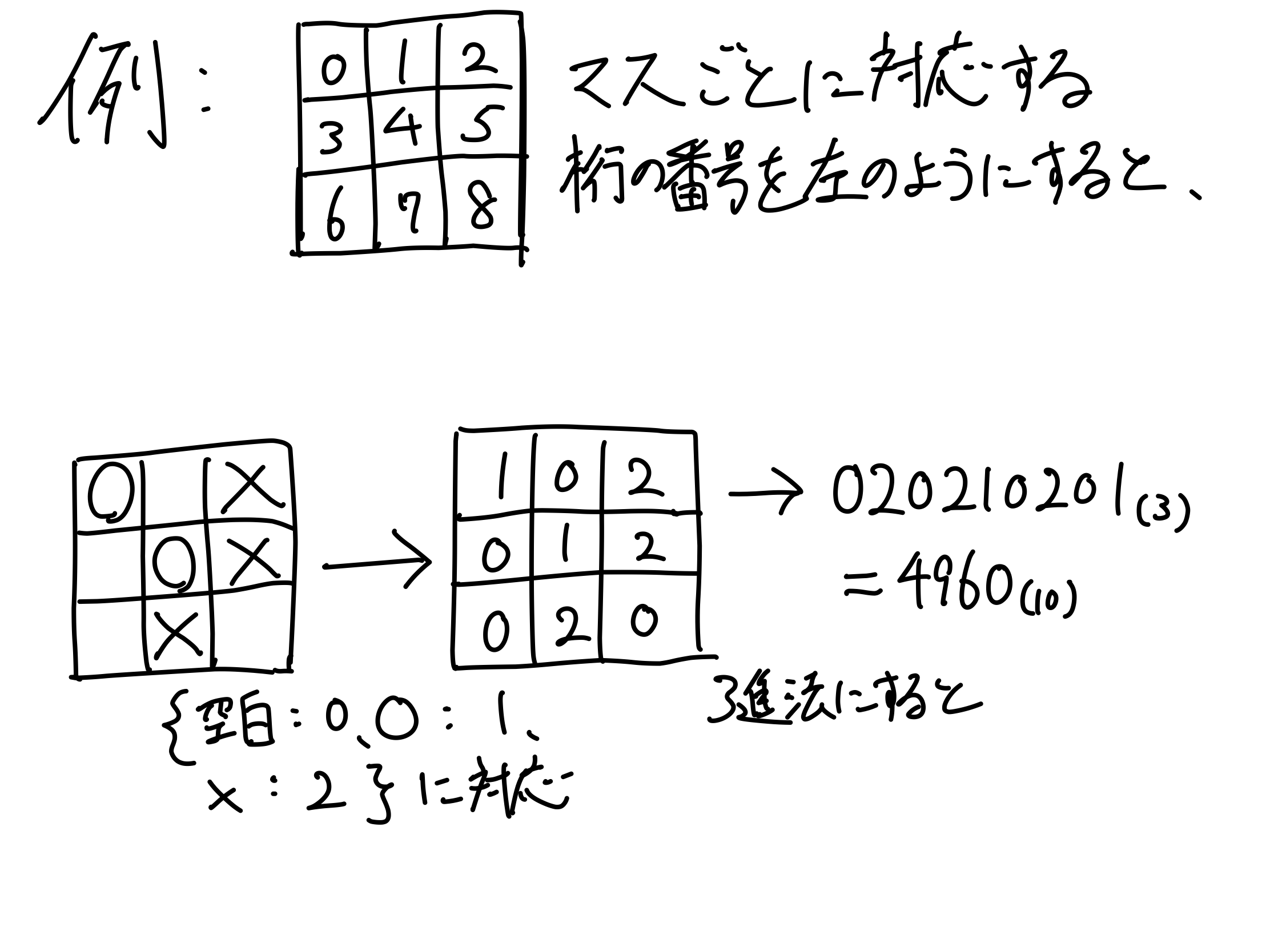
番号は3進法を用いて表すこととする。
下図のように各マスに0~8までの番号をつけ、「空白」なら0、「○」なら1、「×」なら2を状態とし、マスの番号に対応した桁に状態の数を格納することとする。これを10進法に直したときの値を「局面の番号」とする。下図参照

更に今回は、次に来る手番が相手か自分かという情報も入れるため、次に相手が手番の時は求めた局面の番号に3の9乗を加えている。
よって局面の場合の数に自分の手番か相手の手番かという情報が加わり、総合的に場合の数は19683*2=39366通りとなる。

2. DFSにより次にありえる局面を列挙していく

こちらを参考にさせて頂きました→DFS (深さ優先探索) 超入門！ 〜 グラフ・アルゴリズムの世界への入口 〜【前編】

DFSとは深さ優先探索のこと。
今回はBFS(幅優先探索)と比べてメモリの使用量が少なく、またBFSのメリットがあまり生きないと考えたのでこちらを採用した。

また本当は再帰関数で実装したほうがプログラムの長さ的に効率がいいのだと思うが、探索の回数が上限値を超えるとRecursion Errorをはいて面倒だし(上限回数を変更する方法もある)、そのせいで競プロの問題を一つ落としたことがあり個人的に嫌いなので、今回はこの手法を使わなかった。

3. ミニマックス法による評価

冒頭で説明したミニマックス法により局面を評価していく。

まず2のDFSによってゲームが終了となる局面を探す。
この場合○や×が一列に揃っているか、9マス全てに空白が存在しない状態が終了局面となる。自分が勝利する局面を「+1」、自分が敗北=相手が勝利する局面を「-1」、置けるマスがなくなり引き分けとなる局面を「0」と評価値を定める。
終了局面の評価値が定まったら、今度は一つ手前の局面を考える。次にありえる局面の評価値が全て定まっていた場合、

1. その局面が自分の手番だったなら、次の局面の中で最も高い評価値をその局面の評価値とする。
2. その局面が相手の手番だったなら、次の局面の中で最も低い評価値をその局面の評価値とする。

このようなルールで各局面で評価値を定めていくことで、任意の局面や手番において、必勝かどうかが判定できる。
最終的に初手局面(何も置かれていない局面)での評価値が求まれば、このゲームに必勝法が存在するかどうかがわかる。

4. 実装

1~3までを意識しながら実装していった結果がこちら。

from collections import deque
import math

scene_size = 3**9

#局面の番号を状態(n進法のリスト)に変換する
def convert_10ton(x, n):
    li = []
    for _ in range(9):
        li.append(x%n)
        x //= n
    return li

#局面の状態(n進法のリスト)から番号に変換する
def convert_nto10(x, n):
    return sum([x[i]*n**i for i in range(len(x))])

#既に勝敗が決まっている場合評価値を出力する
#戻り値 = (決着がついているか(bool), その場合の評価値(int))
check_li = [(0, 1, 2), (3, 4, 5), (6, 7, 8), (0, 3, 6), (1, 4, 7), (2, 5, 8), (0, 4, 8), (2, 4, 6)]
def check_bingo(x):
    li = convert_10ton(x, 3)
    ret = None
    for items in check_li:
        if li[items[0]] == li[items[1]] == li[items[2]] and li[items[0]] != 0:
            if ret != None: return (True, 0)
            if li[items[0]] == 1: 
                ret = (True, 1)
            else:
                ret = (True, -1)
    if ret: return ret
    if 0 not in li: return (True, 0)
    return (False, None)

#局面の番号から、次にありえる局面を出力する
def list_next_scenes(t):
    li = convert_10ton(t%scene_size, 3)
    new_scenes = deque()
    for i in range(9):
        if li[i] == 0:
            new_scene = t%scene_size+3**i*(turn+1)+(turn+1)%2*scene_size
            new_scenes.append(new_scene)
    return new_scenes

#scenesリストに評価値を格納し、is_confirmedリストに評価値が確定済みか記録する
scenes = [0]*(scene_size*2)
is_confirmed = [False]*(scene_size*2)
todo = deque([0])
while todo:
    t = todo.pop()
    if is_confirmed[t]: continue

    #局面の勝敗が既についている時
    c = check_bingo(t)
    if c[0]:
        scenes[t] = c[1]
        is_confirmed[t] = True
        continue

    #局面の勝敗がついていない時
    turn = t//scene_size
    li = convert_10ton(t%scene_size, 3)
    scene_val = 0
    if turn == 0:
        scene_val = -float('inf')
    else:
        scene_val = float('inf')

    #次の局面としてありえる局面の番号をnew_scenesに格納する
    #既に評価済みの場合、ミニマックス法に基づいて現局面の評価値を計算する
    new_scenes = list_next_scenes(t)
    for scene in new_scenes:
        if is_confirmed[scene]:
            if turn == 0:
                scene_val = max(scene_val, scenes[scene])
            else:
                scene_val = min(scene_val, scenes[scene])
        else:
            break
    else:
        #現局面を評価可能の場合、評価する
        scenes[t] = scene_val
        is_confirmed[t] = True

    #未探索の局面がある場合、探索を続行する
    if is_confirmed[t] == False:
        new_scenes.appendleft(t)
        todo.extend(new_scenes)

#初手局面での評価値を出力
print(scenes[0])

実行結果は「0」であった。これは初手局面での評価値を意味するので、先手後手のプレイヤーがそれぞれ最善の手を指すよう動けば、必ず最終局面の評価値は0になる=引き分けになることが再確認できた。

5. 折角なのでいろいろ遊んでみる

大まかに以下のような改良を行った。

• 任意の局面の情報を入力した場合、必勝判定と最終局面までの手順を出力するようにした。
• 初手局面から推移し得る局面だけでなく、全ての局面で正しく評価値を計算できるようにした。

また入力形式は

n
a0 a1 a2
a3 a4 a5
a6 a7 a8

のようにし、
n = "p"のとき次に○の手番、n = "e"のとき次に×の手番とする
a(n) = {0: 空白, 1: "o", 2: "x"}と定めることにする。

疑問1 二手目はどこに置くべきか

先手を勝たせないために2手目はどこに置くべきか考えてみる。初手に真ん中に置く場合、二手目の置き方は「辺に置く」か「角に置く」の2通りである。それぞれについて検証してみる。

①辺に置く場合

入力

p
0 0 0
0 1 2
0 0 0

実行結果

Player wins in 5 moves
□ □ □
□ o x
□ □ □

Player turn:
o □ □
□ o x
□ □ □

Enemy turn:
o □ □
□ o x
□ □ x

Player turn:
o □ o
□ o x
□ □ x

Enemy turn:
o x o
□ o x
□ □ x

Player turn:
o x o
□ o x
o □ x

end

②端に置く場合

入力

p
0 0 2
0 1 0
0 0 0

実行結果

Draw
□ □ x
□ o □
□ □ □

Player turn:
o □ x
□ o □
□ □ □

Enemy turn:
o □ x
□ o □
□ □ x

Player turn:
o □ x
□ o o
□ □ x

Enemy turn:
o □ x
x o o
□ □ x

Player turn:
o o x
x o o
□ □ x

Enemy turn:
o o x
x o o
□ x x

Player turn:
o o x
x o o
o x x

end

①②より、後手は二手目に角に置かなければ負けてしまうようだ。
皆さんも○×ゲームでやむを得ず後手を選択する場合はくれぐれも気をつけて頂きたい。

疑問2 初手で二手指しすると勝てるか

今度は後手をいじめてみる。順当にやれば引き分けるゲームも、二手指しすればさすがに勝てるのだろうか。最初から真ん中に○が置いてあるという条件でゲームを開始してみる。

入力

p
0 0 0
0 1 0
0 0 0

実行結果

Player wins in 5 moves
□ □ □
□ o □
□ □ □

Player turn:
o □ □
□ o □
□ □ □

Enemy turn:
o □ □
□ o □
□ □ x

Player turn:
o o □
□ o □
□ □ x

Enemy turn:
o o x
□ o □
□ □ x

Player turn:
o o x
□ o □
□ o x

end

流石に勝てた。

結論

ボードゲームを探求するのは面白い。ミニマックス法の基礎は理解できたので、これからは局面数が少なめのボードゲームであれば、全探索とミニマックス法を組み合わせてゴリ押しすることで必勝の判定ができそうだ。
次は冒頭で言及したゴブレットゴブラーズについても必勝法を探ってみたいと思う。

最終的なソースコード

github → https://github.com/ysgrPrograming/ox_judge/blob/main/ox_judge.py