はじめに
前回に引き続きニューラルネットワークの基礎について整理します。
今回は最終的にXOR回路をニューラルネットワークに学習させることがゴールです。
勾配降下法について
ニューラルネットワークの基礎を整理しよう(1)で軽く触れましたが、ニューラルネットワークの目標は出力と正解の誤差ができるだけ小さくなるような重みとバイアスを探すことでした。その目標へのアプローチの一つに勾配降下法があります。あるパラメータ$\omega$について、勾配降下法を用いて更新する様子を以下の式に示します。
$$\omega=\omega-\eta\frac{\partial f}{\partial \omega} -(1)$$
まず、$\eta$は学習率といい、どれくらいの大きさで更新するかの倍率を示しています。この定数は大きすぎると目標とする地点を過ぎてしまい、小さすぎると目標の地点に到達するのにたくさんの計算を要します。適度な値を我々が与えてあげなければいけません。$f$は損失関数を表します。つまり、式(1)は、あるパラメータから損失関数のあるパラメータに関する微分を引き算し続けて、最終的に損失関数の最小値を探し当てる、というプロセスを表しているのです。
勾配計算の実装です。
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
x_shape = x.shape
x = x.reshape([1, x.size])
grad = grad.reshape([1, x.size])
for idx in range(x.size):
tmp_val = x[0][idx]
x[0][idx] = tmp_val + h
fxh1 = f(x)
x[0][idx] = tmp_val - h
fxh2 = f(x)
grad[0][idx] = (fxh1 - fxh2) / (2*h)
x[0][idx] = tmp_val
grad = np.reshape(grad, x_shape)
return (grad)
今回は行列式xを一度、一行の行列に直してから計算しています。その後全ての変数x[i]に対する関数fの微分を計算し、最後はgradをxと同じ形に戻してその行列を返しています。
ソフトマックス関数
では本題のXOR回路の学習に入る前にソフトマックス関数について紹介します。ソフトマックス関数は分類問題における出力層の活性化関数です。活性化関数については前回の記事を参考にしてください。式を以下に示します。
$$y_k=\frac{e^{a_k}}{\sum_{i=1}^{n}e^{a_i} }-(2)$$
これは、出力層の数がn個ある場合の、k番目の出力を表しています。$y_k$は出力値全体$\sum_{i=1}^{n}e^{a_i}$に対するk番目の出力の割合を出力に持ちます。つまり分類問題で考えると、ある入力に対する出力について、どれくらいの確率で各ラベルの状態になっているかということを表しています。ただ指数関数をコンピュータで実装する際は桁が大きくなり過ぎて情報落ちしてしまう可能性があるため式(1)を次のように変形してから実装します。
$$y_k=\frac{e^{a_k+C}}{\sum_{i=1}^{n}e^{a_i+C} }-(3)$$
詳細な計算は省きますが、式(2)の分母と分子に定数Cをかけてみてください。この形になるはずです。式(3)では新たに定数Cが登場しました。この定数Cで出力を正規化しています。(2)と(3)で計算結果は変わりません。では、実装してみましょう。
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
XOR回路を学習させる
XOR回路ってAND回路とかとは違ってパーセプトロンじゃ表せないんです。入出力表を以下に示します。
| 入力$x_{1}$ | 入力$x_{2}$ | 出力$y$ |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
これをニューラルネットワークに学習させるのが今回の本題です。
では実装いきましょう。
import numpy as np
import sigmoid
import cross_empty_error
import numericalgradient
import softmax
import random
import csv
class TwoLayerNet:
def __init__(self, input_size=2, hidden_size=2, output_size=2, weight_init_std=0.1):
self.params={}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_empty_error(y, t)
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_grdient(loss_W, self.params['W1'])
grads['b1'] = numerical_grdient(loss_W, self.params['b1'])
grads['W2'] = numerical_grdient(loss_W, self.params['W2'])
grads['b2'] = numerical_grdient(loss_W, self.params['b2'])
return grads
def learn(self, X, T, step, learning_rate):
for i in range(step):
case = random.randrange(1, 5)
case = str(case)
x = 'x' + case
t = 't' + case
init_x = X[x]
teacher = T[t]
grads = self.numerical_gradient(init_x, teacher)
for key in ('W1', 'b1', 'W2', 'b2'):
self.params[key] -= learning_rate * grads[key]
loss = net.loss(init_x, teacher)
with open('loss_data.csv', 'a', newline='') as f:
writer = csv.writer(f)
writer.writerow([i, loss])
return self.params
T = {}
T['t1'] = np.array([1., 0.])
T['t2'] = np.array([0., 1.])
T['t3'] = np.array([0., 1.])
T['t4'] = np.array([1., 0.])
X = {}
X['x1'] = np.array([1., 1.])
X['x2'] = np.array([1., 0.])
X['x3'] = np.array([0., 1.])
X['x4'] = np.array([0., 0.])
learning_rate = 0.1
step = 30000
net = TwoLayerNet(input_size=2, hidden_size=2, output_size=2)
params = net.learn(X, T, step, learning_rate)
for i in range(1, 5):
case = str(i)
x = 'x' + case
x = X[x]
y = net.predict(x)
print(y)
print(params)
[0.99697848 0.00302152]
[0.00186758 0.99813242]
[0.00188986 0.99811014]
[0.9981763 0.0018237]
{'W1': array([[-6.61308387, -4.98237816],
[-6.60971866, -4.99250007]]), 'b1': array([2.72834728, 7.42964638]), 'W2': array([[ 7.37978264, -7.57974664],
[-7.2676722 , 7.33929759]]), 'b2': array([ 3.43058795, -3.43058795])}
ここでは二層のニューラルネットワークについて学習させました。今まで言葉で説明したものをプログラムに書き起こした感じです。入力とそれに対する正解を与えてあげて、交差エントロピー誤差を計算し、各パラメータに感する偏微分を計算します。その値を元に重みとバイアスを更新していきます。この学習の流れはlearn関数に記述してあります。
今回は出力をone-hot表現を用いて計算しています。なかなかいい精度で学習出来ているのではないでしょうか?
あわせて誤差関数のグラフを示します。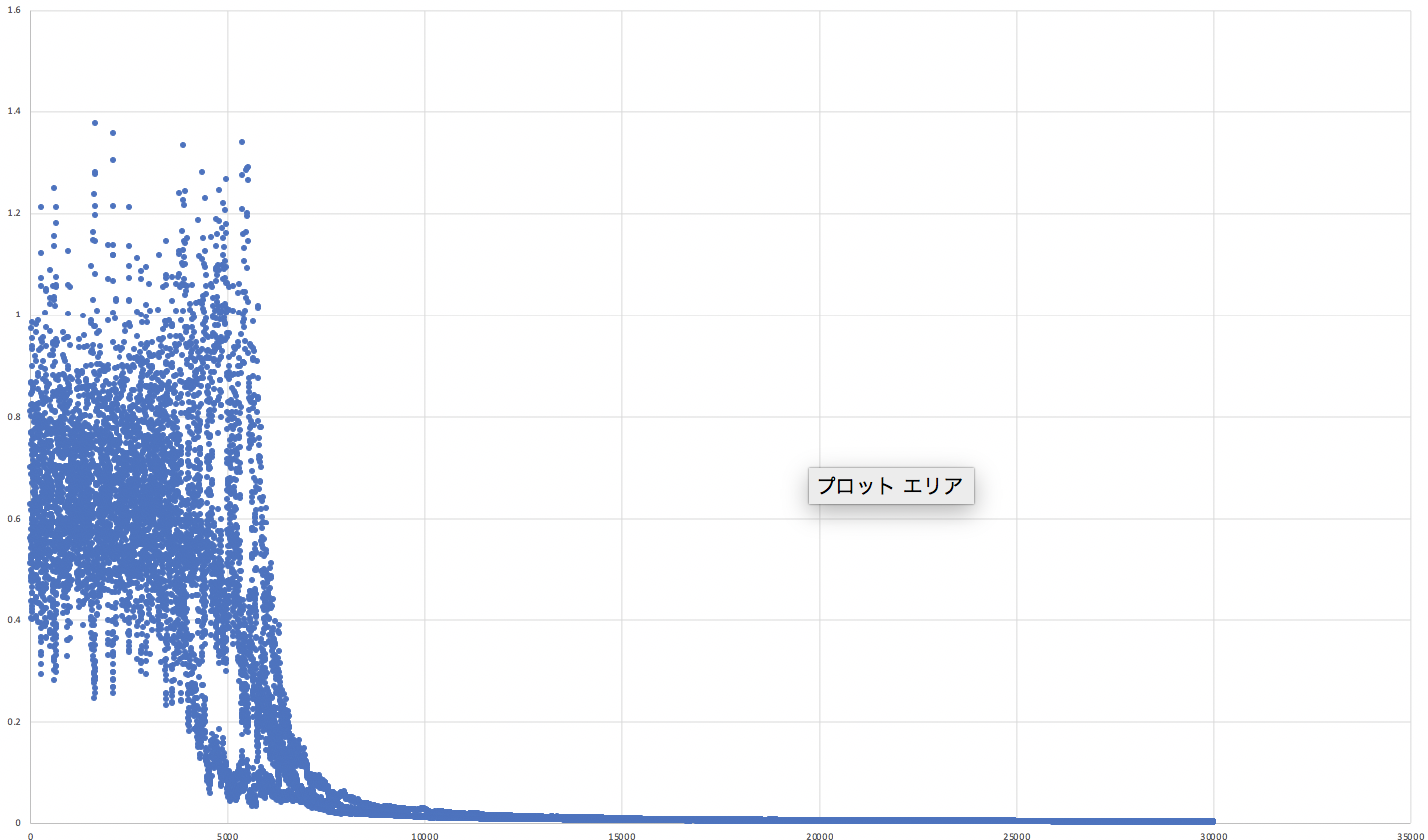
5000ステップくらいまですごく振動しています。おそらく学習率の値が大きかったのかと思われます。何故こうなったかもう少し考察する必要がありそうです...しかし学習が進むにつれて損失関数の値はほぼ0で落ち着いています。学習成功と言ってよいでしょう。
おわりに
今回のニューラルネットワークの学習では割と精度よく実装することができました。しかし、中間層の数が増えると行列計算が膨大になり、またその損失関数の形が複雑になると勾配降下法が通用しなくなったりと結構穴が多いです。ここら辺の穴を補う考え方についてもいつか紹介します。