はじめに
今回初めてQiitaに投稿しようと思い立ち、最近勉強したニューラルネットワークの理論について、備忘録も兼ねて投稿させていただきます。
追記(2021/4/11):補足記事をアップしました。
追記(2021/4/13):Pythonにおけるニューラルネットワークの実装をアップしました。
どうやって勉強したか
「ゼロから作るDeepLearning--Pythonで学ぶディープラーニングの理論と実装」という書籍を読み込みました。今回は前半部分の内容を整理します。
パーセプトロンについて
パーセプトロンとは入出力を兼ね備えたアルゴリズムです。二つの入力値から一つの値を出力するAND回路やOR回路もこのパーセプトロンの一種。今回はAND回路を取り上げて、パーセプトロンとはなんぞや、ということをみていきます。
AND回路の入出力表を示します。
| 入力$x_{1}$ | 入力$x_{2}$ | 出力$y$ |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
要は二つの入力がどちらも1である時、1を出力し、それ以外の時は0を出力するというものです。
ではこの関係を式で表してみます。
y = \left\{
\begin{array}{ll}
0 & (b+\omega_{1}x_1+\omega_{2}x_2 \leq 0) \\
1 & (b+\omega_{1}x_1+\omega_{2}x_2 \gt 0)
\end{array}-(1)
\right.
ここで出てきた定数$b$をバイアス、$\omega_{1},\omega_{2}$を重みと呼びます。さてAND回路を実現するバイアスと重みの組み合わせはなんでしょう?答えは無限にあります。例えば$(b,\omega_{1},\omega_{2})=(-0.7,0.5,0.5)$とした場合です。計算すればたしかにAND回路と同じ出力になっていることを確かめられるはずです。
では(1)を次のように変換してみます。
$$y=h(b+\omega_{1}x_1+\omega_{2}x_2) -(2)$$
h(x) = \left\{
\begin{array}{ll}
0 & (x \leq 0) \\
1 & (x \gt 0)
\end{array}-(3)
\right.
なんてことはないです。式(1)の操作に関数を一つ挟んだような形になっただけです。この新たに出現した関数$h(x)$を活性化関数と呼びます。
ここまでは難しい話もあまりなくすんなり入ってきました。ここから徐々に小難しくなっていきます。
ニューラルネットワークについて
お察しかとは思いますが、ニューラルネットワークもパーセプトロン同様入出力を持ったアルゴリズムです。パーセプトロンと何が違うかというと、先程ぽっと出てきた活性化関数に、ステップ関数(ある値を境に階段のように値が変わる関数)ではなく、シグモイド関数と呼ばれる滑らかな曲線を用いる点です。シグモイド関数とそのグラフを以下に示します。
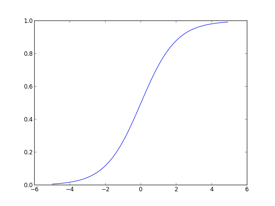
$$h(x)=\frac{1}{1+e^{-x}}-(4)$$
ではなぜニューラルネットワークではステップ関数ではなくシグモイド関数を用いるのでしょうか?後ほど整理します。
ニューラルネットワークの学習
さて本題です。我々が普段AIと呼んでいるものはどのようなものでしょう。コンピュータが人間のように考えること。自動運転。はたまた人類を滅ぼすために未来からやっていきたロボット。色々なイメージがあると思います。それらに共通しているものは、「機械が人の手を借りずに判断を下している」ということです。ニューラルネットワークに関して言えば、入力されたデータから、コンピュータが自分で重みとバイアスを決定します。これがニューラルネットワークの学習です。そのプロセスについて解説します。
損失関数の導入
機械が勝手に学習するとはいってもなにか指標を与えて挙げないとコンピュータは動くに動けません。そこで登場するのが損失関数です。一般的に2乗和平均誤差や交差エントロピー誤差を用います。難しい言葉が出てきました。ものすごく噛み砕いて表現すると機械が学習の過程で出した答えと正解との誤差のことです。精度が良いとはつまりできるだけ正解に近い答えを導出できることでしょう。ニューラルネットワークでは精度を良くするために、損失関数という誤差をできるだけ0に近づける、という指標をもとに学習を行います。
勾配法の導入
さて学習の指標を立てることはできましたが、どのようなアプローチを取れば良いのでしょうか?正解は微分(勾配)です。微分とは、ある点において変数の値を微小に増加させたとき関数の値がどのように変化するか示したものです。ゴールは誤差、つまり損失関数の値ができるだけ小さくなる点を求めることでした。ある重みに関する損失関数の偏微分の値が正であればその重みを減少させ、負であれば増加させる。このようにして全ての重みパラメータを更新していけばいずれ損失関数の最小値に辿り着くはずです。しかしながら例外もあります。それについては次回以降の記事で紹介します。
ここで重要なのは更新する値が微小なものであるということです。もしも活性化関数にステップ関数を用いた場合、重みの微小な変化による出力の変化は活性化関数によってなかったことにされてしまいます。これがニューラルネットワークにおいて活性化関数にステップ関数ではなく滑らかで微分可能な関数を用いる理由です。
まとめ
ここまで駆け足になりましたがニューラルネットワークの学習過程について大まかな流れをまとめられたかと思います。次回以降も今回省いた活性化関数や損失関数、勾配法のPythonによる実装など備忘録として更新していきます。初めての投稿のため、稚拙な部分が多々見受けられると思いますが、筆者の成長も一緒に見守っていただけると幸いです。