はじめに
前回の記事で詳しく扱わなかった部分について、Pythonで実装しながら補足します。
活性化関数
おさらいしておくと、活性化関数とはニューラルネットワークにおいて、入力信号を出力信号に変換する関数でした。簡単な図に示すとこのような感じです。
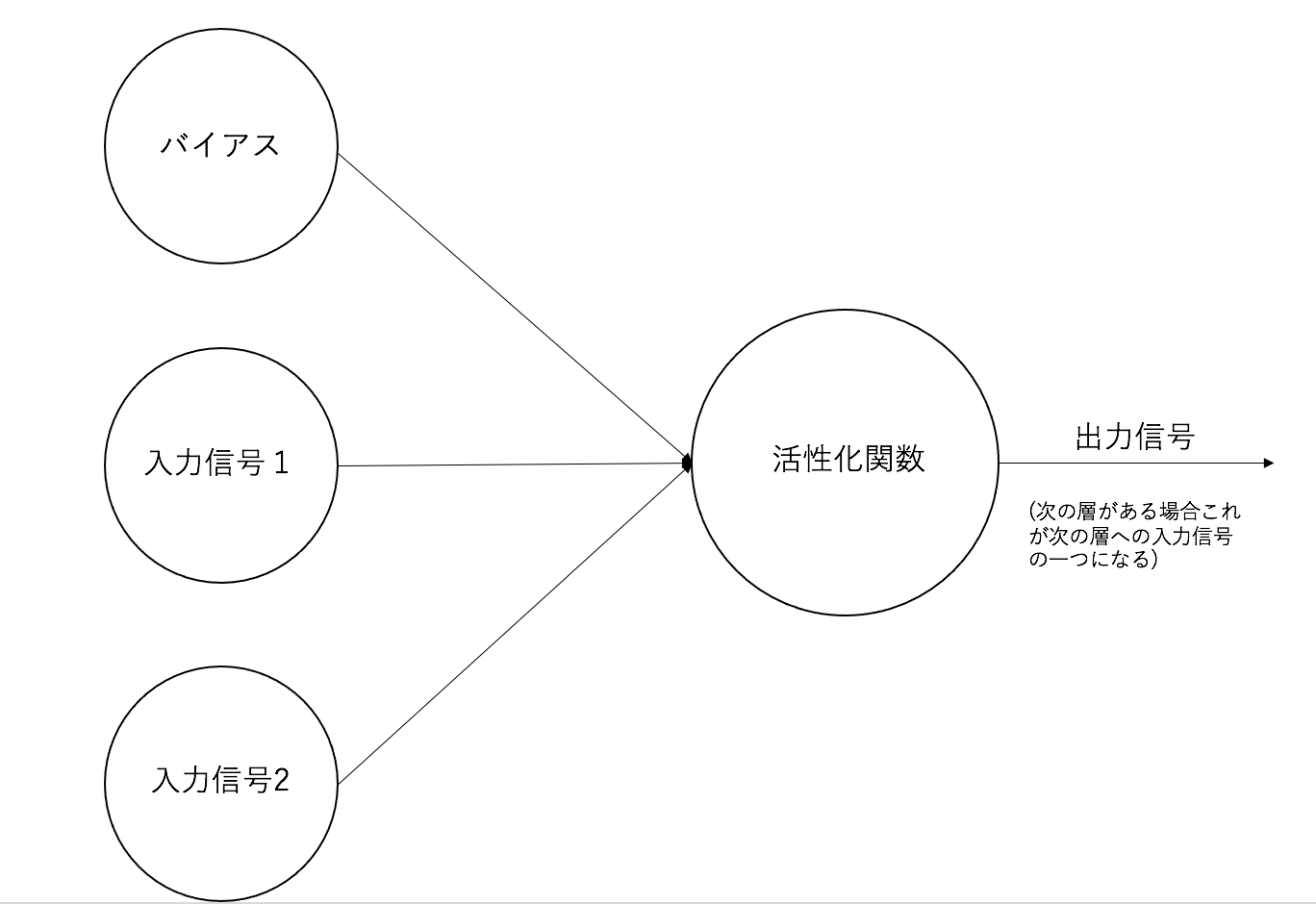
ニューラルネットワークでは活性化関数にシグモイド関数を用います。シグモイド関数は次の式で表せました。
$$h(x)=\frac{1}{1+e^{-x}}-(1)$$
なぜこの関数を用いるかについては前回の記事にて説明しているのでそちらも読んでいただけると幸いです。早速シグモイド関数を実装してみましょう。
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
Pythonではブロードキャスト機能が備わっているため、このように行列に対する計算も簡単に実装することができます。ここでsigmoid()の引数には入力信号の総和を代入しています。
損失関数
前回の記事で損失関数とは、正解の値とニューラルネットワークネットワークが学習によって導き出した出力の誤差であり、その値を小さくすることを指標に重みとバイアスを更新していく、と説明しました。しかしどうもふわふわしています。ではこの損失関数をどのように定量化しているかみていきましょう。
二乗和平均誤差
一般的に、損失関数には二乗和平均誤差と交差エントロピー誤差のどちらかが用いられます。まず二乗和平均誤差について説明します。式で表すと以下の通りです。
$$E=\frac{1}{2}\sum_{k}(y_{k}-t_{k})^{2} -(2)$$
ここで$y_k$はある入力信号に対してニューラルネットワークが導き出した出力、$t_k$はその入力に対して我々人間が正解と定義している値です。例えばAND回路において入力を(1, 1)とするとその出力は1であることが正解です。二乗和平均誤差はこの出力と正解の差を二乗して全て足し合わせることでニューラルネットワークの出力と正解との乖離を定量化しているのです。
ではこれも実装しましょう。
import numpy as np
def squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
たとえば正解の値tが10 であり、ニューラルネットワークの出力yが8の場合と6の場合で二乗和平均誤差の値を比べてみましょう。
t = np.array([10])
y_1 = np.array([8])
y_2 = np.array([6])
error_1 = squared_error(y_1, t)
error_2 = squqred_error(y_2, t)
print(error_1, error_2)
2.0 8.0
前者の値の方が小さいです。これは前者の出力と正解との誤差が後者のそれよりも小さいということを表しています。つまり前者の出力の値は後者の出力の値に比べて正解の値に近いということです。タブの出力は誤差を算出するプログラムの出力を意味しているので混同しないように気をつけてください。
交差エントロピー誤差
続いて交差エントロピー誤差についてみていきます。式で表すと以下の通りです。
$$E=-\sum_{k}t_{k}\log{y_k} -(3)$$
$y_k$と$t_k$については二乗和平均誤差の説明で用いたものと同じです。ただし一つだけ大きく違うことがあります。それはこれらの値の持つ性質です。先ほどの二乗和平均誤差においては正解の値に連続値を用いました。ある数値が欲しい問題については二乗和平均誤差を用いることが多いです。
では交差エントロピー誤差はどのような問題を評価するときに登場するのでしょうか?
分類問題とone-hot表現
正解は分類問題です。例えばある特徴に関する入力を元に、猫か犬か判断する問題があるとします。ではこの問題を天下のコンピュータ様に解いてもらいましょう。しかし悲しいかな、コンピュータは万能ではありません。ただ万能に見えるだけで、実際は0と1を使った計算しかしていないないのです。当然人間の言葉はわかりません。では猫と犬というものをどのように表現してあげればよいでしょうか?
ここで登場するのがone-hot表現という考え方です。この考え方では0と1の組み合わせを用います。0は偽、1は真を表しています。例えば、猫であるかどうかを表す要素を一つ目に、犬であるかどうかを表す要素を二つ目に記述するものとします。それでは(1, 0)と(0, 1)という値の組み合わせはそれぞれ何を表すか考えてみましょう。0は偽、つまり、ある状態ではない、ということを表し、1は真、つまり、ある状態であるということを示しています。それを踏まえると(1, 0)という値の組みは、猫という状態であり、犬という状態ではない、つまり猫を表しているということがわかります。同様にして(0, 1)は犬を表しているということもわかるはずです。この考え方は便利で、ラベルを増やせば簡単に分類する項目を増やせるのです。たぬきでも狐でも好きなの入れてください。
改めて交差エントロピー誤差の実装
閑話休題。
交差エントロピー誤差は分類問題で用いること、分類問題では正解の値は、例えば(0, 1, 0, 0)のようにone-hot表現をもとに、正解のラベルの値のみ1があり、それ以外のラベルの値は0であることを意識してください。もう一度式(3)を召喚します。
$$E=-\sum_{k}t_{k}\log{y_k} -(3)$$
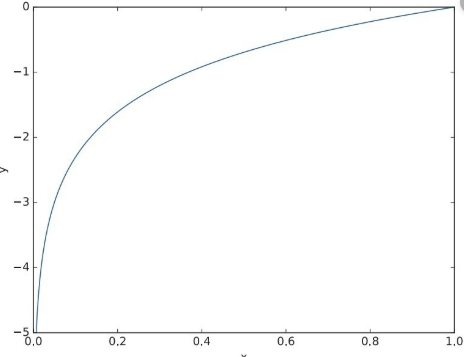
正解のラベルだけ1なんだ...あ、じゃあ$t_k$の値が1のとこと同じラベルのとこの値をlogにつっこんだやつじゃん。なんだそれだけか。それだけです。$y=\log{x}$のグラフを見てみます。$x$が1に近いほど$-y$の値に近づいています。これってつまり正解ラベルの値が1に近ければこの値が少なく、0に近いほどこの値が大きくなっています。この性質は確かに分類問題を扱う上では非常に便利です。
では交差エントロピーを実装します。
import numpy as np
def cross_empty_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
delta は、y の値が0のときにlogの中身が0にならないために導入しました。では適当に値を入れて交差エントロピー誤差がどのように変化するかみていきましょう。
t = np.array([0, 0, 1, 0, 0])
y_1 = np.array([0.1, 0.04, 0.7, 0.1, 0.06])
y_2 = np.array([0.1, 0.7, 0.04, 0.1, 0.06])
print(cross_empty_error(y_1, t), cross_empty_error(y_2, t))
0.3566748010815999 3.2188733248713257
tの3番目の値を正解として用意しました。正解ラベルに対するy_1,y_2 の値はそれぞれ、0.7, 0.04です。
出力をみてみると確かに、正解ラベルに対する出力の値が1に近いほど交差エントロピー誤差の値が小さくなっています。
すごく便利です。気づいた人天才ですね。
おわりに
前回の記事で重要であったにも関わらずふわっと終わってしまった損失関数の定量化をメインに投稿しました。次回はこれらの関数を用いて、実際にニューラルネットワークに学習させる過程をまとめるつもりです。
私ごとですが、徐々にMarkdown記法に慣れてきました。さらに慣れて投稿にかける時間を短縮するためにも、これからどんどん投稿していこうと思います。