ポアソン分布と指数分布の両方を紹介する理由
ここでは,
- ポアソン分布を用いて時系列データを等時間間隔を生成する方法
- 指数分布でイベントリストを生成する方法
の両方を紹介する.どちらもポアソン過程(レアイベントで,定常で,過去に依存しない)を,発生確率で見たのがポアソン分布で,到来時刻で見たのが指数分布となる.ポアソンで生成する方法は,等間隔な時間でサンプルした場合によく使われる.指数分布は,光子が一つ一つ到来した時刻を生成する(ここではイベントリストと呼ぶ)場合に使われる.どちらも兄弟のような関係なので,一緒に覚えておいた方がよいでしょう.
説明不要で,ソースコードだけで十分,という方は,
をご覧ください.
指数分布とポアソン分布の関係性について、数学的な話は、
に書いてますので、こちらを参考にしてください。
関連するページ
- パワースペクトルに位相ランダムを仮定して時系列データを生成する方法
- matplotlibとscipyのフーリエ変換(FFT)を用いてパーシバルの定理を確認する方法
- 対数正規分布 log-normal する 1次元と2次元のデータ生成方法
- Lomb-Scargle ペリオドグラムの時間ビンとエイリアスの関係を astropy で理解する
基礎のおさらい
ポアソン分布
平均値 $\lambda$ のポアソン分布は,
p(n) = \frac{\lambda^n}{n !} e^{-\lambda}
とかける.ポアソン分布はパラメータが一つであり,平均値も分散も一個のパラメータで確定する.ここで,関数の変数 $n$ は 0 以上の正の整数であることに注意しよう.つまり,この式は確率密度分布ではなく,確率であり,この値が1個を超えることはない.
平均値 $\lambda$ は,単位時間あたりの平均的な量なので,これは正の実数で構わない.1秒あたりの平均的な値でもよいし,一時間あたりの量でも構わない.自分の設定した単位時間当たりの平均的な数がわかれば事象の発生確率が予言できる.
ポアソン分布は良質な参考文献がたくさんあるので,詳細は他を参考ください.
指数分布
単位時間当たりの平均的なイベント発生率を $\lambda$ とする指数分布は,
p(t) = \lambda e^{-\lambda t}
となる.あるいは,寿命 $\tau = 1/\lambda $ を用いて,
p(t) = \frac{1}{\tau} e^{- t/\tau}
と書くことが多い.ここで,変数 $t$ はポアソン分布と違って,正の実数であることに注意しよう.つまり,確率密度であり,個々の値は1よりも大きくなっても良い.
時刻 $t$ でイベントが発生する確率であり,どのくらいの時間が経てば,ランダムな事象が一回発生するのかを予想してくれる.
ポアソン分布でライトカーブを生成する方法
まずは,ポアソン分布で時系列データ(ここでは,光子の検出を想定していて,ライトカーブと呼ぶ)を生成する方法を見てみよう.
カウントレートが一定の場合
超基本だが,一定のカウントの場合をまずは考えてみる.
200秒間で,ビン数200,平均カウントレート 16 c/s の場合,numpy.random.poisson を用いて,
import numpy as np
import matplotlib.pyplot as plt
tmax=200. # seconds
tbin=200 # number of time bins
meanrate=16. # Hz
time=np.linspace(0,tmax,tbin) #
dt = tmax/tbin # sampling time
const = np.random.poisson(lam = meanrate, size = tbin)
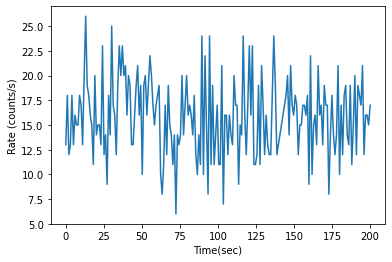
plt.plot(time,const)
plt.xlabel("Time(sec)")
plt.ylabel("Rate (counts/s)")
のように,擬似的な時系列データを生成できる.numpy.random.poisson の size にほしいデータ数( この場合は200)を指定した.
次に,パワースペクトルを生成し,挙動を確認しよう.
import matplotlib.mlab as mlab
def dofft(input,dt):
psd2, freqlist = mlab.psd(input - np.mean(input), # subtract constant
len(input),
1./dt,
window=mlab.window_hanning,
sides='onesided',
scale_by_freq=True
)
psd = np.sqrt(psd2)
return freqlist, psd
freqlist, psd = dofft(const,dt)
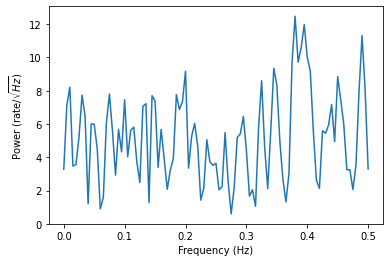
plt.plot(freqlist,psd)
plt.xlabel("Frequency (Hz)")
plt.ylabel(r"Power (rate/$\sqrt{Hz}$)")
このように,統計が悪いので,パワースペクトルもバタバタする.ポアソン過程は過去に依存しないランダムな過程なので,パワースペクトルはフラットになる(=パワーが周波数に依存しない).
周期的な変動 + 一定の定常成分の場合
次に,定常成分に,周期的な変動を加えてみよう.
numpy.random.poisson の size を指定しないと一つだけ生成される.ここでは,引数の lam (=ポアソン分布の平均値)を A sin (2pi ft) + A のように,時事刻々と変更させて生成させた.
import math
tmax=200. # seconds
tbin=200 # number of time bins
meanrate=16. # Hz
time=np.linspace(0,tmax,tbin) #
dt = tmax/tbin # sampling time
const = np.random.poisson(lam = meanrate, size = tbin)
sin=[]
A = 10 # Hz
fr = 0.2 # frequency
for onetime in time:
onesin = A * math.sin(2* math.pi * fr * onetime) + A # f(t) = A sin(2pi ft) + A
onesin_poi = np.random.poisson(lam = onesin)
sin.append(onesin_poi)
sum = sin + const
plt.plot(time,const,label="const")
plt.plot(time,sin,label="sin")
plt.plot(time,sum,label="sin + const")
plt.xlabel("Time(sec)")
plt.ylabel("Rate (counts/s)")
plt.legend()
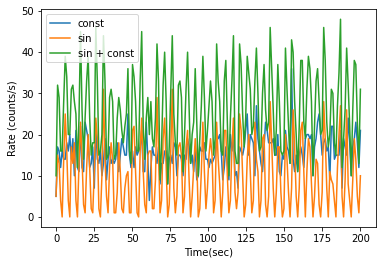
3つの曲線は,それぞれ,
- sin = 10 sin(2pi 0.2 t) + 10
- const = 16 (定常)
- sin + const = sin + const
に対応している.
これもパワースペクトルを作って確認しよう.
freqlist, psd_const = dofft(const,dt)
freqlist, psd_sin = dofft(sin,dt)
freqlist, psd_sum = dofft(sum,dt)
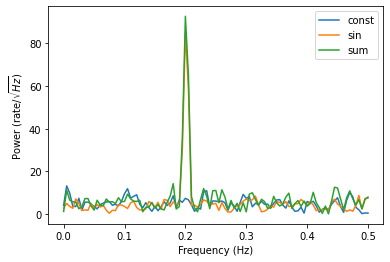
plt.plot(freqlist,psd_const, label="const")
plt.plot(freqlist,psd_sin, label="sin")
plt.plot(freqlist,psd_sum, label="sum")
plt.xlabel("Frequency (Hz)")
plt.ylabel(r"Power (rate/$\sqrt{Hz}$)")
plt.legend()
予想通りに 0.2 Hz にピークが見ている.ノイズがあると,S/Nが悪くなり,検出が難しくなる.
指数分布で光子イベントリストを生成し,ライトカーブを生成する方法
指数部分の乱数発生も numpy.random.exponential を用いて発生させてもよいが,逆関数が簡単に求められるので,逆関数法による乱数発生を紹介する.詳細は,
によくまとまってるので参照されたい.
簡単にまとめると,指数分布の累積分布関数 F(t) の逆関数に,0 ~ 1 の一様乱数 U を用いて,
F_X^{-1} (t) = - \frac{1-U}{\lambda}
を計算するだけでよい.
定常的な場合
設定はポアソンの場合と同じで,平均的なレートが 16 c/s の場合を考える.
import math
import random
tmax=200. # seconds
tbin=200 # number of time bins
meanrate=16. # Hz
nevent = tmax * meanrate # total counts
time=[]
dtlist=[]
ct = 0.
time.append(ct)
for i in range(int(nevent)):
p = random.random()
dt = -math.log(1.0 - p)/meanrate
dtlist.append(dt)
ct = ct + dt
time.append(ct)
(a_hist, a_bins, _) = plt.hist(time, bins=tbin)
xbin_size=a_bins[1] - a_bins[0]
#print(a_hist) print(a_bins)
plt.xlabel("Time (sec)")
plt.ylabel("counts / " + str("%0.3e" % xbin_size) + " (sec)")
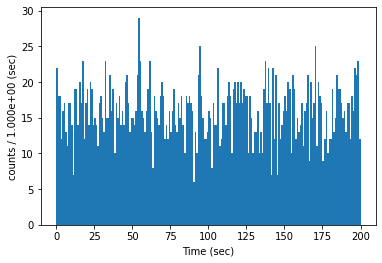
0 から 200 秒の間を,200個のビン数でヒストグラムを生成したので,一ビンのサイズは1秒であり,縦軸は,入力した 16 c/s とほぼ一致する.
周期関数 + 定常成分の場合
では,次に周期関数と定常成分の足し合わせを生成してみよう.
import math
import random
tmax=200. # seconds
tbin=200 # number of time bins
meanrate=16. # Hz
A = 10 # Hz
fr = 0.2 # frequency
nevent = tmax * (meanrate+A) * 2 # total counts + margin
time=[]
dtlist=[]
ct = 0.
time.append(ct)
def getrate(time):
onesin = A * math.sin(2* math.pi * fr * time) + A
return onesin
for i in range(int(nevent)):
p = random.random()
onesin = getrate(ct)
totalrate = meanrate + onesin
dt = -math.log(1.0 - p)/totalrate
dtlist.append(dt)
ct = ct + dt
time.append(ct)
(a_hist, a_bins, _) = plt.hist(time, bins=tbin, range=(0,tmax))
xbin_size=a_bins[1] - a_bins[0]
#print(a_hist) print(a_bins)
plt.xlabel("Time (sec)")
plt.ylabel("counts / " + str("%0.3e" % xbin_size) + " (sec)")
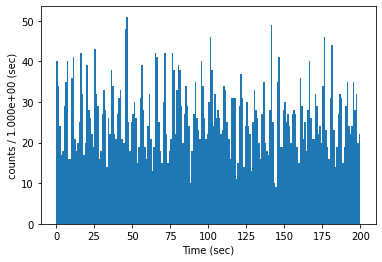
これで,定常成分と振幅が10の周期関数が含まれる.
パワースペクトルを計算して,周期を確認しよう.
freqlist, psd = dofft(a_hist,xbin_size)
plt.plot(freqlist,psd)
plt.xlabel("Frequency (Hz)")
plt.ylabel(r"Power (rate/$\sqrt{Hz}$)")
plt.legend()
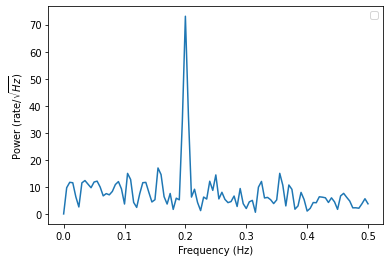
自分で入力した 0.2 Hz の周波数のところにピークが立っている.
光子のイベントリスト
この方法は,一つ一つの光子の到来時刻をシミュレーションできるので,サンプリング間隔が非一様であっても使えるので,時間方向への自由度が高い.