Lomb-Scargle ペリオドグラムの時間ビンとエイリアスの関係を astropy で理解する

前提

Lomb-Scargle ペリオドグラムを使うときには，エイリアスや時間ビンに気をつける必要がある．ここでは， astropy.timeseries を用いて実例で説明する．

フーリエ変換や，擬似的なライトカーブの生成方法は，ポアソン分布と指数分布を用いてpythonで擬似的な時系列データを生成する方法 などで理解していることが前提です．

エイリアスは，多義的な使われ方するので注意が必要です．http://www.ic.is.tohoku.ac.jp/~swk/lecture/yaruodsp/win.html の sinc 関数のように，サイドローブのことをエイリアス，という人もいます．アンチエイリアスフィルターの“エイリアス“は，第２ナイキストゾーン以上の周波数の影響を除くという意味で，指しているものは全然違います．alias というは，“偽物“という意味しかないので，それがさすのは文脈によります．ここでは，第２ナイキストゾーン以降に見える繰り返し信号のことをエイリアスと呼んで，このエイリアスの量がLomb-Scargle ペリオドグラムだと時間幅に依存することを確認します．

Lomb-Scargle ペリオドグラム と離散フーリエ変換の違い

細かい事を抜きにすると、Lomb-Scargle ペリオドグラムは、

f(\omega) = \sum_k^N c(t_k) \exp(-i \omega t_k)   

であり、離散フーリエ変換は、

f(\omega_j) = \sum_k^N c(t_k) \exp(-i \omega_j k)   

\omega_j = \frac{2\pi j}{N}

である。前者は、$\omega$ が任意の実数が取れる。後者は、$\omega_j$ が取れる値が限定されている。この違いは、実際にLomb-Scargle ペリオドグラムを作成するときには、データ c(t_k) と 時間 t_k のペアが必要になるのに対して、離散フーリエ変換は時間的に等間隔なデータが前提であり、データ c(t_k)のみだけで計算されることの違いとして現れる。

いわゆる Lomb-Scargle ペリオドグラムは、カイ２乗検定が使えるように、規格化に工夫がされているものが普通であるが、任意の実数の周波数でフーリエ変換を実直に計算することが本質的に重要な点である。

一般論

周期を求めるには万能な方法はない．　
例えば， https://iopscience.iop.org/article/10.3847/1538-4365/aab766
「... while Graham et al. (2013a) instead take an empirical approach and find that when considering detection efficiency in real data sets, no suitably efficient algorithm universally outperforms the others.」と言っていて，Graham et al. (2013a) は、 https://academic.oup.com/mnras/article/434/4/3423/963890 の論文のことです。要するに，ベストな方法は現実のデータによりけり，ということ． LSも万能ではないが，ここではフーリエ変換とは少し違う使い方のポイントについて解説する．

コードの一覧

google Colab にコードの一式を載せている．

これの最後の方にLSについての紹介がある。
コード読めばわかる人はこちらを参照ください．

等しい時間間隔の場合の Lomb-Scargle ペリオドグラム

等時間間隔の時系列データの生成

ポアソン分布する0.2Hzのsin波をイベントファイルから生成する．

詳細は，ポアソン分布と指数分布を用いてpythonで擬似的な時系列データを生成する方法を参照のこと．

import math 
import random
tmax=200. # seconds
tbin=200 # number of time bins
meanrate=16. # Hz
A = 10 # Hz 
fr = 0.2 # frequency 
nevent = tmax * (meanrate+A) * 2 # total counts + margin

time=[]
dtlist=[]
ct = 0.
time.append(ct)

def getrate(time):
  onesin = A * math.sin(2* math.pi * fr * time) + A  
  return onesin

for i in range(int(nevent)):
  p = random.random() 
  onesin = getrate(ct) 
  totalrate = meanrate + onesin 
  dt = -math.log(1.0 - p)/totalrate
  dtlist.append(dt)
  ct = ct + dt 
  time.append(ct)

(a_hist, a_bins, _) = plt.hist(time, bins=tbin, range=(0,tmax))

Lomb-Scargle の実行

from astropy.timeseries import LombScargle
t = a_bins[:-1]
y = a_hist
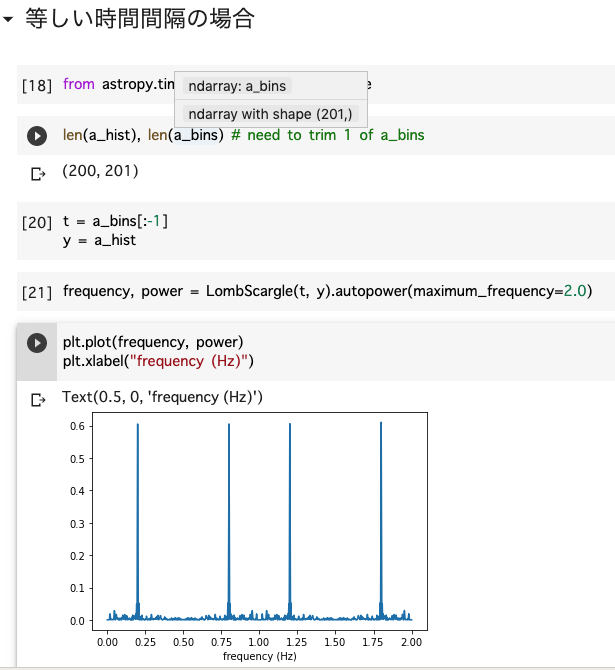
frequency, power = LombScargle(t,y).autopower(maximum_frequency=2.0)
plt.plot(frequency, power) 

実行結果は，

のように， 0.2Hzの真の波に対して，ナイキスト周波数 0.5 Hz を境に，周期構造となる．

非一様な時間間隔の場合の Lomb-Scargle ペリオドグラム

非等時間間隔の時系列データの生成

randt = [] 
tmpt = 0.
randt.append(tmpt)
for oner in np.random.rand(len(t)): # len(t)分だけ，乱数で時間刻みを発生させる．
  tmpt += oner 
  randt.append(tmpt)
(hist_rand, bins_rand, _) = plt.hist(time, bins=randt) # randt の配列(時間間隔がランダム)にしたがって，ライトカーブを生成する．

ライトカーブを生成するときに， bins というオプションにランダムな時間間隔を入れている．この場合のナイキスト周波数の近似値として，時間間隔の平均値を使うこともある．最大周波数は最小の時間間隔で決まる．また，非等間隔だが，最小値が有限で固定値がある場合は，それで実質的に最大の周波数が決まることになる．

dt_rand = np.diff(bins_rand) # 時間間隔を取得
t_rand = 0.5 * bins_rand[1:] + 0.5 * bins_rand[:-1] # ヒストグラムの時間ビンの真ん中を取得 　
y_rand = hist_rand 
mint = np.amin(np.diff(t)) # 最小の時間ビンを取得
fn_rand = 0.5 / mint # 近似的なナイキスト周波数を取得
print("Nyquist frequency = ", fn_rand, " Hz") 
rate_rand = y_rand/dt_rand # カウント数から，　カウント/sec に変更
plt.plot(t_rand, rate_rand)
plt.xlabel("time (sec)")

カウント数ではなく，カウントレートに変更する．

Lomb-Scargle の実行

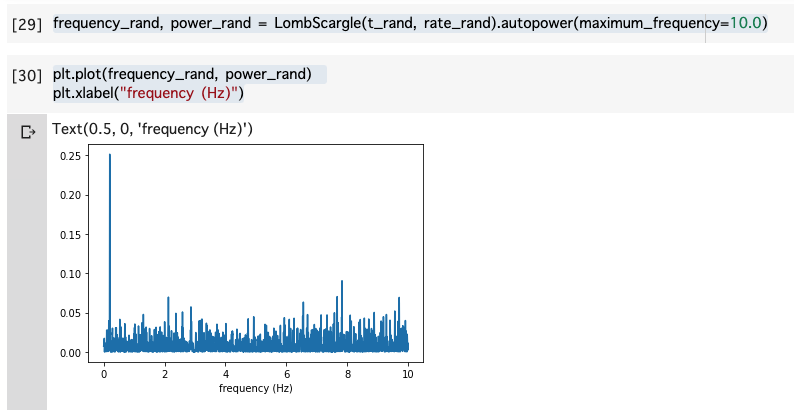
frequency_rand, power_rand = LombScargle(t_rand,rate_rand).autopower(maximum_frequency=10.0)
plt.plot(frequency_rand, power_rand) 
plt.xlabel("frequency (Hz)")

このように，エイリアスが減った．その理由は，時間間隔が非一様なため，ナイキスト周波数がうんと高くなったためである．

そのほか

data gap がある場合もエイリヤスが出やすい。最大周波数を大きくした上で、ビンまとめすることで連続成分は見やすくなる。この辺りは、

の最後の方に例があるので参照ください。

ビンまとめについては、

を参照ください。

まとめ

• 時間的に等間隔の場合は，ナイキスト周波数で周期的になる．
• 時間的に完璧にランダムな非等間隔の場合，ナイキスト周波数が存在しないので，真の値に近い時が一番よい値になる．