Pythonの2つの最小二乗フィッティング手法(scipy.optimize.least_squaresとiminuit)の詳細解説と実例

Last updated at 2025-07-03Posted at 2025-07-03

はじめに

最小二乗フィッティングは、物理学のデータ解析で頻繁に用いられる手法です。特に、観測データとモデル関数のずれ（残差）の二乗和を最小化することで、モデルのパラメータを推定します。Pythonには様々なフィッティング手法がありますが、本記事では2つの代表的な最小二乗フィット手法を比較・解説します:

SciPyの scipy.optimize.least_squares を用いた非線形最小二乗フィット（ヤコビアン行列を利用し、numpy.linalg.inv または numpy.linalg.pinv で誤差共分散を評価する方法）。
iminuit を用いたフィット（MIGRADアルゴリズムで最小化を行い、HESSEによる共分散評価とMINOSによる信頼区間推定を行う方法）。

比較のポイントは以下の3点です:

最小化アルゴリズムの違い（アルゴリズムの構造・更新則・数理的背景）
共分散評価の違い（どんな前提で、どうやって誤差共分散行列を構成するか）
信頼区間評価の違い（対称誤差 vs 非対称誤差の定義と意味、その数式的導出）

各手法について、理論的背景を数式と共に説明しつつ、対応するPythonコード例（fit_least_squares関数、fit_minuit関数など）を示します。また、pinv（疑似逆行列）を使うことで数値計算上の安定性が増す理由や、MINOS法で非対称誤差が得られることの意義について、物理計測（例: スペクトルのピークフィット）の観点からわかりやすく解説します。最後に、どの手法をどんな条件で選ぶべきかというガイドラインをまとめます。

この記事の実行例は google colab にも置いています。

とりあえず、使ってみたいという方は、

の記事から読んでください。

1. SciPy `optimize.least_squares` を用いた最小二乗フィット

1.1 最小化アルゴリズムの概要 (Levenberg-Marquardt法と信頼領域法)

SciPyの optimize.least_squares 関数は、非線形最小二乗問題を解くための高水準関数です。残差ベクトル $\mathbf{f}(x)$（観測値とモデルの差の集合）を最小化するパラメータ $x$ を見つけるもので、既定では以下のアルゴリズムを選択できます:

Levenberg-Marquardt法 (method='lm') – 古典的なガウス＝ニュートン法を拡張した手法で、小規模で制約のない問題に効率的です。ヤコビアンの近似に基づき、ヘッセ行列(二階微分の行列)の近似である $J^T J$（$J$はヤコビアン）にダンピング項$\lambda I$を加えて方程式を解き、反復的に解に近づきます（$ (J^T J + \lambda I)\Delta x = -J^T f $ の形でステップ $\Delta x$ を計算）。$\lambda$は各反復で調整され、ガウス-ニュートン法（$\lambda$小）と最急降下法（$\lambda$大）の中間として振る舞います。**MINPACK**ライブラリの実装が利用されており、高エラー次元の問題でも収束性に優れています。
信頼領域反射法 (method='trf') – デフォルトの手法です。現在の推定解の周囲に信頼領域（ステップの大きさを制限する領域）を設定し、その中で二次近似問題を解くアルゴリズムです。逐次的に信頼領域を調整しながら解を探索し、パラメータに上下限があっても安定に動作します。内部ではガウス＝ニュートン法やdogleg法を組み合わせつつ、大きすぎるステップは縮小されます。
Dogleg法 (method='dogbox') – 小規模問題向けの信頼領域アルゴリズムです。ガウス–ニュートンのステップと勾配降下のステップを組み合わせ（doglegパス）、矩形の信頼領域内で最適ステップを見つけます。ヤコビアンがランク落ちするような問題には非推奨ですが、小さい問題で高速。

SciPyはヤコビアン行列 $J_{ij} = \partial f_i/\partial x_j$ を用いており、jacオプションでユーザーがヤコビアン関数を与えない場合、自動的に有限差分で数値計算します。LM法では $J^T J$ が目的関数のヘッセ行列の近似となるため（ガウス＝ニュートン近似）、これを利用して高速に最小化が進みます。一方、trf/dogbox法では疎行列や巨大問題にも対応できるよう工夫されています。いずれの場合も、収束判定には勾配ノルムやステップ変化量などの基準が設定されています。

まとめると: SciPyのアルゴリズムは数値勾配と近似ヘッセ行列（ヤコビアン）を駆使したニュートン系手法です。LM法はパラメータ数が少なく制約なしの場合に非常に高速で、「半二乗法」とも呼ばれるくらい標準的です。一方TRF（信頼領域法）はよりロバストで、パラメータに制約（bounds）のある場合やヤコビアンが巨大な場合にも適用可能です。これらは基本的に二乗和が放物面状（二次関数的）であると仮定して局所解を探すため、問題が線形に近いほど効率良く正確に動作します。

1.2 共分散行列による誤差評価 (`inv` vs `pinv`)

SciPyの least_squares（およびこれを内部で用いるcurve_fit）では、フィット後にパラメータの推定誤差を評価するために誤差共分散行列を利用します。最適化結果 res から得られるヤコビアン $J$（最適パラメータにおける偏微分の行列）を用いて、近似ヘッセ行列は $H \approx J^T J$ とみなせます。ここで各要素 $(H)_{jk} = \sum_i (\partial f_i/\partial p_j)(\partial f_i/\partial p_k)$であり、これは目的関数（$\chi^2$など）のヘッセ行列の近似になっています。誤差共分散行列 $C$ はこの逆行列で与えられます:

$C \approx (J^T J)^{-1} \tag{1}$

これはフィットパラメータの推定誤差の分散を表し、対角成分$\sqrt{C_{jj}}$がパラメータ$j$の標準誤差（1$\sigma$相当）となります。式(1)は近似的な線形理論に基づいており、フィットモデルが最適値付近で線形近似できる場合に有効です。実際、テイラー展開で残差 $f_i(p)$ を最適解 $p^{*}$ 周りで線形化すると $f_i(p) \approx f_i(p^*) + \sum_j J_{ij}(p_j - p^*_j)$となり、$\chi^2 = \sum_i f_i(p)^2$ の二次近似から上記の共分散が導かれます。言い換えると、十分なデータ点数とほぼ線形なモデルでは、この $(J^T J)^{-1}$ は漸近的に正しいパラメータ分散を与えます。

補足説明

前提条件

観測誤差が 正規分布（Gaussian） に従う場合、尤度関数は以下のように書ける：

$$
p(\boldsymbol{y} \mid \boldsymbol{\theta}) \propto \exp\left( -\frac{1}{2} \chi^2(\boldsymbol{\theta}) \right)
$$

ここで $\chi^2(\boldsymbol{\theta})$ は、残差ベクトル $\boldsymbol{r}(\boldsymbol{\theta}) = \boldsymbol{y} - \boldsymbol{f}(\boldsymbol{x}; \boldsymbol{\theta})$ に対する重み付き二乗和：

$$
\chi^2(\boldsymbol{\theta}) = \boldsymbol{r}^\top(\boldsymbol{\theta}), \boldsymbol{W}, \boldsymbol{r}(\boldsymbol{\theta})
$$

このように、$\chi^2$ を指数部に含めることで、パラメータ $\boldsymbol{\theta}$ に関する尤度関数が定義される。

$\chi^2$の形がガウス分布の指数部と同形であると言われますが、その理由は、以下のような段階的な議論を経て成立します：

[1] $\chi^2$ のテイラー展開（最適推定値の近傍）

最小値 $\boldsymbol{\theta}_\mathrm{opt}$ の近傍で $\chi^2$ を二次展開すると：

\chi^2(\boldsymbol{\theta}) \approx \chi^2_\mathrm{min} + 
   (\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})^\top H\, 
   (\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})

ここで、$H = J^\top \boldsymbol{W} J$ はヤコビ行列によって構成されるヘッセ行列の近似である。

[2] この $\chi^2$ を使って定義された尤度関数

   p(\boldsymbol{y} \mid \boldsymbol{\theta}) \propto \exp\left( 
   -\frac{1}{2} \chi^2(\boldsymbol{\theta}) \right)

上記の二次近似を代入すると、指数部は以下のように書ける：

   -\frac{1}{2} (\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})^\top H 
   (\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})

これは、多変量正規分布の指数部と同じ構造を持つ。

結論

したがって、$\chi^2$ の二次近似：

\chi^2(\boldsymbol{\theta}) \approx \chi^2_\mathrm{min} + 
(\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})^\top H 
(\boldsymbol{\theta} - \boldsymbol{\theta}_\mathrm{opt})

に基づいて定義される尤度関数は、次の形の正規分布に一致する：

$$
p(\boldsymbol{\theta} \mid \boldsymbol{y}) \approx \mathcal{N}(
\boldsymbol{\theta}_\mathrm{opt},, \Sigma), \quad \Sigma = H^{-1}
$$

すなわち、最小二乗法における推定値の周辺では、パラメータの事後分布は多変量正規分布に近似できる。このとき、分散共分散行列は $\Sigma = (J^\top \boldsymbol{W} J)^{-1}$ で与えられる。

しかし, $J^T J$ が特異または条件の悪い行列である場合には注意が必要です。ヤコビアンの列が強い相関を持つ（パラメータ間に冗長性がある）と、$J^T J$ はランク落ちする可能性があります。例えば過剰なパラメータを含むモデルでは、データで一意に決まらない組み合わせが存在し、行列が ill-posed (不良設定問題)になります。このような場合、直接の逆行列計算 (np.linalg.inv) は数値的不安定や$\infty$の出力を招きます。実際にSciPyのLM法では、解のヤコビアンがフルランクでないと推定共分散行列を inf 埋めで返す仕様になっています。一方でSciPyのTRFやdogbox法では、Moore-Penroseの疑似逆行列（numpy.linalg.pinv）が内部で用いられ、安定的に共分散を計算しています。疑似逆行列はSVD（Singular value decomposition:特異値分解）を使って小さすぎる特異値を0に扱うため、完全な逆行列が存在しない場合でも最小二乗解に対応する共分散を与えてくれます。これにより、極めて不安定な方向には巨大な分散（不確かさ）を示すことで「このパラメータは実質決まらない」ことを示しつつ、計算自体は破綻しないという利点があります。例えば、SciPyのcurve_fitでは共分散行列の条件数（$\kappa$）が大きい場合は結果が不安定である警告をユーザに与えています。実務上も、np.linalg.cond(pcov) を計算してみて非常に大きければ、フィット結果の信頼性に注意が必要です。

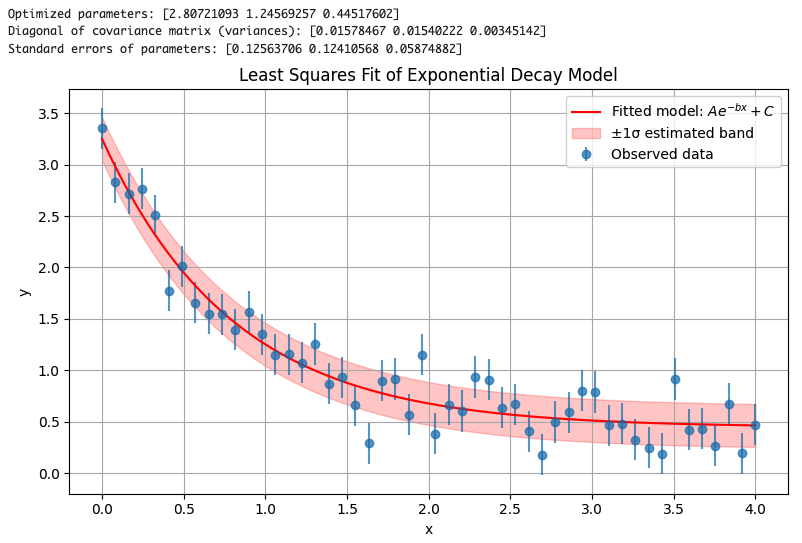
Python実装例: SciPyを用いた最小二乗フィットと共分散計算のコードは以下のようになります（簡単な指数関数モデルを例とします）:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import least_squares

# --- Model function ---
def model(x, A, b, C):
    return A * np.exp(-b * x) + C

# --- Residual function ---
def residuals(params, x, y):
    A, b, C = params
    return model(x, A, b, C) - y

# --- Generate synthetic data ---
np.random.seed(0)
xdata = np.linspace(0, 4, 50)
true_params = [2.5, 1.3, 0.5]
y_true = model(xdata, *true_params)
noise = 0.2 * np.random.randn(xdata.size)
ydata = y_true + noise

# --- Initial guess and fitting ---
initial_guess = [1.0, 1.0, 0.0]
res = least_squares(residuals, initial_guess, args=(xdata, ydata))
popt = res.x

# --- Covariance estimation ---
J = res.jac
residual_variance = 2 * res.cost / (len(ydata) - len(popt))  # res.cost is 0.5 * sum(residual^2)
cov = np.linalg.pinv(J.T @ J) * residual_variance
perr = np.sqrt(np.diag(cov))  # Standard errors

# --- Output results ---
print("Optimized parameters:", popt)
print("Diagonal of covariance matrix (variances):", np.diag(cov))
print("Standard errors of parameters:", perr)

# --- Visualization ---
xfit = np.linspace(0, 4, 200)
yfit = model(xfit, *popt)

# Simple ±1σ estimate using residual standard deviation (for illustration)
resid_std = np.std(ydata - model(xdata, *popt))
yfit_upper = yfit + resid_std
yfit_lower = yfit - resid_std

plt.figure(figsize=(8, 5))
plt.errorbar(xdata, ydata, yerr=0.2, fmt='o', label="Observed data", alpha=0.7)
plt.plot(xfit, yfit, 'r-', label="Fitted model: $A e^{-bx} + C$")
plt.fill_between(xfit, yfit_lower, yfit_upper, color='red', alpha=0.2, label="±1σ estimated band")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Least Squares Fit of Exponential Decay Model")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

上記のコードでは、least_squares による最小二乗フィッティングの結果からヤコビ行列 J を取得し、その近似的なヘッセ行列 $J^\top J$ を使ってパラメータの共分散行列を推定しています。これは、パラメータ空間における目的関数（残差の二乗和）の曲率を反映するものです。

ただし、least_squares に観測値の誤差（標準偏差）を明示的に渡していない場合、共分散行列のスケール（全体的な大きさ）が定まりません。このため、残差のばらつき（分散）を別途見積もる必要があります。

そこで、目的関数の値 res.cost（これは残差二乗和の半分）を用いて、残差の不偏分散を以下の式で推定します：

$$
\sigma^2 \approx \frac{\text{RSS}}{N - n}
$$

ここで、RSS（Residual Sum of Squares）は $2 \times \text{res.cost}$、$N$ はデータ点数、$n$ は推定パラメータの数です。

このスケーリングにより、パラメータの分散推定が妥当な値となり、共分散行列に意味を持たせることができます。

なお、これは SciPy の curve_fit 関数でも同様に行われており、absolute_sigma=False（デフォルト）の場合には、自動的にこのスケーリングが適用され、Reduced カイ二乗（reduced chi-squared）が1になるように共分散行列が調整されます。

1.3 共分散行列に基づく信頼区間評価（対称誤差の意味）

SciPyで得られる誤差共分散行列から計算される不確かさ（標準誤差）は、対称な誤差幅を意味します。例えば上記のフィット結果に対し、あるパラメータ$p_j$の推定値$\hat{p_j}$に対する1$\sigma$誤差が$\Delta p_j$であれば、信頼区間は $\hat{p_j} \pm \Delta p_j$ と対称になります。これは以下の仮定に基づきます:

二次近似（正規近似）: フィットの目的関数（例えば$\chi^2$や対数尤度）が最良解付近で放物線状の形状をしている（すなわち2次の項で支配され高次の非線形項が無視できる）こと。
大数の法則的な近似: データ点数が十分大きく、残差が（真のパラメータ付近で）正規分布に従うこと。

この条件下では、推定された共分散行列$C$により「真の値がその範囲に含まれる確率が68%（1$\sigma$）」となる区間が計算できます。たとえば、目的関数が $\chi^2$ であれば、真のパラメータ値との差による$\chi^2$の増加は近似的に二次形式で表されます:

$$
\chi^2(p) \approx \chi^2_{\min} + \frac{1}{2}(p - \hat{p})^T H (p - \hat{p})
$$

ここで$H = J^T J$はヘッセ行列の近似です。1パラメータの場合、これは放物線 $\chi^2(p) \approx \chi^2_{\min} + \frac{1}{2}H (p-\hat{p})^2$ となり、$\Delta\chi^2 = 1$ 上昇する点を求めると $(p-\hat{p})^2 = \frac{2 \cdot 1}{H}$ となります。したがって $p$ の標準誤差 $\sigma_p = \sqrt{\frac{2}{H}} = \sqrt{(H^{-1})}$ となり、これは先述の$C=(J^T J)^{-1}$の対角要素の平方根に一致します。一般に$n$パラメータの場合でも、共分散行列$C$の対角成分$\sqrt{C_{jj}}$を1$\sigma$誤差と解釈できます。複数パラメータがある場合、任意の一つを動かしたときの$\Delta\chi^2=1$条件は他のパラメータ固定か他パラメータも変動許可かで意味が異なりますが、通常共分散行列から得る誤差は他パラメータも調整された場合の一パラメータ辺りの標準誤差（いわゆる母数誤差）を指しています。この意味では、SciPyで計算する対角要素からの誤差$\Delta p_j$は、他のパラメータが最適値から動かないと仮定した微小変化と近似的に等価ですが、線形近似の範囲では同時信頼区間の一部とも解釈できます。

重要な点: 対称誤差はあくまで近似的指標です。モデルが非線形であったり、パラメータ空間で目的関数が歪な形状をしている場合、真の信頼区間は対称ではなくなることがあります（例えば「下側には余裕があるが上側にはほとんど余裕がない」ような場合）。そのような場合でも、SciPyの方法では対称な$\pm1\sigma$しか提供されません。これは測定誤差が大きい場合や、パラメータに物理的な下限（例: 強度は0未満にならない等）がある場合によく起こります。スペクトルのピークフィットなど物理測定の例では、あるピークの面積（強度）がゼロに近いとき、負の方向の不確かさは物理的に制限され（0以下にはならない）、正の方向には大きな不確かさを持つ、といった非対称誤差が考えられます。しかしSciPyの共分散評価ではその非対称性は反映されず、「仮に正規近似できれば」という前提での誤差評価となります。後述するMINOS法ではこの問題に対応できますが、SciPyのみで非対称の信頼区間を求めるにはプロファイル尤度法等を自前で実装してスキャンする必要があります。

以上がSciPyのフィット手法における最小化アルゴリズム、共分散による誤差評価、及び信頼区間の扱いです。次に、物理学分野で広く使われているMINUITアルゴリズム（Python実装であるiminuit）を用いた手法を見ていきましょう。

2. iminuit (Minuit) を用いたフィットと誤差推定

高エネルギー物理分野などで伝統的によく使われてきたMINUITは、CERNで開発された汎用の関数最小化&エラー分析ツールです。Pythonからはiminuitライブラリとして利用でき、同様に最小二乗法や尤度法でのフィットに強力な機能を発揮します。本節では、MinuitのMIGRADアルゴリズム（最小化）、HESSE（共分散計算）、MINOS（信頼区間計算）について解説します。

2.1 最小化アルゴリズム MIGRAD の概要 (変量メトリック法)

Minuitのデフォルト最適化ルーチンであるMIGRADは、40年以上にわたり実績のある強力な最小化アルゴリズムです。に示されるように、MIGRADはDavidon-Fletcher-Powell (DFP)法に代表される変量メトリック法（準ニュートン法）の一種で、勾配ベクトルと関数値の情報からヘッセ行列（の逆行列）の近似を逐次更新しつつ極値を探索します。簡単に言えば、一階導関数（勾配） を用いてニュートン法的な二次収束性を目指す手法です。MIGRADの特徴をまとめると:

最適化アルゴリズムの中には、パラメータの誤差共分散行列（あるいは目的関数のヘッセ行列の逆行列）を近似行列として内部的に持ち、これを逐次更新しながら最適解を求めていく手法があります。初期状態では、たとえば単位行列のような単純な行列を近似共分散行列として用い、各ステップでの勾配の変化 $\Delta g = g_{k+1} - g_k$ と、パラメータの変化 $\Delta x = x_{k+1} - x_k$ に基づいて、この行列を更新します。このような手法の代表例が BFGS法（Broyden–Fletcher–Goldfarb–Shanno） や DFP法（Davidon–Fletcher–Powell） です。どちらも 準ニュートン法（quasi-Newton methods） に分類され、ヘッセ行列（またはその逆行列）を直接計算せずに、信頼できる近似行列を段階的に洗練していく特徴を持ちます。これにより、各ステップで二階微分（ヘッセ行列）を計算するコストを省きつつ、ニュートン法に近い高速な収束性を実現できます。
ステップの方向は、この推定誤差行列が与えるNewtonステップに沿うのが理想ですが、開始直後は近似が粗いため最急降下方向（勾配方向）に近い動きもします。Minuitでは「strategy」というパラメータで初期ヘッセ行列の扱いやステップ計算の慎重さを調整できますが、通常は最初に一度HESSEを呼び出して初期誤差行列を計算するのがデフォルトです。
収束判定にはEDM (estimated distance to minimum)という基準が使われます。これは現在の勾配と誤差行列から推定される「あとどれくらい$\chi^2$が下がる余地があるか」という指標で、これが十分小さくなると収束とみなされます。MIGRADは勾配が必要ですが、ユーザがコスト関数を与えるだけで内部で自動微分または有限差分により勾配を計算してくれます。

MIGRADの利点は、高度に最適化されたC++実装（Minuit2ライブラリ）により高速かつ堅牢に動作することです。また、準ニュートン法ゆえ、大域的最小値に到達する保証はありませんが十分な初期値を与えれば局所収束が非常に速いです。SciPyのLM法との違いは、MIGRADは一般のコスト関数（必ずしも二乗和形式でなくてもOK）を扱える点です。例えば最尤法の $-2\ln L$ などもErrordefさえ適切に設定すれば最小化できます。一方でSciPyのleast_squaresは二乗和形式専用に最適化されているため、同じ問題設定（非線形最小二乗）であればSciPyもMinuitも類似の結果が得られることが多いです。

MIGRADの弱点もわずかにあります。それは誤差行列の収束評価です。MIGRADは最小化と同時に誤差行列も更新していますが、その推定は完全ではない場合があります。特に以下のケースで注意が必要です:

極小値への収束が速すぎた場合: 十分な反復回数が稼げず、誤差行列（共分散）の推定が粗い可能性があります。そのような場合Minuitは自動でHESSEを呼び追加計算することがあります。少ない関数呼び出しで収束したときは誤差を過信しないようにとの警告が出ることもあります。
問題が強非線形な場合: 勾配が位置によって大きく変わるような非線形では、MIGRAD中で構築した誤差行列が「平均化された」ものになってしまい、真のヘッセ行列とは異なることがあります。この場合、たとえ十分反復してもMIGRAD内蔵の誤差行列は信用できず、後述のMINOS法でないと正確な区間は得られません。

Minuitの開発者は「真剣に誤差評価をするなら、MIGRAD収束後に必ずHESSEを呼ぶべし」と助言しています。実際、多くの解析では m.migrad() 後に m.hesse() を呼び、HESSE計算による確定的な共分散行列を取得します。

2.2 HESSEによる共分散評価（ヘッセ行列の直接計算）

HESSEはMinuitにおける誤差共分散行列の計算ルーチンです。m.hesse()を呼ぶことで現在の最良パラメータ点における実際のヘッセ行列（二階微分行列）を数値的に計算し、その逆行列を求めます。具体的には、各パラメータについて目的関数$F$（例えば$\chi^2$）の二階偏導関数 $\partial^2 F/\partial p_i \partial p_j$ を有限差分で評価し、行列$H$を組み立て、これを逆行列演算します。HESSEで得られる共分散行列（Minuitでは「エラーマトリックス」と呼称）は、SciPyで前述した $ (J^T J)^{-1}$ に相当するものです。ただしMinuitの場合、errordefという設定値に基づきエラーマトリックスをスケールします。最小二乗（$\chi^2$）の場合は通常 errordef=1（$\Delta \chi^2=1$が1$\sigma$区間）を指定します。HESSEの結果はMinuitオブジェクトの m.covariance プロパティや m.errors（各パラメータの1$\sigma$誤差の辞書）で取得できます。

HESSEによる共分散評価の前提も、基本的にはSciPyの場合と同様です:

ヘッセ行列が正定である（＝極小解であること）。Minuitは非物理的な状況でヘッセ行列が負定または縮退すると警告を出したり、自動で微小な補正を加えて正定にします。極小点では理論上ヘッセ行列は正定（全ての固有値が正）でなければなりません。
パラメータ間の相関も考慮されます。MinuitはHESSE計算後に相関行列も表示できますし、対角成分が標準誤差、非対角成分がパラメータ間の共分散を含む行列自体も取得できます。相関係数が1または-1に極端に近い場合、そのパラメータは 過剰（冗長） でデータでは固有に決まらない可能性が示唆されます。この点もSciPyと同様で、共分散行列の条件数や相関を見ることでフィットの質を判断できます。

HESSEの利点は、現在の点の微小変化に基づく線形近似上の誤差を厳密に計算するため、SciPyでの共分散計算と同等の結果が得られることです。MIGRAD直後にHESSEを呼ぶことで、MIGRAD中に蓄積したエラーマトリックスの不確かさを払拭し、最新の曲率に基づく誤差が算出されます。多くの場合、このHESSE由来の対称誤差は十分有用で、物理解析でもまずは対称誤差として報告されることが多いです。Minuitではm.migrad(); m.hesse()後の m.errors がSciPyの対称誤差と同義と考えてよいでしょう。

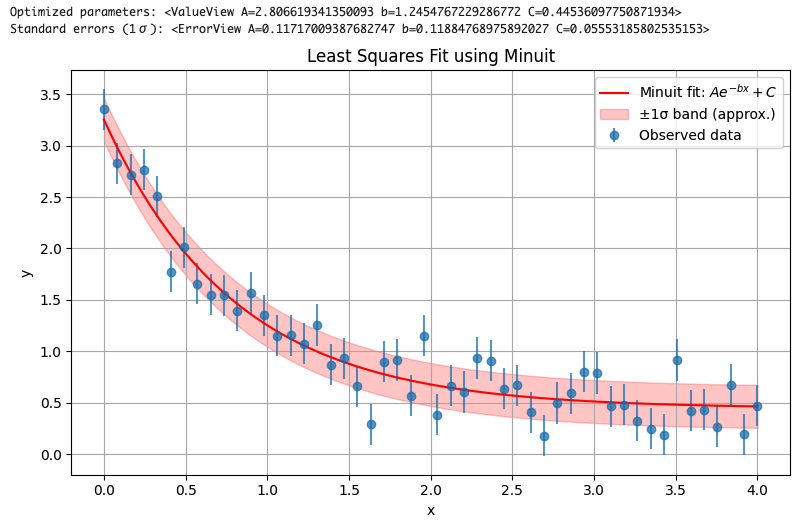
Pythonでのiminuit使用例: 先ほどの指数関数フィットをiminuitで行ってみます。Chi-square関数を定義し、それをMinuitに渡してMIGRAD→HESSEを実行します:

fit_iminuit.py

import numpy as np
import matplotlib.pyplot as plt
from iminuit import Minuit

# --- Define model: exponential decay ---
def model(x, A, b, C):
    return A * np.exp(-b * x) + C

# --- Generate synthetic data ---
np.random.seed(0)
xdata = np.linspace(0, 4, 50)
true_params = [2.5, 1.3, 0.5]
y_true = model(xdata, *true_params)
noise = 0.2 * np.random.randn(len(xdata))
ydata = y_true + noise
sigma = 0.2  # Assumed constant Gaussian noise

# --- Define chi-square function for Minuit ---
def chi2(A, b, C):
    residuals = model(xdata, A, b, C) - ydata
    return np.sum((residuals / sigma)**2)

# --- Initialize and run Minuit ---
m = Minuit(chi2, A=1.0, b=1.0, C=0.0)
m.errordef = 1.0  # For chi-squared minimization
m.migrad()        # Run minimization
m.hesse()         # Compute covariance matrix

# --- Extract fit result and uncertainties ---
popt = m.values
perr = m.errors

print("Optimized parameters:", popt)
print("Standard errors (1σ):", perr)

# --- Visualization ---
xfit = np.linspace(0, 4, 200)
yfit = model(xfit, *popt)

# Simple ±1σ error band using residual standard deviation (for illustration)
resid_std = np.std(ydata - model(xdata, *popt))
yfit_upper = yfit + resid_std
yfit_lower = yfit - resid_std

plt.figure(figsize=(8, 5))
plt.errorbar(xdata, ydata, yerr=sigma, fmt='o', label="Observed data", alpha=0.7)
plt.plot(xfit, yfit, 'r-', label="Minuit fit: $A e^{-bx} + C$")
plt.fill_between(xfit, yfit_lower, yfit_upper, color='red', alpha=0.2, label="±1σ band (approx.)")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Least Squares Fit using Minuit")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

MIGRADが正常終了すれば、m.migrad()の戻り値である Minuit オブジェクトには m.fval (最小化されたコスト値), m.values (パラメータ推定値のリスト/辞書), m.errors (対称誤差のリスト/辞書) といった情報が入っています。また m.covariance で誤差共分散行列 (オブジェクト形式)も取得できます。例えば m.covariance[(\"A\",\"b\")] のようにアクセスすればパラメータAとbの共分散要素が得られます。

2.3 MINOSによる信頼区間評価（非対称誤差の意義）

Minuitが他のフィッティングライブラリと一線を画する大きな特徴がMINOS法による信頼区間（エラー帯）評価です。MINOSは、前述のHESSE法とは異なり非線形性を考慮した精密な誤差推定手法であり、多くの場合非対称な誤差幅を与えます。その基本アイデアは、「放物線と仮定せずに実際の目的関数が最小値からどれだけ上昇したら有意かを調べ、その際のパラメータ変化量を求める」ことです。具体的な手順は以下のようになります:

あるパラメータ $p_j$ について、一方の方向（プラス側）に向けて値を増やしていきます。他のパラメータは、その都度最適化し直し（プロフィール尤度法）、全体の最小値条件を保ちながら $p_j$ が固定値になったときの目的関数値$F(p_j^{\text{fix}})$を求めます。
$F$（例えば$\chi^2$）が最小値 $F_{\min}$から所定の値だけ増加するところでストップします。その所定の増加量がMinuitでは errordef（またはUP値）で、たとえば$\chi^2$フィットでは1.0を設定すれば「$\Delta\chi^2 = 1$上昇する点」を探すことになります。
発見した点の $p_j$ 値を $p_{j}^{+}$ とすると、これが上側1$\sigma$境界です。同様にマイナス方向（値を減らす方向）にも探索し、$\Delta\chi^2 = 1$上昇する点の $p_j^{-}$ を見つけます。
こうして $p_j$ の最良推定値 $\hat{p_j}$に対するプラス側誤差 $\sigma_{j}^{+} = p_j^{+} - \hat{p_j}$、マイナス側誤差 $\sigma_{j}^{-} = \hat{p_j} - p_j^{-}$ が得られます。

この方法により得られる区間 $[\hat{p_j} - \sigma_j^{-}, \hat{p_j} + \sigma_j^{+}]$ には、原理的には真の値が約68%の確率で含まれる（1標準偏差に相当）ことが保証されます。重要なのは、この区間は一般に非対称となりうることです。典型的には、HESSEの対称誤差$\sigma_{j,\text{HESSE}}$はこの非対称区間の上下の誤差の中間くらいになります。すなわち多くの場合、

$\sigma_j^{-} < \sigma_{j,\text{HESSE}} < \sigma_j^{+}$

という関係になり、3つの値の差がその問題の非線形性の強さを反映します。完全に線形であれば3つは等しくなり、非線形性が強いと差が大きくなります。

物理計測の視点から、MINOSの利用頻度は多いです。例えばスペクトル中のピークフィットでバックグランドが高い中に埋もれた微かなピークをフィットしたとしましょう。ピーク強度の最良値がゼロに近い場合、実際には「0にもなり得るし正の値にもなり得る」状況で、誤差は大きく非対称になるはずです（上側には大きく、下側にはほぼゼロまで）。HESSEの対称誤差ではこの状況を正確に表せず、誤差の意味を誤解するかもしれません。しかしMINOSは真に68%信頼で含まれる範囲を直接求めるため、下限側は0まで（$\sigma^{-} \approx \hat{p}$）、上限側は大きな値まで（$\sigma^{+} \gg \sigma^{-}$）という形で出力されます。この情報は実験家にとって「このピーク強度は上方向にはこれだけ大きくなり得るが、下方向にはほぼゼロまで不確かだ」という定性的な理解を与えてくれます。単に「$\sigma$ = 5だ」という対称誤差だけでは見逃してしまう可能性のある事実を、MINOSはあぶり出してくれるのです。

Minuit (iminuit)でMINOSを使うのは簡単で、m.minos() を呼ぶだけです。先のコード例に続けて:

m.minos()  # MINOS法での誤差解析
print("非対称誤差:", m.merrors)  # MinosErrorオブジェクト (辞書) として各パラメータに存在

とすれば、m.merrors に各パラメータの MinosError が格納されます。例えば m.merrors['A'].upper と m.merrors['A'].lower にそれぞれ $\sigma_A^{+}$, $\sigma_A^{-}$が入っています。Minuitは内部で賢く探索範囲を広げたり縮めたりしつつ、できるだけ少ない関数評価回数で目的の$\Delta F$上昇点を見つける工夫がされています。ただし多次元パラメータの場合、MINOS誤差の計算コストはパラメータ数にも比例して増えます（各パラメータについて最小化を繰り返すため）。それでも、最も信頼できる誤差推定として物理解析ではMINOSが標準とされています。

fit_minos.py

import numpy as np
import matplotlib.pyplot as plt
from iminuit import Minuit

# --- Model function ---
def model(x, A, b, C):
    return A * np.exp(-b * x) + C

# --- Generate synthetic data ---
np.random.seed(0)
xdata = np.linspace(0, 4, 50)
true_params = [2.5, 1.3, 0.5]
y_true = model(xdata, *true_params)
noise = 0.2 * np.random.randn(len(xdata))
ydata = y_true + noise
sigma = 0.2  # assumed constant noise

# --- Chi-square function ---
def chi2(A, b, C):
    residuals = model(xdata, A, b, C) - ydata
    return np.sum((residuals / sigma) ** 2)

# --- Minimization and error analysis ---
m = Minuit(chi2, A=1.0, b=1.0, C=0.0)
m.errordef = 1.0
m.migrad()
m.hesse()     # symmetric errors
m.minos()     # asymmetric errors (Minos)

# --- Output results ---
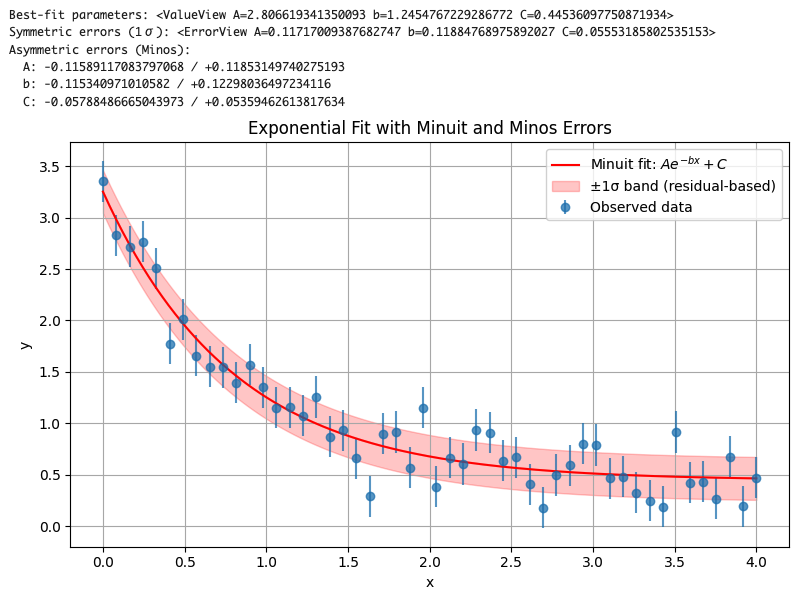
print("Best-fit parameters:", m.values)
print("Symmetric errors (1σ):", m.errors)
print("Asymmetric errors (Minos):")
for name in m.parameters:
    err = m.merrors[name]
    print(f"  {name}: -{abs(err.lower)} / +{abs(err.upper)}")

# --- Visualization ---
xfit = np.linspace(0, 4, 200)
yfit = model(xfit, *m.values)  # unpack ValueView directly

# Simple ±1σ band (residual-based, not from Minos)
resid_std = np.std(ydata - model(xdata, *m.values))
yfit_upper = yfit + resid_std
yfit_lower = yfit - resid_std

plt.figure(figsize=(8, 5))
plt.errorbar(xdata, ydata, yerr=sigma, fmt='o', label="Observed data", alpha=0.7)
plt.plot(xfit, yfit, 'r-', label="Minuit fit: $A e^{-bx} + C$")
plt.fill_between(xfit, yfit_lower, yfit_upper, color='red', alpha=0.2, label="±1σ band (residual-based)")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Exponential Fit with Minuit and Minos Errors")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

最後に、MinuitのHESSEとMINOSの結果の関係について補足します。Minuitのドキュメントにも「MinosとHesseの結果がほぼ一致しているなら、その誤差は妥当である可能性が高い」旨の記述があります。実際、よほどの非線形でなければMINOSの上下誤差はHESSEの対称誤差と大差ない場合も多々あります。しかし万が一の非線形を見逃さないため、特に重要なパラメータについてはMINOSを確認することが推奨されます。

3. 手法の比較と使い分けガイドライン

以上、SciPyのleast_squaresによる方法と、Minuitによる方法を詳細に見てきました。それぞれのメリット・デメリットを整理し、どのような状況でどちらを選択すべきかの指針を示します。

アルゴリズムの特性:
- SciPy (LM/TRF): 非線形最小二乗専用の実装で、ヤコビアンを利用した効率の良いステップ計算を行います。実装が純Python＋NumPyで手軽に使え、簡単なモデルなら数行でフィットできます。勾配計算も自動で行われます。ただし一般のコスト関数には使えず、あくまで「残差」の二乗和を定義できる問題に限られます。また大域的探索機能はなく、初期値依存で局所解に陥る可能性はMinuit同様にあります。
- Minuit (MIGRAD): 勾配法ベースの汎用最適化であり、二乗和に限らず任意の目的関数を扱えます。C++由来の高速性と40年の改良で極めて頑健に動作します。ただしPythonから使うにはiminuitのインストールが必要で、関数の書き方（引数を個別にとる必要があるなど）に若干の制約があります。自動微分は無く有限差分に頼る点はSciPyと同様ですが、戦略パラメータによっては探索に時間がかかることもあります。
誤差共分散の評価:
- SciPy: フィット結果から自前でヤコビアンを使い $(J^T J)^{-1}$を計算する必要があります（curve_fitを使った場合は自動でpcovが返りますが、least_squares単体では返り値に含まれません）。その際、行列の状態によっては np.linalg.inv よりも np.linalg.pinv を使う方が安全です。共分散行列が得られれば、パラメータ間の相関や不確かさを評価できます。ただし、これらは線形近似に基づくため、信頼区間の厳密さは保証されません。
- Minuit: m.hesse() により一発で共分散行列を計算できます。Minuitは元々誤差評価込みで設計されており、収束判定や行列の正定性チェックなども組み込まれているため、ユーザは深く意識せずとも適切なエラーマトリックスを得やすいです。またMinuitはフィット失敗時には共分散が計算できない旨のエラーや警告（Failed to invert Hessian matrix等）を出しますので、フィットが不安定かどうかの判断が付きやすいです。
信頼区間（不確かさ）の解釈:
- SciPy: デフォルトでは対称誤差しか提供されません。非線形効果で誤差が非対称になる可能性があっても、それを自動では検知できません。ユーザが自分でパラメータを振ってみて、目的関数がどれだけ悪化するかを調べないと非対称性は評価できません。したがって、もし**「この誤差は対称とみなして良いのか？」**という疑問がある場合は、Minuitを使うか自前でのプロファイルスキャンが必要になります。
- Minuit: MINOS法による非対称誤差を簡単に得られます。非対称な場合その事自体が解析結果として重要な意味を持つことがあります。例えば上記のピーク強度の例では「負方向には0まで触れる」という事実は物理的にも意味深いです。このようにMinuitは統計的な信頼区間を直接的に与えてくれるため、結果の解釈を誤りにくいという利点があります。もっとも、完全に線形な問題ではMinosとHesseは同等であり、その場合Minosは計算コストが無駄にかかるだけとも言えます。
計算コストと安定性:
- SciPyのLM法は小規模問題では非常に高速ですが、パラメータが多かったりヤコビアン計算が重い場合、trust-region法で細かくステップを刻むぶん時間がかかることもあります。Minuitも同程度の反復を要しますが、C++実装ゆえPythonの関数呼び出しやデータ管理のオーバーヘッドが低く抑えられています。大量のデータ点を扱う場合、SciPyは内部でヤコビアン（m×n行列）の計算と因子分解をPythonで行うためメモリ面・速度面で制約があります。一方Minuitはユーザ関数（コスト計算）がPython実装である限りそこがボトルネックになりますが、並列化はユーザ側でMPIやマルチスレッドを組む必要があります（SciPyも同様）。
- 安定性という観点では、SciPyのLMはしばしば初期値によっては発散・振動するケースがあります。Minuitも初期値依存はありますが、ライン検索的なステップ調整やsimplex法へのフォールバック（migrad(..., use_simplex=True)で有効化可能）など収束を助ける工夫が多いため、困難な状況でも何とか収束点を探り当ててくれる印象があります。実際、MIGRADは「高エネルギー物理の複雑なフィット問題でもまずこれを使えば間違いない」と言われるほど定評があります。

以上を踏まえて、推奨ガイドラインをまとめます。

どちらの手法を使うべきか？ 次のチェックリストを参考にしてください:

フィットの目的が単純な最小二乗で、データ点数も十分多く近似的線形と考えられる場合：
→ SciPyのleast_squaresで十分。手軽で速く、Jupyter環境でも使いやすいです。パラメータ誤差も線形近似で問題なければ、curve_fitの出力pcovや自前計算の共分散から得た値で足ります。
パラメータ間の相関が強そう、もしくはモデルが非線形で誤差が歪む懸念がある場合：
→ Minuitを検討してください。特に精密に誤差評価する必要がある研究では、MINOSによる区間推定は信頼性が高いです。SciPyでフィットした後でも、重要パラメータだけMinuitで再フィットしてMINOS誤差を確認するといった併用も有効です。
制約条件や外れ値の扱いなど特殊な事情がある場合：
SciPyのleast_squaresは簡単にパラメータの範囲制限を付けられ、またロバスト損失関数（soft-l1やHuber関数等）もオプションで選べます。一方Minuit自体は単純な箱型制約のみサポート（パラメータを固定したり上下限をつけることは可能）で、外れ値対策はユーザーがコスト関数に組み込む必要があります。目的に応じて、SciPyの柔軟さとMinuitの高度なエラー解析を使い分けましょう。
計算資源と速度:
ごく大量のデータやパラメータの場合、どちらにせよ計算コストは高くなります。SciPyは大規模ではLMよりTRFを使うことでSVDではなく疎行列ソルバを使えますが、それでも限界はあります。Minuitは本質的に密なヘッセ行列を扱いますので高次元では時間がかかります。ただしMinuitのC++実装はマルチコア対応が内部でなされているため、ある程度は恩恵があります（iminuit 2.x系では並列化は限定的ですが、Minuit自体の効率でカバーしています）。総じて中規模までの問題では好みで、極めて大規模なら工夫が必要です。
学習・教育目的:
物理系の学生がこれらを学ぶ際、SciPyの実装は直接ニュートン法系の挙動を観察するのに適しています。一方Minuitはブラックボックス度が高いですが、エラー解析の統計的考え方（Hesse vs Minosの違いなど）を学ぶのに最適な実例となります。本記事の数式や引用も参考に、ぜひ両者を実際に使って挙動を比較してみてください。

おわりに

最小二乗フィッティング手法として、SciPyとMinuitという二つのアプローチを比較し、そのアルゴリズム的背景から誤差評価手法、信頼区間の解釈まで詳しく述べました。SciPyはPythonエコシステムで手軽に使える反面、結果の解釈はユーザ側の統計的理解に委ねられる部分があります。Minuit (iminuit)は一見とっつきにくいかもしれませんが、統計解析のベストプラクティスが凝縮された強力なツールです。物理系の解析においては、「フィットする」と「誤差を見積もる」は一対であり、その両方を正しく行ってはじめて科学的に意味のある結果が得られます。ぜひ目的に応じて両手法を使いこなし、堅実なデータ解析を行ってください。

X線天文学向けの補足

iminuit の minos() と XSPEC の error コマンドは、基本的に同じアルゴリズム的原理（MINOS法）に基づいています。

共通点：どちらも「MINOS法」による非対称誤差推定

目的：パラメータ推定値の上下における信頼区間（たとえば 68%、90%、95%）を、
- 「他のパラメータを再最適化しつつ」
- 「目的関数（$\chi^2$ や $-2 \log L$）がしきい値だけ増える点」
  を探して、上下の誤差を独立に評価します。
特徴：
- 非対称な誤差（下側と上側で幅が異なる）を評価できる
- 二次近似（ヘッセ行列）に依存しない → より信頼性が高い
- 他のパラメータと連動したカイ二乗地形の歪みも反映可能

相違点（実装面）

項目	`iminuit.minos()`	`XSPEC error`
実装	Python (`iminuit` C++ backend)	XSPEC (Fortran backend)
出力	`.merrors[name].lower/upper`	スクリーン表示（90% CI by default）
デフォルト信頼度	1$\sigma$（$\Delta \chi^2 = 1$）	90% confidence （$\Delta \chi^2 = 2.71$）
対応関数	任意の Python 関数	XSPEC model (spectrum-fitting)
並列処理	オプションで可能	多くは逐次的

注意点：信頼水準の違いに気をつける！

iminuit.minos() は errordef = 1.0（→ Δχ² = 1.0） ⇒ 1σ（68.3%）
XSPEC の error コマンドはデフォルトで $\Delta \chi^2 = 2.71$ ⇒ 90% 信頼区間

そのため、直接比較する際には、両者の $\Delta \chi^2$ を揃える必要があります。

参考文献・引用:

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up