はじめに
物理実験やスペクトル解析では、「ピーク位置」「幅」「強度」などをモデル関数にフィットして物理量を推定することが欠かせません。本記事では、Pythonを使って以下のステップでフィッティング処理を実装していきます:
- Scipy
least_squaresによる最小二乗フィッティング -
iminuitによる高精度なパラメータ推定 - 非対称誤差(MINOS)を用いた信頼区間の取得
- グラフとCSV出力による可視化と保存
最終的には、2本のガウスピーク+傾き付きバックグラウンドという典型的なスペクトル形状を対象に、擬似データを用いてフィッティングを行う例を紹介します。
実行環境は google Colab でも構築してますので、
の実行例を参考にしてください。
詳細な解説についてはこちらの記事を参考にしてください。
📦 使用ライブラリ(詳細)
pip install numpy matplotlib scipy pandas iminuit
上記のライブラリの中で、初心者には少しなじみが薄いが非常に強力なツールが iminuit です。
🔍 iminuit とは?
iminuit は、CERN(欧州原子核研究機構) によって長年使われてきた 最小化ライブラリ「Minuit(ミニュイ)」 を Python から使えるようにしたラッパーです。
- ✅ 最小化(関数の極小点探索) に特化したライブラリ
- ✅ 物理学や統計学の分野で実績があり、高精度・高信頼性
- ✅
scipy.optimizeよりも誤差評価に優れており、**非対称誤差(MINOSエラー)**が取得可能 - ✅ ユーザーが解析する パラメータ名が明示的に扱える(引数の名前で最適化できる)
🧠 名前の由来
-
Minuitはフランス語で「深夜(midnight)」を意味します。 - しかし、ライブラリの名前の由来は「Minimization Unit」の略とされることもあります(諸説あり)。
-
iminuitのiは Python interface(インターフェース) の意で、Minuitを Python で使えるようにしたバージョンです。
どんなときに使う?
- 実験データのフィッティングで「信頼区間が左右非対称」なとき
-
curve_fitやleast_squaresの誤差があいまいだと感じるとき - パラメータ同士の依存性(相関)をしっかり見たいとき
- 科学論文レベルの解析や精密なエラーバーが求められるとき
✅ 公式サイト
🧪 例:MINOS による非対称誤差の取得
m.migrad() # 最小化
m.hesse() # 共分散誤差
m.minos() # 上下非対称誤差(時間がかかるが精密)
これにより、非対称なパラメータの誤差推定が可能になります。
1️⃣ モデルの定義とデータ生成
まずは、2つのガウス関数と線形背景を持つモデルを定義し、それに基づいてノイズ付きのデータを生成します。
def model(x, p):
amp1, amp2, mu1, mu2, sigma, bkg0, bkg1 = p
return (
amp1 * np.exp(-0.5 * ((x - mu1) / sigma) ** 2) +
amp2 * np.exp(-0.5 * ((x - mu2) / sigma) ** 2) +
bkg0 + bkg1 * (x - 5870)
)
そしてデータ生成:
def generate_data(seed=42):
# 真のパラメータ
true_p = [10, 20, 5890, 5900, 2.0, 10, -0.1]
x = np.linspace(5870, 5920, 200)
y_true = model(x, true_p)
np.random.seed(seed)
y_obs = np.random.poisson(y_true)
y_err = np.sqrt(np.maximum(y_obs, 1))
return x, y_obs, y_err, y_true
2️⃣ Scipy によるフィッティング
Scipy の least_squares を使って最小二乗フィットを行います。
from scipy.optimize import least_squares
def fit_least_squares(x, y, yerr, init_p):
def residuals(p):
return (y - model(x, p)) / yerr
result = least_squares(residuals, init_p)
# 誤差計算
J = result.jac
sigma2 = np.sum(result.fun**2) / (len(y) - len(init_p))
cov = np.linalg.pinv(J.T @ J) * sigma2
return result.x, np.sqrt(np.diag(cov))
3️⃣ iminuit によるフィッティング(MINOS付き)
iminuit を用いることで、高度な誤差評価(非対称誤差も含む)が可能になります。
from iminuit import Minuit
from iminuit.util import describe
def fit_minuit_with_minos_asymmetric(x, y, yerr, init_p):
def chi2(amp1, amp2, mu1, mu2, sigma, bkg0, bkg1):
p = [amp1, amp2, mu1, mu2, sigma, bkg0, bkg1]
return np.sum(((y - model(x, p)) / yerr) ** 2)
param_names = describe(chi2)
m = Minuit(chi2, **dict(zip(param_names, init_p)))
m.errordef = Minuit.LEAST_SQUARES
m.migrad()
m.hesse()
m.minos()
values = [m.values[n] for n in param_names]
errs_lower = [m.merrors[n].lower if m.merrors[n].is_valid else np.nan for n in param_names]
errs_upper = [m.merrors[n].upper if m.merrors[n].is_valid else np.nan for n in param_names]
return param_names, values, errs_lower, errs_upper
4️⃣ 結果の可視化と保存
CSV形式で保存し、複数のフィット結果を比較するプロットも自動生成します。
def save_fit_result_csv_asymmetric(param_names, fit_name, values, err_low, err_high):
df = pd.DataFrame({
"Parameter": param_names,
f"{fit_name}_fit": values,
f"{fit_name}_err_lower": err_low,
f"{fit_name}_err_upper": err_high,
})
df.to_csv(f"fitresult_{fit_name}.csv", index=False)
print(df)
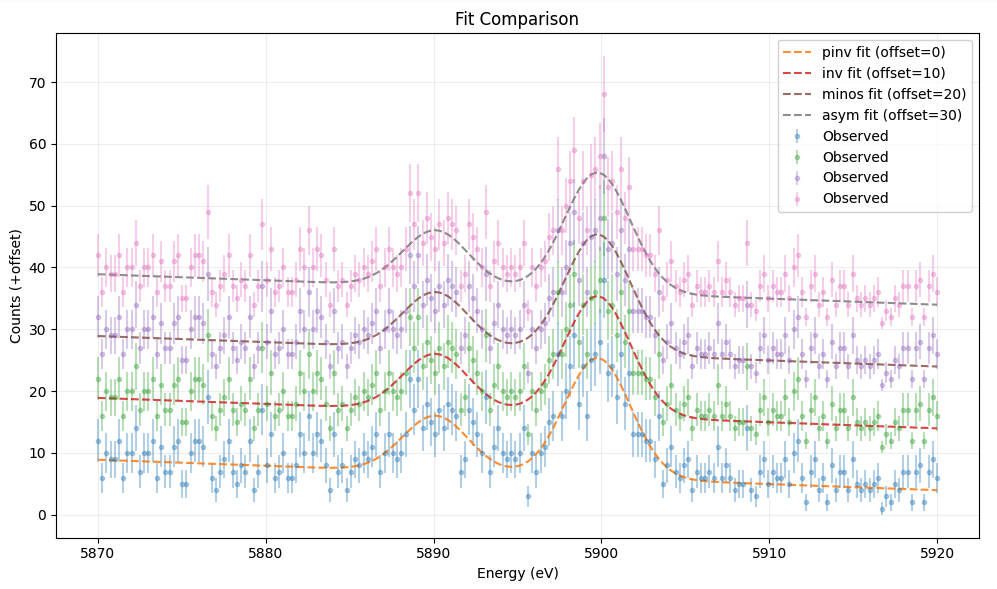
def plot_comparison(datafiles, offset_val=10):
plt.figure(figsize=(10, 6))
for i, fname in enumerate(datafiles):
df = pd.read_csv(fname)
offset = i * offset_val
plt.errorbar(df["x"], df["y_obs"] + offset, yerr=df["y_err"],
fmt='o', alpha=0.3, label=f"Observed + {offset}")
plt.plot(df["x"], df[df.columns[-1]] + offset, "--", label=f"Fit {i}")
plt.legend()
plt.xlabel("Energy (eV)")
plt.ylabel("Counts")
plt.title("Fit Comparison")
plt.grid(True, alpha=0.2)
plt.tight_layout()
plt.savefig("fit_comparison_all.png")
plt.show()
コード全文
# 必要なライブラリをインポート
import numpy as np # 数値計算ライブラリ
import matplotlib.pyplot as plt # グラフ描画ライブラリ
from scipy.optimize import least_squares # 最小二乗法によるフィッティング
from iminuit import Minuit # CERN製の最小化ライブラリ
from iminuit.util import describe # 関数引数名の抽出に使う
import pandas as pd # データフレーム操作用ライブラリ
# --- グローバル定数の定義 ---
XMIN = 5870 # x軸の最小値(例えばスペクトルの波長やエネルギー)
XMAX = 5920 # x軸の最大値
BINSIZE = 200 # データ点の数(binの数)
X = np.linspace(XMIN, XMAX, BINSIZE) # 等間隔のx値を生成
# --- フィッティングモデルの定義 ---
def model(x, p):
# モデルは2つのガウス分布+直線的なバックグラウンド(傾きあり)
amp1, amp2, mu1, mu2, sigma, bkg0, bkg1 = p
return (
amp1 * np.exp(-0.5 * ((x - mu1) / sigma) ** 2) + # ガウス1
amp2 * np.exp(-0.5 * ((x - mu2) / sigma) ** 2) + # ガウス2
bkg0 + bkg1 * (x - XMIN) # バックグラウンド(一次関数)
)
# --- 合成データの生成 ---
def generate_data(seed=42):
# 真のパラメータ(観測データを模擬する)
amp1_true, amp2_true = 10, 20
mu1, mu2 = 5890, 5900
sigma = 2.0
bkg0_true, bkg1_true = 10, -0.1
# モデルによる真のy値を生成
y_true = model(X, [amp1_true, amp2_true, mu1, mu2, sigma, bkg0_true, bkg1_true])
# ノイズとしてポアソン乱数を加えて「観測データ」を作る
np.random.seed(seed)
y_obs = np.random.poisson(y_true)
# 誤差は √N(ポアソン統計を仮定)
y_err = np.sqrt(np.maximum(y_obs, 1)) # 0除算を防ぐため max(1, y)
return y_obs, y_err, y_true
# --- Scipy による最小二乗フィッティング ---
def fit_least_squares(x, y, yerr, init_p, use_pinv=True):
def residuals(p):
return (y - model(x, p)) / yerr # 標準化残差(誤差で割る)
result = least_squares(residuals, init_p) # 最小化実行
# 共分散行列の計算(逆行列 or 擬似逆行列)
J = result.jac # ヤコビ行列(勾配)
res = result.fun # フィット後の残差
sigma2 = np.sum(res**2) / (len(y) - len(init_p)) # 誤差スケール
cov = np.linalg.pinv(J.T @ J) * sigma2 if use_pinv else np.linalg.inv(J.T @ J) * sigma2
return result.x, np.sqrt(np.diag(cov)) # 最適化パラメータとその誤差
# --- Minuit を用いたフィッティング ---
def fit_minuit(x, y, yerr, init_p, use_minos=False):
# 最小化関数(カイ二乗)
def chi2(amp1, amp2, mu1, mu2, sigma, bkg0, bkg1):
p = [amp1, amp2, mu1, mu2, sigma, bkg0, bkg1]
return np.sum(((y - model(x, p)) / yerr) ** 2)
names = describe(chi2) # パラメータ名の取得
init_dict = dict(zip(names, init_p)) # 初期値を辞書化
m = Minuit(chi2, **init_dict)
m.errordef = Minuit.LEAST_SQUARES # 最小二乗法の誤差定義
m.migrad() # 最小化
m.hesse() # 共分散行列による誤差評価
if use_minos:
# MINOSによる非対称誤差の評価(計算コスト高)
m.minos()
err = []
for name in names:
me = m.merrors.get(name)
if me is not None and me.is_valid:
err.append(max(abs(me.lower), abs(me.upper))) # 上下誤差の大きい方を採用
else:
err.append(np.nan)
else:
err = [m.errors[name] for name in names]
return np.array([m.values[name] for name in names]), np.array(err)
# --- 結果の保存と可視化関数 ---
def save_fit_result_csv(param_names, fit_name, values, errors, prefix='fitresult'):
# フィット結果を CSV に保存
df = pd.DataFrame({
'Parameter': param_names,
f'{fit_name}_fit': values,
f'{fit_name}_err': errors
})
fname = f"{prefix}_{fit_name}.csv"
df.to_csv(fname, index=False)
print(f"Saved {fname}\n")
print(df.to_string(index=False, float_format="%.4f"))
return fname
def save_data_and_model(x, y, yerr, yfit, label, prefix='datamodel'):
# 元データとフィット曲線をCSVに保存
df = pd.DataFrame({
'x': x,
'y_obs': y,
'y_err': yerr,
f'{label}_fit': yfit
})
fname = f"{prefix}_{label}.csv"
df.to_csv(fname, index=False)
print(f"Saved {fname}")
return fname
def plot_comparison(datafiles, title="Fit Comparison", offset=False, offset_val=10):
# 複数のフィット結果を並べて描画(視認性のためにオフセット可)
plt.figure(figsize=(10, 6))
for i, fname in enumerate(datafiles):
label = fname.split('_')[-1].replace(".csv", "")
df = pd.read_csv(fname)
y_offset = i * offset_val if offset else 0
model_label = f'{label} fit' + (f" (offset={y_offset})" if offset else "")
plt.errorbar(df['x'], df['y_obs'] + y_offset, yerr=df['y_err'], fmt='o', ms=3, alpha=0.3,
label='Observed')
plt.plot(df['x'], df.filter(like='_fit').values[:, 0] + y_offset , "--", alpha=0.8, label=model_label)
plt.legend()
plt.xlabel("Energy (eV)")
plt.ylabel("Counts (+offset)")
plt.title(title)
plt.grid(True, alpha=0.2)
plt.tight_layout()
plt.savefig("fit_comparison_all.png")
plt.show()
def save_fit_result_csv_asymmetric(param_names, fit_name, values, errors_lower, errors_upper, prefix='fitresult'):
# 非対称誤差を含むフィット結果をCSV保存
df = pd.DataFrame({
'Parameter': param_names,
f'{fit_name}_fit': values,
f'{fit_name}_err_lower': errors_lower,
f'{fit_name}_err_upper': errors_upper
})
fname = f"{prefix}_{fit_name}.csv"
df.to_csv(fname, index=False)
print(f"Saved {fname}\n")
print(df.to_string(index=False, float_format="%.4f"))
return fname
# --- MINOSを使って非対称誤差を取得 ---
def fit_minuit_with_minos_asymmetric(x, y, yerr, init_p):
"""iminuit でフィットし、非対称誤差(lower, upper)も取得する"""
def chi2(amp1, amp2, mu1, mu2, sigma, bkg0, bkg1):
p = [amp1, amp2, mu1, mu2, sigma, bkg0, bkg1]
return np.sum(((y - model(x, p)) / yerr) ** 2)
names = describe(chi2)
init_dict = dict(zip(names, init_p))
m = Minuit(chi2, **init_dict)
m.errordef = Minuit.LEAST_SQUARES
m.migrad()
m.hesse()
m.minos() # 非対称誤差を得るために必要
values = [m.values[name] for name in names]
errors_lower = []
errors_upper = []
for name in names:
me = m.merrors.get(name)
if me is not None and me.is_valid:
errors_lower.append(me.lower)
errors_upper.append(me.upper)
else:
errors_lower.append(np.nan)
errors_upper.append(np.nan)
return names, np.array(values), np.array(errors_lower), np.array(errors_upper)
# --- 実行メイン関数 ---
def main():
# 擬似データ生成
y_obs, y_err, y_true = generate_data()
# フィット初期値の設定
init_p = [9, 18, 5890, 5900, 2.0, 5, 0.0]
param_names = ['amp1', 'amp2', 'mu1', 'mu2', 'sigma', 'bkg0', 'bkg1']
results = []
# Scipy + 擬似逆行列でフィット
vals, errs = fit_least_squares(X, y_obs, y_err, init_p, use_pinv=True)
csv1 = save_fit_result_csv(param_names, "scipy_pinv", vals, errs)
csv2 = save_data_and_model(X, y_obs, y_err, model(X, vals), "scipy_pinv")
results.append(csv2)
# Scipy + 通常の逆行列でフィット
vals, errs = fit_least_squares(X, y_obs, y_err, init_p, use_pinv=False)
csv1 = save_fit_result_csv(param_names, "scipy_inv", vals, errs)
csv2 = save_data_and_model(X, y_obs, y_err, model(X, vals), "scipy_inv")
results.append(csv2)
# Minuit(MINOSあり)でフィット(誤差は最大幅)
vals, errs = fit_minuit(X, y_obs, y_err, init_p, use_minos=True)
csv1 = save_fit_result_csv(param_names, "minuit_minos", vals, errs)
csv2 = save_data_and_model(X, y_obs, y_err, model(X, vals), "minuit_minos")
results.append(csv2)
# Minuit + 非対称誤差取得
param_names, vals, errs_lower, errs_upper = fit_minuit_with_minos_asymmetric(X, y_obs, y_err, init_p)
csv1 = save_fit_result_csv_asymmetric(param_names, "minuit_asym", vals, errs_lower, errs_upper)
csv2 = save_data_and_model(X, y_obs, y_err, model(X, vals), "minuit_asym")
results.append(csv2)
# 結果をオフセット表示で比較
plot_comparison(results, offset=True)
# 実行
main()
実行結果
Saved fitresult_scipy_pinv.csv
Parameter scipy_pinv_fit scipy_pinv_err
amp1 9.1072 1.1686
amp2 19.3929 1.5649
mu1 5890.1225 0.3006
mu2 5899.7758 0.1593
sigma 1.9618 0.1277
bkg0 8.9090 0.4615
bkg1 -0.0985 0.0132
Saved datamodel_scipy_pinv.csv
Saved fitresult_scipy_inv.csv
Parameter scipy_inv_fit scipy_inv_err
amp1 9.1072 1.1686
amp2 19.3929 1.5649
mu1 5890.1225 0.3006
mu2 5899.7758 0.1593
sigma 1.9618 0.1277
bkg0 8.9090 0.4615
bkg1 -0.0985 0.0132
Saved datamodel_scipy_inv.csv
Saved fitresult_minuit_minos.csv
Parameter minuit_minos_fit minuit_minos_err
amp1 9.1052 1.0973
amp2 19.3846 1.5085
mu1 5890.1224 0.3034
mu2 5899.7759 0.1481
sigma 1.9623 0.1230
bkg0 8.9090 0.4328
bkg1 -0.0985 0.0124
Saved datamodel_minuit_minos.csv
Saved fitresult_minuit_asym.csv
Parameter minuit_asym_fit minuit_asym_err_lower minuit_asym_err_upper
amp1 9.1052 -1.0814 1.0973
amp2 19.3846 -1.4601 1.5085
mu1 5890.1224 -0.2938 0.3034
mu2 5899.7759 -0.1477 0.1481
sigma 1.9623 -0.1200 0.1230
bkg0 8.9090 -0.4328 0.4320
bkg1 -0.0985 -0.0124 0.0124
Saved datamodel_minuit_asym.csv
実行結果です。offset は、あくまで見た目の上でデータが重ならないように縦方向に少しずらして表示しただけです。
下記の4種類のパターンで違いを評価できるような例にしております。
- Scipy + 擬似逆行列でフィット
- Scipy + 通常の逆行列でフィット
- Minuit(MINOSあり)でフィット(誤差は最大幅)
- Minuit + 非対称誤差取得
まとめ
| 特徴 | Scipy | iminuit (MINOSあり) |
|---|---|---|
| 実装の手軽さ | ◎ 簡単 | ○ 少し複雑 |
| 誤差推定の正確性 | △ 対称のみ | ◎ 非対称も対応可能 |
| 科学研究向き | △ | ◎ CERN由来、信頼性高 |
おわりに
今回の記事では、スペクトルデータのフィッティングに必要な基本的知識を、Scipyとiminuitを使って段階的に解説しました。研究や実験データ処理において、「どのくらいの信頼性で値が求まっているか?」を定量的に知ることはとても重要です。
Voigt関数などより現実的なモデルへの対応も可能です。