python で直線フィットとガウシアンフィットをする簡単な方法

Last updated at 2024-06-26Posted at 2019-01-11

python で fitting する簡単な例

概要

python でモデルフィットしてエラーを出すための簡単な方法を示す。極力短いコードで確実に動くサンプルを意図したので、エラー判定や細かな処理はしておりません。コードを見ればOKな人は私のgoogle Colab のページを参照ください。

フィットとは？

その前に、フィットとはどういう手続かを確認しておく。

データとモデルと用意する。ここでのモデルは、変数と定数を与えると値を返す関数である。
モデルの定数を与え、変数の初期値をセットする。
データとモデルの合具合を評価する関数を定義する。原理的には何でもよいが、カイ２乗値を使うことが多いので、この例ではそれに準じる。要するに、モデルとデータのズレの量である。初期値から計算を始め、ズレが最小になるように変数を初期値から動かし、ズレが極小になる場所を見つける(e.g, Levenberg-Marquardt Method)。ここではscipyの実装されたLM法 scipy.optimize.leastsq を用いる。(より一般的な場合は最後に補足)
個々のパラメータに付随する誤差および"モデルとの合い具合"を評価する。LM法では、エラーは変数の誤差の共分散行列の対角成分を信頼区間として評価するのでこれに準じた。注意としては、この方法では誤差は必ず正負で同じになり、科学論文で使えるエラーかどうかは考える必要ある。(e.g., X線衛星業界の話だと，xspec では error コマンドを使ってエラーを求めなさい、と同じ。)

これに準じてソースコードを書いた。

コードをみたらOKな人はこれを読んでください。

サンプルコード

直線フィットとガウシアンフィットの例を示す。

どちらもデータをベタにコードに書いて、初期値は適当にセットした。モデルの初期値は重要で、これが全然違うと収束しないことには注意する。この例ではそこそこな値を手打ちしてある。
モデルは mymodel という関数で設定する。下記の例では定数 consts は使ってないが、必要ならこれで定数を設定できる。パラメータの数や定数の数も任意に変更できるが、計算途中で発散が zero div が発生しないようには注意が必要。
mymodel関数の引数は xvalues,yvalues,params,constsの４つ用意しているが、yvaluesはこの例では使っていない。yの値にモデルが依存する場合に使う。
so.leastsq はカイ二乗値を計算するcalcchi関数、モデルの初期値param_init,calcchi関数の初期値以外のパラメータargs=(consts,model_func, xvalues, yvalues, yerrors)で必要である。またこの例は,yerrorsにゼロが含まれるときにzero div が発生してコケる。エラーがゼロにならないように使うこと。カウント数がゼロになるような場合はそもそもカイ二乗の最小化をすることが正しくない(詳細は後述を参考)。
エラーは誤差行列から出したエラーなので、科学的に〇〇%の信頼区間などを厳密に議論したい場合はこのエラーでよいかは検討が必要。中心値はLM法で求めたものがよく合っているなら、他の手法でも大して変わらないことが多い。

python での直線フィットの例

fit_linear.py

fit_linear.py


#!/usr/bin/env python

__version__= '1.0'
# This is created from the code made by M.Sawada during SXS tests. 

import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'serif'
import numpy as np
import scipy as sp
import scipy.optimize as so

def calcchi(params,consts,model_func,xvalues,yvalues,yerrors):
    model = model_func(xvalues,yvalues,params,consts)
    chi = (yvalues - model) / yerrors
    return(chi)

# optimizer
def solve_leastsq(xvalues,yvalues,yerrors,param_init,consts,model_func):

    param_output = so.leastsq(
        calcchi,
        param_init,
        args=(consts,model_func, xvalues, yvalues, yerrors),
        full_output=True)
    param_result, covar_output, info, mesg, ier = param_output
    error_result = np.sqrt(covar_output.diagonal())
    dof = len(xvalues) - 1 - len(param_init)
    chi2 = np.sum(np.power(calcchi(param_result,consts,model_func,xvalues,yvalues,yerrors),2.0))
    return([param_result, error_result, chi2, dof])

# model
def mymodel(xvalues,yvalues,params,consts): 
    p0,p1 = params
    c0,c1 = consts
    model_y = p0*xvalues + p1
#    model_y = p0*np.exp(-0.5*((xvalues-p1)/p2)**2.) + c1
#    model_y = p0*np.exp(-0.5*((xvalues-p1)/p2)**2.) + c0*xvalues + c1
    return(model_y)
            
# set data
x  = np.array([ 1, 2, 3,  4,  5, 6, 7,  8,  9, 10, 11, 12, 13, 14, 15])
y  = np.array([ 1, 2, 5,  4,  8, 5, 9, 10, 13, 11, 15,  9, 10, 17, 25])
ye = np.array([ 3, 3, 2,  2,  3, 2, 3,  5,  6, 1,  3,  1,  3,  3,  2])

# initialize parameter 
a_init = 1.
b_init = 0.5
init_params = np.array([a_init, b_init])
# initialize constants 
consts = np.array([0,0]) 

# do fit 
result, error, chi2, dof = solve_leastsq( x, y, ye, init_params, consts, mymodel)

# get results 
a = result[0]
b = result[1]
ae = error[0]
be = error[1]

label = "Y = " + str("%4.2f(+/-%4.2f) " % (a,ae) ) + " X + " + str("%4.2f(+/-%4.2f)" % (b,be) )
print(label)

# plot results
plt.title("Linear fit : " + label)
model_y = mymodel(x,y,result,consts)
plt.errorbar(x, y, yerr = ye, fmt="bo")
plt.plot(x, model_y, 'r-')

plt.savefig("linearfit.png")
plt.show()

結果の絵がこちら。

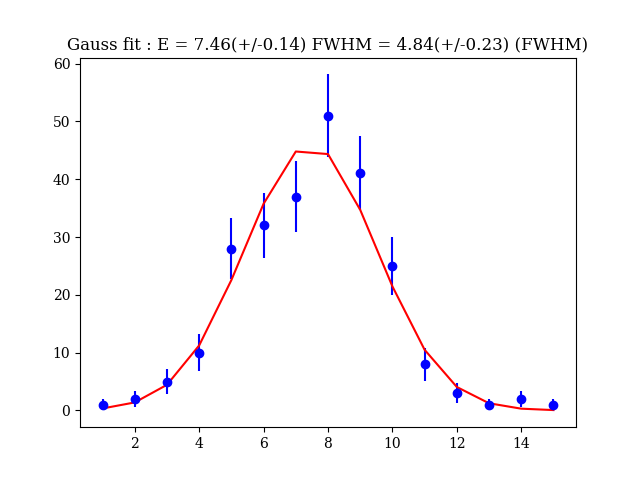
python を用いたガウシアンフィットの例

fit_gauss.py

fit_gauss.py


#!/usr/bin/env python

__version__= '1.0'
# This is created from the code made by M.Sawada during SXS tests. 

import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'serif'
import numpy as np
import scipy as sp
import scipy.optimize as so

def calcchi(params,consts,model_func,xvalues,yvalues,yerrors):
    model = model_func(xvalues,yvalues,params,consts)
    chi = (yvalues - model) / yerrors
    return(chi)

# optimizer
def solve_leastsq(xvalues,yvalues,yerrors,param_init,consts,model_func):

    param_output = so.leastsq(
        calcchi,
        param_init,
        args=(consts,model_func, xvalues, yvalues, yerrors),
        full_output=True)
    param_result, covar_output, info, mesg, ier = param_output
    error_result = np.sqrt(covar_output.diagonal())
    dof = len(xvalues) - 1 - len(param_init)
    chi2 = np.sum(np.power(calcchi(param_result,consts,model_func,xvalues,yvalues,yerrors),2.0))
    return([param_result, error_result, chi2, dof])

# model
def mymodel(xvalues,yvalues,params,consts): 
    p0,p1,p2 = params
    c0,c1 = consts
#    model_y = p0*xvalues + p1 
    model_y = p0*np.exp(-0.5*((xvalues-p1)/p2)**2.) + c1
#    model_y = p0*np.exp(-0.5*((xvalues-p1)/p2)**2.) + c0*xvalues + c1
    return(model_y)

# set data
x = np.array([ 1, 2, 3,  4,  5, 6,   7,  8,  9, 10, 11, 12, 13, 14, 15])
y = np.array([ 1, 2, 5, 10, 28, 32, 37, 51, 41, 25,  8,  3,  1,  2,  1])

# initialize parameter 
sigma_init = 5.
norm_init = 10.
init_params = np.array([norm_init, np.mean(x), sigma_init ])
# initialize constants 
consts = np.array([0,0]) 

# do fit 
result, error, chi2, dof = solve_leastsq( x, y, np.sqrt(y), init_params, consts, mymodel)

# get results 
ene = result[1]
sigma = np.abs(result[2])

enee = error[1]
sigmae = np.abs(error[2])

fwhm = 2.35 * sigma
fwhme = 2.35 * sigmae

label = "E = " + str("%4.2f(+/-%4.2f)" % (ene,enee)) + " FWHM = " + str("%4.2f(+/-%4.2f)" % (fwhm,fwhme) + " (FWHM)")
print(label)

# plot results
plt.title("Gauss fit : " + label)
model_y = mymodel(x,y,result,consts)
plt.errorbar(x, y, yerr = np.sqrt(y), fmt="bo")
plt.plot(x, model_y, 'r-')

plt.savefig("gaussfit.png")
plt.show()

結果の絵がこちら。あるいは、google Colab のページを参照ください。

モデルがガタガタしてみえるのは、簡単のため、データ点と同じ数だけモデルも描画しているため。例えば、numpy.interp などでデータ点数を増やしてモデルを表示すると綺麗になる。使い方は，y = np.interp(サンプリングしたいX座標の配列, 既知のX座標の配列, 既知のY座標の配列) のように，既知のx, y のペアを入れて，知りたい x 座標を入れると，知りたい y の値がかえってくる．これは単なる台形補完による内層なので，予想された範囲内の補完値しかでてこないので実験等では重宝します．

エラーについての補足

誤差は、numpy.diagonal で誤差の分散共分散行列の対角成分のルートをとってつけている。これは、エラーがガウス分布すると仮定すると、カイ２乗分布するパラメータの Hessian 行列の逆行列が、パラメータが真値(極小値)に近い時に、パラメータの誤差の分散共分散行列に一致するためである。

http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/DAVIES1/rd_bhatt_cvonline/node9.html
https://www.psychologie.uni-heidelberg.de/ae/meth/team/mertens/blog/hessian.nb.html
Hessian and Covariance Matrix 「Hessian matrix is equal to the inverse of the covariance matrix」 Hessian 行列の対角成分は、誤差行列(ガウシアンのシグマの２乗が対角に詰まった)の逆数になるので、Hessian 行列の逆行列のルートをとると標準偏差(~=パラメータの誤差)が得られる。

Hessian の逆行列(= sigma^2) 生成 ==> covariant Matrix を生成 ==> covariant Matrix の対角成分が誤差行列となる。 ２つの異なるパラメータの誤差や相関などは一切考慮してないことに注意

別の言い方としては、Fisher 情報量と Cramér–Rao (クラメール-ラオ)の不等式とか考えると、

何か下限値があって、それは確率分布関数の極値近傍の曲率に相当するような量(の逆数）が適切なような気がするので、+/-で対照的な誤差をつけるということは、曲率でえいやっと誤差をつけたことに相当するのだと思ってます。

より一般的な場合についての補足

この例は最も簡単なフィットのケースである。例えば、ポアソン統計が必要な場合は、ガウス分布ではなくてポアソン分布を使う必要があるので、カイ２乗の最小化問題ではなくなる。これにより、より一般的な非線形関数の最小化問題になる(カイ２乗の場合は二乗する関数の最小化という事前情報を使えたため高速で計算できた)。興味のある方は、下記のいつくかの文献を参考にしてほしい。

xspec の C 統計 : https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/XSappendixStatistics.html　
ガウス統計とポアソン統計の比較の例 : https://academic.oup.com/pasj/article-abstract/71/4/75/5536242
計算方法 : https://link.springer.com/article/10.1007/s10909-014-1098-4

そのほか、微分不可能な関数の最小化が必要な場合は、

など参考にしてください。

制限付きフィット、または voigt 関数のフィットの例

scipy.optimize と lmfit の非線形最小二乗フィットの比較

背景の補足

lmfit と scipy.optimize の両方が非線形最小二乗フィットのためのツールを提供していますが、それぞれの機能と使いやすさには違いがあります。これら二つのライブラリを比較し、自分のニーズに合ったツールを選ぶと良いです。

scipy.optimize.leastsq

scipy.optimize.leastsq は、Levenberg-Marquardt アルゴリズムを使用した非線形最小二乗フィットの基本的な実装です。これは SciPy ライブラリの一部です。

特徴

軽量: 最小限のオーバーヘッドで基本的な機能を提供。
柔軟性: 広範なカスタマイズと制御が可能。
汎用性: 様々な最適化問題に適用可能。

使用例

import numpy as np
from scipy.optimize import leastsq

# モデル関数の定義
def model(params, x):
    return params[0] * x + params[1]

# 残差関数の定義
def residuals(params, x, y):
    return y - model(params, x)

# データ
x = np.array([1, 2, 3, 4, 5])
y = np.array([1.1, 2.0, 3.0, 4.1, 5.1])

# パラメータの初期値
params_initial = [1, 0]

# フィットの実行
params_fit, _ = leastsq(residuals, params_initial, args=(x, y))

print("フィットされたパラメータ:", params_fit)
# フィットされたパラメータ: [1.01 0.03]

lmfit

lmfit は、非線形最小二乗フィットのために設計された高レベルのライブラリで、scipy.optimize の上に構築されています。使いやすいインターフェースと追加機能を提供します。

特徴

高レベルインターフェース: ユーザーフレンドリーなAPIでフィットプロセスを簡素化。
包括的な出力: パラメータの不確実性や相関を含む詳細なフィットレポートを提供。
制約と境界: パラメータの制約と境界の設定が容易。
組み込みモデル: 一般的なフィットタスクのための多くの事前定義モデルを提供。

使用例

import numpy as np
from lmfit import Model

# モデル関数の定義
def model_func(x, a, b):
    return a * x + b

# モデルの作成
model = Model(model_func)

# データ
x = np.array([1, 2, 3, 4, 5])
y = np.array([1.1, 2.0, 3.0, 4.1, 5.1])

# 初期パラメータ
params = model.make_params(a=1, b=0)

# フィットの実行
result = model.fit(y, params, x=x)

# フィットレポートの表示
print(result.fit_report())

実行結果は、

[[Model]]
    Model(model_func)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 5
    # variables        = 2
    chi-square         = 0.01100000
    reduced chi-square = 0.00366667
    Akaike info crit   = -26.5964896
    Bayesian info crit = -27.3776138
    R-squared          = 0.99892284
[[Variables]]
    a:  1.01000000 +/- 0.01914852 (1.90%) (init = 1)
    b:  0.03000000 +/- 0.06350850 (211.69%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(a, b) = -0.905

となります。

比較

特徴	`scipy.optimize.leastsq`	`lmfit`
インターフェース	低レベル	高レベル
使いやすさ	設定とカスタマイズが必要	ユーザーフレンドリー、最小限の設定
出力	基本的なパラメータ	詳細なフィットレポート
パラメータ制約	手動での実装	組み込みサポート
組み込みモデル	なし	あり
適したユーザー	柔軟性を必要とする経験豊富なユーザー	使いやすさと詳細な解析を必要とするユーザー

まとめ

scipy.optimize.leastsq と lmfit はどちらも非線形最小二乗フィットのための強力なツールで、それぞれ異なる強みがあります。scipy.optimize.leastsq は柔軟性と制御を提供し、経験豊富なユーザーに適しています。一方、lmfit は使いやすいインターフェースと追加機能を提供し、詳細なフィットレポートやパラメータ制約を必要とするユーザーに適しています。どちらを選ぶかは、ユーザーの具体的なニーズと経験レベルに依存します。サイエンス用途では、一般に評価関数をカスタマイズ(ポアソン分布のlikelihoodを使いたいとか)したい場合や、非対称の誤差までしっかり出したい、あるいは、非対称な誤差のコントアを描きたいなど、誤差の計算を丁寧に評価したい場合があるので、結局そういう場合は、どちらであっても深く理解して使う必要が出てきます。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up