フォークト関数 (Voigt function)とは?
フォークト関数 (Voigt function) は、ガウス分布とローレンツ分布の畳み込みした関数のことである。英語版のwikipediaには詳細な記載はあるが、日本語版にはない。
蛍光X線の自然幅が無視できないような精密分光をする場合などは避けては通れない関数である。畳み込みを計算するよりは、Faddeeva function を使うほうが早い。ここではpythonで簡単にVoigt関数を書く方法を紹介したい。一応,定義を書き下しておく.
V(x;\sigma,\gamma) \equiv \int_{-\infty}^{\infty} G(x';\sigma) L(x-x';\gamma)dx' = \frac{Re[w(z)]}{\sigma \sqrt{2\pi}}
とかける,ここで,Voigt関数は$V(x;\sigma,\gamma)$ であり,
ガウス関数は G(x;σ)と,ローレンツ関数 L(x;γ)の畳み込みとして定義される.
$Re[w(z)]$ は Faddeeva 関数の実部で,$z = (x + i \gamma)/ σ\sqrt{2}$ の意味である.
python で voigt function のプロットのサンプル
scipy.special.wofz が Faddeeva function を返してくれるので、これを用いればOK。
# !/usr/bin/env python
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'serif'
import numpy as np
import scipy as sp
import scipy.special
def voigt(xval,params):
norm,center,lw,gw = params
# norm : normalization
# center : center of Lorentzian line
# lw : HWFM of Lorentzian
# gw : sigma of the gaussian
z = (xval - center + 1j*lw)/(gw * np.sqrt(2.0))
w = scipy.special.wofz(z)
model_y = norm * (w.real)/(gw * np.sqrt(2.0*np.pi))
return model_y
# plot init function
plt.title("Voigt function")
x = np.arange(0,100,0.1)
y0 = voigt(x,[1,np.mean(x),1,1])
plt.plot(x, y0/np.amax(y0), 'k-', label = "lw = 1, gw = 1")
y1 = voigt(x,[1,np.mean(x),1,10])
plt.plot(x, y1/np.amax(y1), '-', label = "lw = 1, gw = 10")
y2 = voigt(x,[1,np.mean(x),10,1])
plt.plot(x, y2/np.amax(y2), '-', label = "lw = 10, gw = 1")
y3 = voigt(x,[1,np.mean(x),10,10])
plt.plot(x, y3/np.amax(y3), '-', label = "lw = 10, gw = 10")
plt.legend(numpoints=1, frameon=False, loc="best")
plt.grid(linestyle='dotted',alpha=0.5)
plt.savefig("voigt.png")
plt.show()
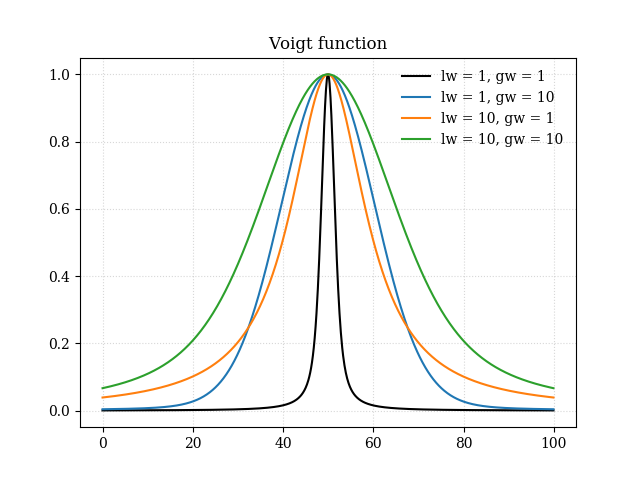
生成される図はこちら。ピークは同じ高さになるように規格化してある。lw が Lorentzianの幅で、gwがGaussianの幅である。Lerentzianの方が裾が幅広なので、lw が効くと裾の大きい形状になる。
分光においては、Lorentzianの裾を定量的に知りたいときがあるので、
半値幅の整数倍で見るガウシアンとローレンチアンの違い の記事も書いたので気になった方は参考ください。
Voigt 関数を用いたフィットの例
pythonでパラメータの制限付きでfittingを行う方法 を参考。
その他のライブラリ
ROOTには、TMathクラスに TMath:Voigt が定義されている。上記と同様にFaddeeva関数を用いた実装である。