scikit-learn サポートベクタマシン

サポートベクタマシンとは

サポートベクトマシン(Support Vector Machine, SVM)とは、教師あり学習のひとつで、分類をするためのアルゴリズムである。

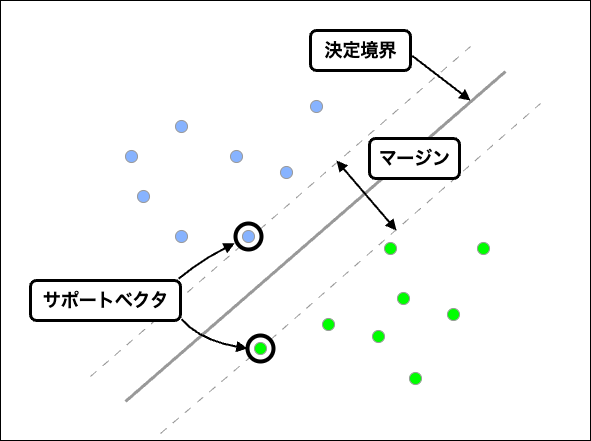
サポートベクタマシンを理解するために次の3つの概念を理解する。

• 決定境界 : データを分割する直線
• サポートベクタ : 決定境界に一番近い各クラスのデータの
• マージン : クラス間のサポートベクタの距離

サポートベクタマシンはこのマージンを最大化するように決定境界を引くことでデータを分類する。サポートベクタマシンは、境界線が非線形になる場合でも、カーネル関数を使って高次元空間へ線形分離することで、高精度な分類をすることができるのが特徴である。

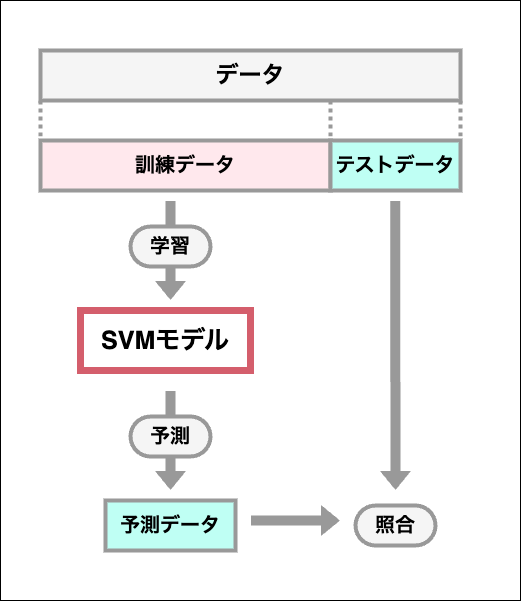
サポートベクタマシンの流れ

1. データの分割
   学習データ(訓練のためのデータ)とテストデータ(性能評価のためのデータ)に分割する
2. データの標準化
   各特徴量のスケールを合わせることで距離計算を正しく計算できる
3. モデルの作成・学習
   sklearn.svmモジュールのSVCクラスをモデルオブジェクトとして利用する
4. モデルの性能評価
   SVCクラスのscore()メソッドを利用して、モデルを使った結果と分割したテストデータを照合する

コード

以下はirisデータについて、がくの長さ(Sepal Length)とがくの幅(Sepal width)から2つの品種(Setosa,Versicolor)に分類するサポートベクタマシンのコードである。また、分類結果を決定境界とマージンを用いて可視化する。

ポイント

• irisデータの100件目までがSetosaとVersicolorについてのデータなので、100行目までのみ取り出して使っている
• サンプルの散布図のプロットと決定境界・マージンのプロットを行う関数plot_svm_decision_boundaryを定義し、訓練データとテストデータでそれぞれ関数を適用させている

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC


# 決定境界とマージンを可視化する関数
def plot_svm_decision_boundary(X,y,model,title,ax,is_train=False):
    '''
    Parameters
        X : 説明変数(2次元Numpy配列)
        y : 目的変数(1次元Numpy配列)
        model : svmモデル(SVC)
        ax : グラフ(Axes)
        is_train : テストの際はサポートベクタに印をつけないのでFalse
    '''

    # クラスごとに色分けされた散布図を作成
    ax.scatter(X[y==0, 0], X[y==0, 1], 
               c='blue', label='Setosa', edgecolors='k', s=100)
    ax.scatter(X[y==1, 0], X[y==1, 1], 
               c='green', label='Versicolor', edgecolors='k', s=100)

    # データの範囲を設定
    xmin = X[:,0].min() - 0.5
    xmax = X[:,0].max() + 0.5
    ymin = X[:,1].min() - 0.5
    ymax = X[:,1].max() + 0.5
    
    # グリッド線の作成
    xx, yy = np.meshgrid(np.linspace(xmin,xmax,100), np.linspace(ymin,ymax,100))
    xy = np.vstack((xx.ravel(),yy.ravel())).T

    # 決定境界とマージンの描画
    p = model.decision_function(xy).reshape(100,100)
    ax.contour(xx, yy, p,
               levels=[-1,0,1], alpha=0.5, colors="k",linestyles=["--","-","--"])
    
    # サポートベクトルの強調
    if is_train:
        ax.scatter(model.support_vectors_[:,0],
                   model.support_vectors_[:,1],
                   label="Support Vectors",
                   s=200, facecolors="none", edgecolors="orange")
    
    # グラフの装飾
    ax.set_title(title, fontsize=12, fontweight='bold')
    ax.set_xlabel("Sepal Length (standardized)", fontsize=11)
    ax.set_ylabel("Sepal Width (standardized)", fontsize=11)
    ax.legend()



# データの読み込み
iris = load_iris()

# データセットの用意
X = iris.data[:100,:2]
y = iris.target[:100]

# データセットの分割
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,shuffle=True,stratify=y)
print(f"X_train : {len(X_train)}件")
print(f"X_test : {len(X_test)}件")
print(f"y_train : {len(y_train)}件")
print(f"y_test: {len(y_test)}件")

# データの標準化
sc = StandardScaler()
X_train_sc = sc.fit_transform(X_train)
X_test_sc = sc.transform(X_test)

# モデルの作成と学習
model = SVC(kernel="linear",C=1.0)
model.fit(X_train_sc,y_train)

# 訓練データとテストデータの精度を評価
train_accuracy = model.score(X_train_sc,y_train)
test_accuracy = model.score(X_test_sc,y_test)
print(f"train_accuracy:{train_accuracy * 100:.1f}%")
print(f"test_accuracy:{test_accuracy * 100:.1f}%")

# 訓練データとテストデータの決定境界とマージンの可視化
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(15, 5))
plot_svm_decision_boundary(X_train_sc,y_train,model,"train",ax1,is_train=True)
plot_svm_decision_boundary(X_test_sc,y_test,model,"test",ax2)

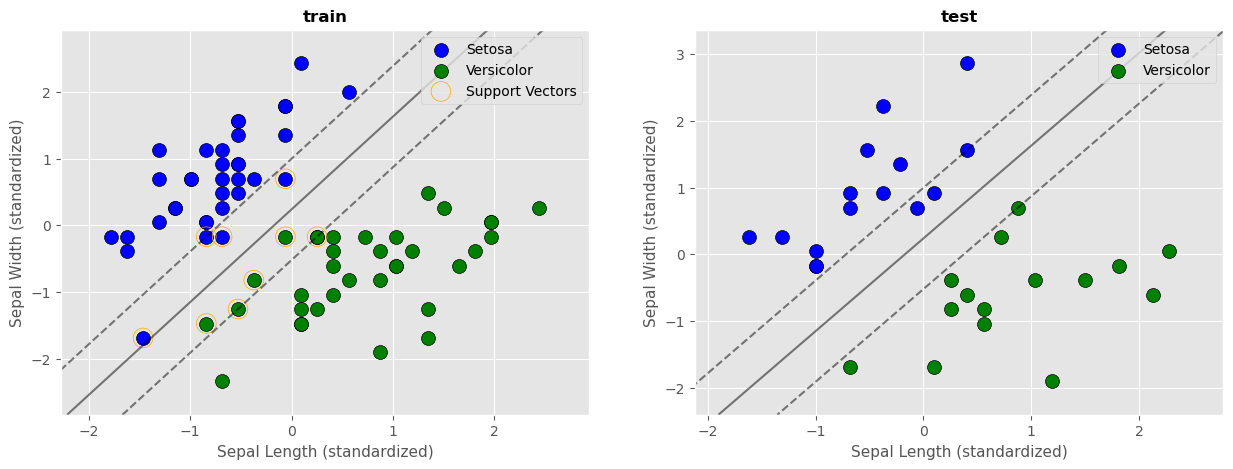
実行結果

X_train : 70件
X_test : 30件
y_train : 70件
y_test: 30件
train_accuracy:100.0%
test_accuracy:100.0%

1. 関数の定義

関数plot_svm_decision_boundaryは、説明データと目的データを受け取り、そのデータをクラスごと(目的変数ごと)に色分けして散布図を描画する。また、その散布図に決定境界とマージンをプロットする。

1-1クラスごとに色分けされた散布図を作成

2つの特徴量について、クラス0(Setosa)のサンプルを青、クラス1(Versicolor)のサンプルを緑で、散布図を描画する。

ax.scatter(X[y==0, 0], X[y==0, 1], 
           color='blue', label='Setosa', edgecolors='k', s=100)
ax.scatter(X[y==1, 0], X[y==1, 1], 
           color='green', label='Versicolor', edgecolors='k', s=100)

1-2データの範囲を設定

xmin = X[:,0].min() - 0.5
xmax = X[:,0].max() + 0.5
ymin = X[:,1].min() - 0.5
ymax = X[:,1].max() + 0.5

説明データの各列(第0列：Sepal Length、第1列：Sepal Width)の最大値、最小値より0.5だけ外側の値にする。

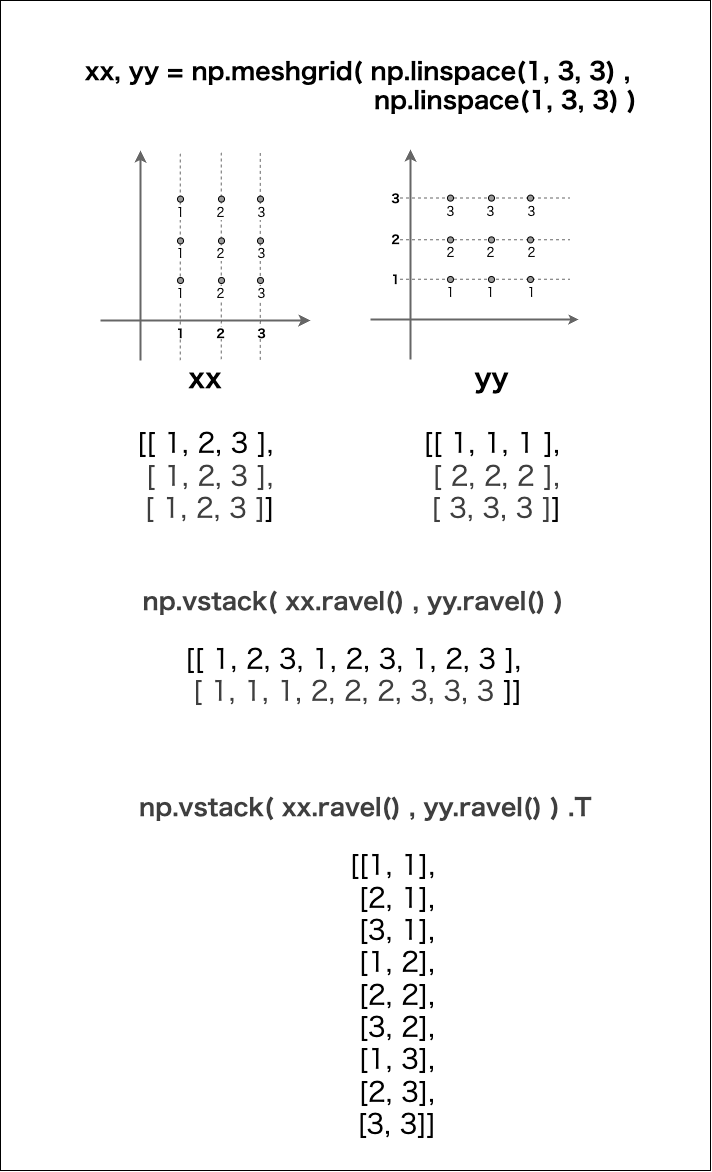
1-3グリッド線の作成

データの範囲内にグリッドを作成する。

xx, yy = np.meshgrid(np.linspace(xmin,xmax,100), np.linspace(ymin,ymax,100))
xy = np.vstack((xx.ravel(),yy.ravel())).T

①np.linspace()でx,y座標を等間隔に分割した要素数100の配列を作成し、それをnp.meshgrid()の引数に渡す。

np.meshgrid()の戻り値を、(第1変数,第2変数)に分割代入する。

• 第1変数 : x座標についての全ての座標を、y軸座標の数だけ並べた配列
• 第2変数 : y座標についての全ての座標を、x軸座標の数だけ並べた配列

② その2つの配列をいったん1次元にしてから縦に連結し、さらにその転置をとると、各座標を要素とする2次元配列を取得できる。

簡単な例で①と②の流れを確認する。

1-4決定境界とマージンの描画

SVCオブジェクトが持つdecision_function()メソッドは、各点がどのクラスに近いかを示す値を返す。

• 0 : 決定境界上にある
• 正 : クラス1に近い
• 負 : クラス0に近い

p = model.decision_function(xy).reshape(100,100)

ax.contour(X,Y,Z)は等高線をプロットする。

• X : x座標
• Y : y座標
• Z : xy座標での関数値(決定関数の値)
• levels=[-1,0,1] : 等高線を描くのは Zが-1,0,1の値のときにする
• colors="k" : 線の色を黒に指定する
• linestyles=["--","-","--"] : 線の種類を それぞれ点線,実線,点線に指定する

ax.contour(xx, yy, p,
           levels=[-1,0,1], alpha=0.5, colors="k",linestyles=["--","-","--"])

1-5サポートベクトルの強調

訓練データの時のみサポートベクトルに目印をつける。

if is_train:
    ax.scatter(model.support_vectors_[:,0],
               model.support_vectors_[:,1],
               label="Support Vectors",
               s=200, facecolors="none", edgecolors="orange")

　2. データの分割

データセットを訓練用データとテストデータに分けることで、未知のデータについての予測の精度を、既知のテストデータを使って測ることができるようになる。

データの分割にはsklearn.model_selectionモジュールのtrain_test_split(X,Y)関数を利用する。

• X : 説明変数データ
• Y : 目的変数データ
• test_size : テストデータに使用するデータの割合を小数点で指定する
• shuffle=True : データをシャッフルする
• stratify=y : 訓練データとテストデータの正解ラベルの割合を揃える

X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,shuffle=True,stratify=y)

3. データの標準化

sklearn.preprocessingモジュールのStandardScalerクラスを利用してデータを標準化する。データリークを防ぐため、テスト用データはfit()しない。

sc = StandardScaler()
X_train_sc = sc.fit_transform(X_train)
X_test_sc = sc.transform(X_test)

4.モデルの作成・学習

sklearn.svmモジュールのSVCクラスを利用する。オブジェクト生成時には、コンストラクタに以下の引数を指定する。

• kernel : カーネルを指定する "linear","rbf","poly"
• C : マージンの幅を設定する

学習の実行はfit()を使用する。

model = SVC(kernel="linear",C=1.0)
model.fit(X_train_sc,y_train)

5. モデルの性能評価

SVCクラスのscore()メソッドに説明データと目的データを渡してスコアの値を取得する。

train_accuracy = model.score(X_train_sc,y_train)
test_accuracy = model.score(X_test_sc,y_test)
print(f"train_accuracy:{train_accuracy * 100:.1f}%")
print(f"test_accuracy:{test_accuracy * 100:.1f}%")