はじめに
こちらの記事では以下の内容についてまとめています。
- 混同行列と4つの指標(適合率・再現率・F値・正解率)の概念とコード
- ROC曲線とAUCの概念とコード
分類モデルの評価
分類モデルの評価するための指標として、次の指標がある。
- 混同行列 : 分類精度を測る
- ROC曲線、AUC : 予測確率の正確さを測る
混同行列
混同行列とは、モデルの予測と結果の組み合わせを集計した表のこと。
- ( Positive, Negative ) = ( 正例と予測した, 負例と予測した )
- ( True, False ) = ( 予測が合っていた, 予測が間違っていた )
この組み合わせである2×2の行列になる。
| 実績が正例 | 実績が負例 | |
|---|---|---|
| 正例と予測 | tp True Positive 真陽性 |
fp False Positive 偽陽性 |
| 負例と予測 | fn False Negative 偽陰性 |
tn True Negative 真陰性 |
confusion_matrix()関数
混同行列はsklearn.metricsのconfusion_matrix関数で取得できる。
引数
- 第1引数 : 実績データ(numpy配列)
- 第2引数 : 予測データ(numpy配列)
-
labels: 表示するクラスラベルの順番を整数型のリストで指定する(デフォルトは昇順)
戻り値
行が実績,列が予測についての混同行列を2次元numpy配列にして返す。
また、正例(True) = 1,負例(False)=0とするので、以下のような構造になる。
| 予測 class 0 |
予測 class 1 |
|
|---|---|---|
| 実績 class 0 |
tn | fp |
| 実績 class 1 |
fn | tp |
irisデータセットを使って学習したSVMの分類モデルについての混同行列を表示する。
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
# データの取得
iris = load_iris()
X, y = iris.data[:100], iris.target[:100]
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=123)
# 学習実行
svc = SVC()
svc.fit(X_train, y_train)
# 予測結果
y_pred = svc.predict(X_test)
# 混同行列
labels = iris.target_names[:2]
cm = confusion_matrix(y_test, y_pred,labels=[0,1])
df = pd.DataFrame(cm,
index=["実績-" + label for label in labels],
columns=["予測-"+ label for label in labels])
print(df)
予測-setosa 予測-versicolor
実績-setosa 15 0
実績-versicolor 0 15
適合率、再現率、F値、正解率
混同行列から、分類の精度を表す4つの指標を導出することができる。
| 指標 | 内容 | 導出式 |
|---|---|---|
| 適合率 precision |
正例と予測したデータのうち、 実績が正例だったものの割合 |
$\frac{tp}{tp+fp}$ |
| 再現率 recall |
実績が正例だったデータのうち、 正例と予測したものの割合 |
$\frac{tp}{tp+fn}$ |
| F値 f1-score |
適合率と再現率の調和平均 | $2×\frac{1}{\frac{1}{適合率}+\frac{1}{再現率}}$ $=\frac{2×適合率×再現率}{適合率+再現率}$ |
| 正解率 accuracy |
全データのうち、 予測が合っているものの割合 |
$\frac{tp+tn}{tp+fp+fn+tn}$ |
適合率と再現率はトレードオフなので、その調和平均を取るF値は両者のバランスの良さを表す。
classification_report()関数
適合率、再現率、F値、正解率を知るには、sklearn.metricsモジュールのclassification_report関数を利用する。
引数
-
第1引数: 実績(numpy配列) -
第2引数: 予測(numpy配列)
戻り値
4つの指標の値について、表の形式をとった文字列で返す。
横方向 : 適合率(precision)、再現率(recall)、F値(f1-score)、データ件数(support)
縦方向 : 各クラス(0,1,2...)、正解率(accuracy)、マクロ平均(macro avg)、重み月平均(weighted avg)
先ほどのirisデータセットの適合率、再現率、F値、正解率を調べる。
from sklearn.metrics import classification_report
# 分類精度の各種指標
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 1.00 1.00 1.00 15
1 1.00 1.00 1.00 15
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30
交差検証
交差検証とは、データを複数に分割し、その一部を学習用、残りを評価用としてモデルの学習と評価を行うという処理を、データのグループを変えながら繰り返し行うことでモデルの汎化性能を評価する手法のこと。
cross_val_score()関数
交差検証を行うにはsklearn.model_selectionモジュールのcross_val_score 関数を利用する。交差検証はハイパーパラメータの最適化と合わせて使われることが多い。
引数
-
第1引数: モデルオブジェクト -
第2引数: 説明変数データ -
第3引数: 目的変数データ -
cv: 分割数(int) -
scoring: 評価に用いる指標("accuracy","r2","roc_auc"など( その他は公式ドキュメントを参照)
戻り値
交差検証を行い、scoringで指定した評価指標の値を要素とするnumpy配列を返す。cvで指定した分割数の数だけモデルの学習と評価を繰り返すので、この値がnumpy配列の要素数となる。
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
# データの取得
iris = load_iris()
X, y = iris.data[:100], iris.target[:100]
svc = SVC()
cross_val_score(svc, X, y, cv=10, scoring="precision")
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
ROC曲線・AUC
データの予測確率の正確さを表す指標としてROC曲線とAUCがある。
ROC曲線
各データが正例に属する確率を算出し、各データについて自身の確率以上のデータを全て正例と予測したと仮定した時の、真陽性率と偽陽性率をそれぞれ縦軸、横軸にプロットしたもの。
例として、以下のような25件のデータについて考える。
probカラムは正例である確率、actualカラムは実績を表し、probカラムについて高順に並んだデータである。
| data | prob | actual | |
|---|---|---|---|
| 0 | 1 | 0.98 | 1 |
| 1 | 2 | 0.95 | 1 |
| 2 | 3 | 0.90 | 0 |
| 3 | 4 | 0.87 | 1 |
| 4 | 5 | 0.85 | 0 |
| 5 | 6 | 0.80 | 0 |
| 6 | 7 | 0.75 | 1 |
| 7 | 8 | 0.71 | 1 |
| 8 | 9 | 0.63 | 1 |
| 9 | 10 | 0.55 | 0 |
| 10 | 11 | 0.51 | 0 |
| 11 | 12 | 0.47 | 1 |
| 12 | 13 | 0.43 | 0 |
| 13 | 14 | 0.38 | 0 |
| 14 | 15 | 0.35 | 0 |
| 15 | 16 | 0.31 | 1 |
| 16 | 17 | 0.28 | 1 |
| 17 | 18 | 0.24 | 0 |
| 18 | 19 | 0.22 | 0 |
| 19 | 20 | 0.19 | 1 |
| 20 | 21 | 0.15 | 0 |
| 21 | 22 | 0.12 | 0 |
| 22 | 23 | 0.08 | 1 |
| 23 | 24 | 0.04 | 0 |
| 24 | 25 | 0.01 | 0 |
この各データについて、自身の確率以上のデータを全て正例であるとみなしたときの真陽性率と偽陽性率を算出する。
真陽性率
全ての正例のうち、正例と予測して実績が正例であるものの割合
tpr=\frac{tp}{tp+fn}
偽陽性率
全ての負例のうち、正例と予測して実績が負例のものの割合
fpr = \frac{fp}{tn+fp}
例えば5件目のデータの時を考える。
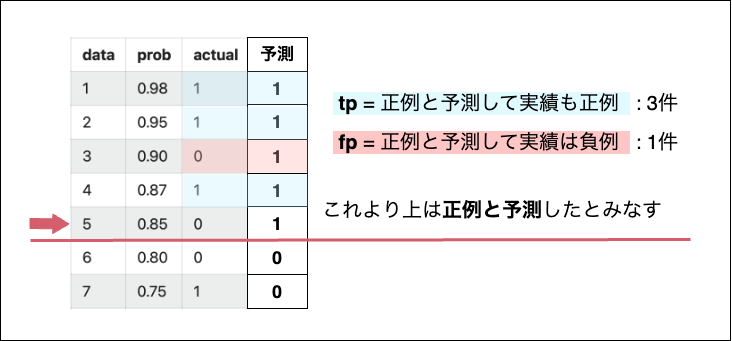
5件目を含めそれより上にあるデータは、全て正例で予測したとみなすという前提の上で、真陽性率と偽陽性率を算出する。
全ての正例は11件、正例と予測したうちで実績が正例のものは3件なので真陽性率は 3/11 となる。
全ての負例は14件、正例と予測したうちで実績が負例のものは1件なので偽陽性率は 1/14 となる。
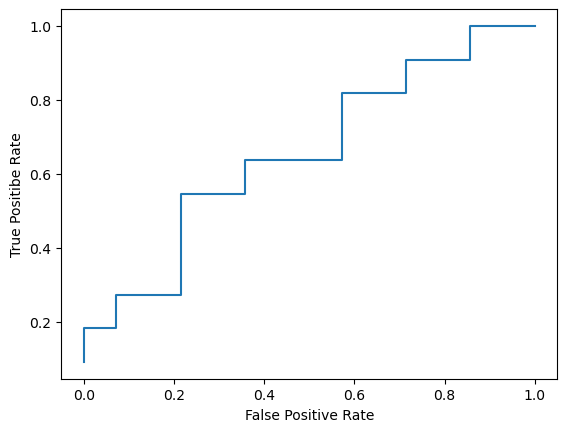
以上の処理を全てのデータについて行うと、25個の真陽性率と25個の偽陽性率のデータができるので、真陽性率のデータを縦軸、偽陽性率のデータを横軸にプロットした折れ線グラフがROC曲線である。
このROC曲線が左上に膨らんでいるほど、偽陽性率より真陽性率の方が高くなり、良いモデルであると評価できる。
AUC
ROC曲線の下側にできる図形の面積の値がAUC(Area Under the Curve)であり、モデルの良し悪しを図る指標になる。
AUCは、全てのデータについてFPRとTPRの積を出し、それを合計した値になる。
ROC曲線の形状とAUCの値の関係
| ROC曲線の形 | AUCの値 | モデルの評価 |
|---|---|---|
| 左上に膨らむ | 1に近い | 完璧な予想をしている |
| 対角線上に近づく | 0.5に近い | ランダムに予想している |
| 左下にしぼむ | 0に近い | 逆の予想をしている |
roc_curve関数
ROC曲線を描画するにはsklearn.metricsモジュールのroc_curve関数を利用する。
引数
-
第1引数: 実績の正例(numpy配列) -
第2引数: 正例となる確率(numpy配列)
正例となる確率は、モデルオブジェクトのpredict_proba()メソッドに、テスト用の説明変数データを渡して実行するとnumpy配列で取得できる。
戻り値
第1変数に偽陽性率、第2変数に真陽性率、第3変数に閾値が分割代入される。
(FPR, TPR, threshold) = roc_curve(y_test,t_prob)
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_curve, roc_auc_score
# データ取得
data = load_breast_cancer()
X, y = data.data, data.target
# データの分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
# モデルの作成と学習）
model = DecisionTreeClassifier(max_depth=3, random_state=42)
model.fit(X_train, y_train)
# 予測確率
y_prob = model.predict_proba(X_test)[:, 1]
# FPRとTPRの取得
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
auc = roc_auc_score(y_test, y_prob)
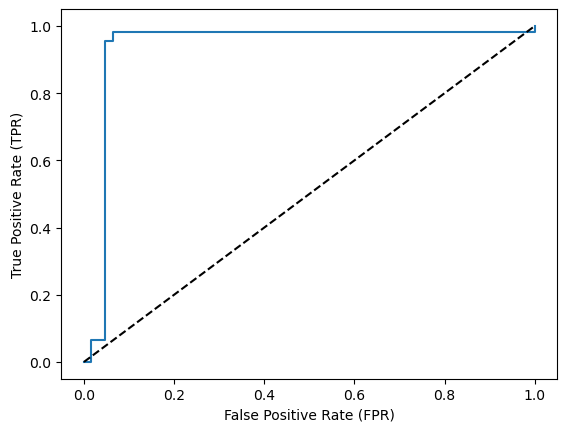
# ROC曲線の描画
fig, ax = plt.subplots()
ax.step(fpr, tpr, where='post', label=f'ROC curve (AUC={auc:.3f})')
ax.set_xlabel('False Positive Rate (FPR)')
ax.set_ylabel('True Positive Rate (TPR)')
ax.plot([0,1], [0,1], 'k--', label='Random')
plt.show()
