scikit-learn 決定木

はじめに

こちらの記事では、決定木について以下の内容をまとめました。

• 情報利得・ジニ不純度・エントロピーの式の意味についての直感的な理解
• scikit-learnにて、モデルの作成と学習・可視化を行う手順
• ランダムフォレストの実行手順

決定木とは

決定木とは、Yes/No形式の質問を繰り返してデータを分類・予測する機械学習手法のこと。データを木構造で表現し、各分岐点(ノード)で最も情報利得が大きくなるように分割を行う。

情報利得

親ノードから子ノードにデータを分割する際、どれだけ不純度を減らしているかを表す指標のこと。

情報利得 =(親ノードの不純度) - (子ノードの不純度の加重平均)

加重平均を取るというのは、グループの大きさを考慮に入れるということ。

子ノードの不純度の加重平均 = \sum_{i=1}^{C}\Bigg(\frac{グループiのデータ数}{親ノードのデータ数} × グループiの不純度\Bigg)

加重平均を取ることで、極端にデータ数が少なくて不純度の小さい(純粋な)グループによる影響を受けないようにすることができる。

不純度

不純度を求めるための指標には、次の3つがある。

1. ジニ不純度
2. エントロピー
3. 分類誤差

1. ジニ不純度

データを分割した時、ひとつのグループにどれだけのクラスが混在しているかを表す指標のこと。ジニ不純度が低いほどきれいに分割できていることになる。

クラスが$C$個あるとき、不純度$Gini$は以下のように求めることができる。

Gini = 1-\sum_{c=1}^{C}P(c)^2

$P(c)$は クラス$c$となる確率なので、$\frac{クラスcのデータ数}{分割前の全データ数}$でもあり、次のようにも書ける。

Gini =1-\sum_{i=1}^{C}(\frac{n_{i}}{N})^2\

ジニ不純度の取りうる値の範囲は、

0≦Gini≦1-\frac{1}{C}

となり、0に近いほど純度が高く良い分割と言える。

例えば以下のような分類をした場合の情報利得を求める。

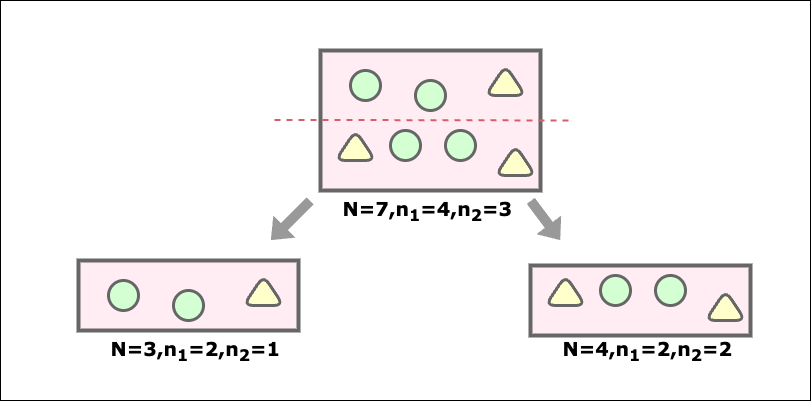
親ノードの不純度は

G(S)=1-\Bigg(\bigg(\frac{4}{7}\bigg)^2+\bigg(\frac{3}{7}\bigg)^2\Bigg)≒0.48

左子ノードの不純度は

1-\Bigg(\bigg(\frac{2}{3}\bigg)^2+\bigg(\frac{1}{3}\bigg)^2\Bigg)\approx 0.44

右子ノードの不純度は

1-\Bigg(\bigg(\frac{2}{4}\bigg)^2+\bigg(\frac{2}{4}\bigg)^2\Bigg)=0.5

子ノードの加重平均を求めるには、各グループの大きさを考慮するため、各子ノードの不純度に加重度をかける。

子ノードの加重平均 = \Bigg(\frac{3}{7}×0.44 + \frac{4}{7}×0.5\Bigg)\approx 0.46

よって、情報利得は

0.48-0.46= 0.02

次に以下のような分類をした場合の情報利得を求める。

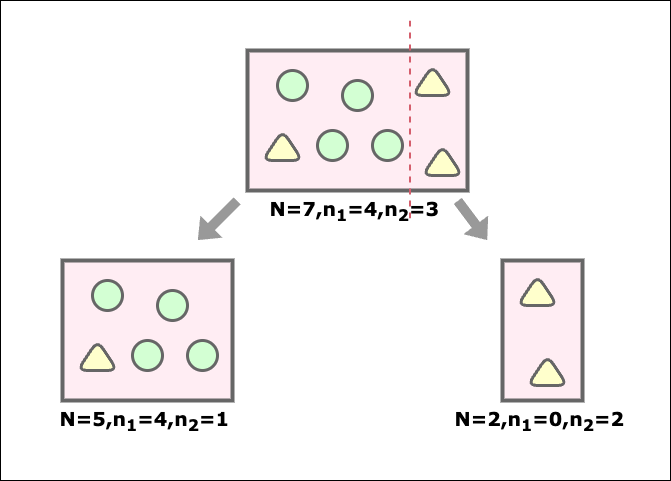
左子ノードの不純度は

1-\Bigg(\bigg(\frac{4}{5}\bigg)^2+\bigg(\frac{1}{5}\bigg)^2\Bigg)=0.32

右子ノードの不純度は

1-\Bigg(\bigg(\frac{0}{2}\bigg)^2+\bigg(\frac{2}{2}\bigg)^2\Bigg)=0

各グループの大きさを考慮するため、各子ノードの不純度に加重度をかける。

子ノードの加重平均 = \Bigg(\frac{5}{7}×0.32 + \frac{2}{7}×0\Bigg) \approx 0.22

よって、情報利得は

0.48-0.22 = 0.26

以上の結果から、情報利得の大きい後者の分類の方が良い分類だと判断できる。

2. エントロピー

エントロピーとはデータの不確実性を表す指標のこと。
データがどれだけごちゃごちゃしていて予測が難しいかを表す。

エントロピーが大きいほど、データの不確実性が高く予測しづらい(=不純度が高い)ということになる。

エントロピーは次の式で表すことができる。

H=\sum_{c=1}^{C}P(c)I(c)

• $P(c)$ : クラスcの比率(クラスcである確率)
• $I(c)$ : クラスcが出現した時の驚きの量(情報量)

$P(c)$を重みと捉えれば、すべてのクラスにおいてこの2つの量を掛け合わせたものの合計が驚きの期待値(平均的な驚き)となり、この値がエントロピーである。

また、$I(c)$は$P(c)$ を使って

I(c) = log_{2}\bigg(\frac{1}{P(c)}\bigg) = -log_{2}P(c)

と表すこともできるので、エントロピーは次のようにかける。

H=-\sum_{c=1}^{C}P(c)log_{2}P(c)

「-logP(c)＝驚きの量」を直感的に理解する

n個の中にクラスcのデータが1個あるとすると、$P(c)=\frac{1}{n}$である。

ここで、はい/いいえで答えられる質問(例：「前半にありますか？」)をして、選択肢を半分に絞りながら、どのデータがクラスcであるのかを当てるゲームをすると考える。

この時、何回の質問をする必要があるかを求める。

n=2の時、質問数は1
n=4の時、質問数は2
n=8の時、質問数は3
・・・
つまり、n=Nの時、質問数は $log_{2}N$ 回必要である。

ここで$P(c)=\frac{1}{N}$ つまり $N=\frac{1}{P(c)}$ なので

I(c) = -log_{2}P(c)

と表すことができる。

質問数が多い = 確率が低い = 驚きが大きいという関係が成り立つため、
$-\log_2 P(c)$が驚きの量(情報量)を表すことになる。

先ほどの例を使ってエントロピーを求める。

親ノードのエントロピーは、

P(\text{⚪︎}) = \frac{4}{7} \approx 0.571,　
P(\text{△}) = \frac{3}{7} \approx 0.429

であることから

-\left(\frac{4}{7}× \log_2 \frac{4}{7} + \frac{3}{7} × \log_2 \frac{3}{7}\right)= 0.985

左子ノードのエントロピーは、

P(\text{⚪︎}) = \frac{2}{3} \approx 0.667,　
P(\text{△}) = \frac{1}{3} \approx 0.333

であることから

-\left(\frac{2}{3} × \log_2 \frac{2}{3} + \frac{1}{3} × \log_2 \frac{1}{3}\right)= 0.918

右子ノードのエントロピーは、

P(\text{⚪︎}) = \frac{2}{4} = 0.5,　
P(\text{△}) = \frac{2}{4} = 0.5

であることから

-\left(\frac{2}{4} × \log_2 \frac{2}{4} + \frac{2}{4} × \log_2 \frac{2}{4}\right)= 1.0

子ノードのエントロピーの加重平均は、

\frac{3}{7} \times 0.918 + \frac{4}{7} \times 1.0=0.964

よって、情報利得は

0.985 - 0.964= 0.021

と計算できる。

コード

1. 学習の実行

決定木はsklearn.treeモジュールのDecisionTreeClassifierクラスのオブジェクトをモデルとして利用する。学習にはfit()に以下の引数を指定して実行する。

• max_depth : ツリーの深さを指定する(int)
• random_state : 乱数を固定する場合にシードを指定する(int)

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
data, target = iris.data, iris.target

X_train, X_test, y_train, y_test = train_test_split(data,target,test_size=0.3,random_state=123)

tree = DecisionTreeClassifier(max_depth=3, random_state=123)
tree.fit(X_train, y_train)

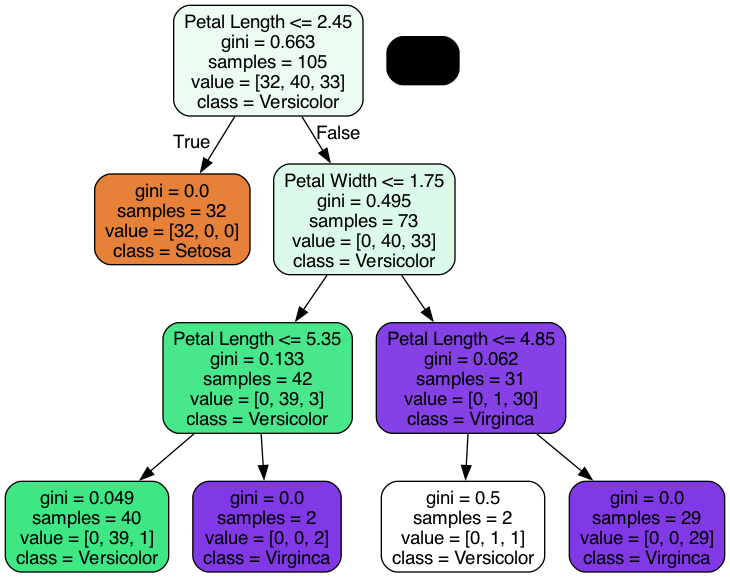
2. 決定木の可視化

2-1. 必要なツールをインストール

学習した決定議を可視化するには、グラフを描画するためのGraphvizをインストールして、それをpythonで使うためのpydotplusライブラリをインストールする。GraphvizはmacOSでHomebrewがインストールされていればbrewコマンドで、pydotplusはpipコマンドからインストールできるので、以下のコマンドをターミナルで実行する。

brew install Graphviz

pip install pydotplus

2-2. グラフの出力

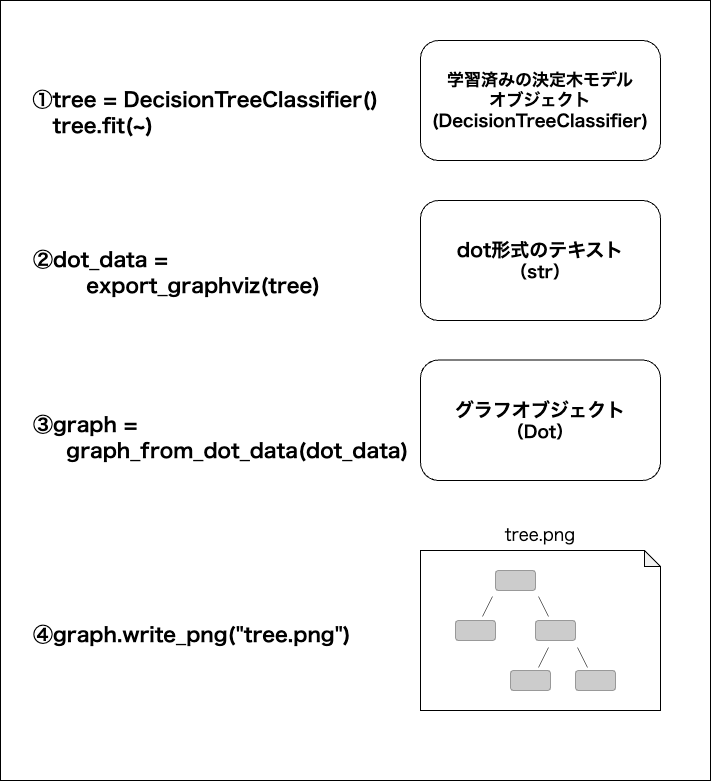
決定木を描画するには、sklearn.treeモジュールのexport_graphviz関数を使ってdot形式のデータを抽出してから、pydotplusモジュールのgraph_from_dot_data関数でグラフオブジェクトを取得してpngファイルに出力する。

export_graphviz関数の引数

引数名	内容
第1引数	学習済みのDecisionTreeClassifierオブジェクト
filled	Trueで指定するとノードの色分けをする クラスごとに色相(青とか赤とか)を変え、さらに純度によって色の濃さを変える(純度が高い＝色が濃い、純度が低い＝白に近づく)
rounded	Trueにするとノードの角を丸くする
class_names	分類するクラス名についての文字列リスト
feature_names	各特徴量の名前についての文字列リスト
out_file	出力するファイルのハンドル(ファイルハンドルオブジェクト)または名前(文字列) Noneを指定するとdot形式のテキストが文字列が返される

from sklearn.tree import export_graphviz
from pydotplus import graph_from_dot_data

dot_data = export_graphviz(tree,
                           filled=True,
                           rounded=True,
                           class_names=["Setosa","Versicolor","Virginca"],
                           feature_names=["Sepal Length","Sepal Width","Petal Length","Petal Width"],
                           out_file=None)

graph = graph_from_dot_data(dot_data)
graph.write_png("tree.png")

実行すると、以下のpngファイルが出力される。

ランダムフォレスト

複数の学習器を用いて学習することをアンサンブル学習といい、ランダムフォレストはそのアンサンブル学習のひとつ。

データや各特徴量をランダムに選択して、その各データ(ブートストラップデータ)から決定木を作成する処理を複数回繰り返し、その複数の決定木から得た推定結果で多数決を行ったりや平均値などを出して分類、回帰を行うという手法のこと。

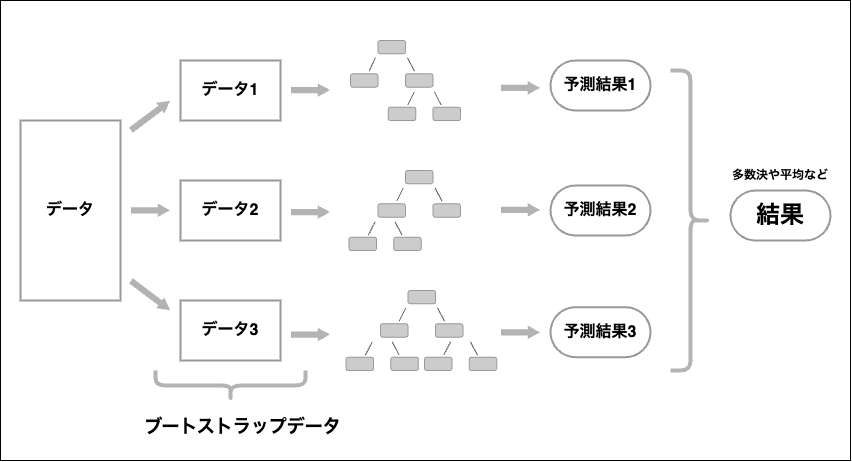
ランダムフォレストを実行するには、sklearn.ensembleモジュールのRandomForestClassifierクラスを利用する。

RandomForestClassifierクラスのコンストラクタ引数

引数名	内容
n_estimators	決定木の個数(int)
random_state	乱数のシードを固定する(int)

fit()メソッドに説明データと目的データをnumpy配列で渡すと、ランダムフォレストを実行し、学習済みの自身のオブジェクトを返す。また、predict()メソッドにテスト用の説明データを渡すと、モデルの予測結果をnumpy配列で取得できる。

先ほどのirisデータセットから分割したデータを使ってランダムフォレストの学習と予測を行うコードが以下。

from sklearn.ensemble import RandomForestClassifier

forest = RandomForestClassifier(n_estimators=100,random_state=123)
forest.fit(X_train,y_train)
y_pred = forest.predict(X_test)

実行結果

array([1, 2, 2, 1, 0, 1, 1, 0, 0, 1, 2, 0, 1, 2, 2, 2, 0, 0, 1, 0, 0, 1,
       0, 2, 0, 0, 0, 2, 2, 0, 2, 1, 0, 0, 1, 1, 2, 0, 0, 1, 1, 0, 2, 2,
       2])