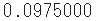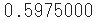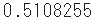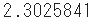損失関数(loss function)
- 損失関数をはじめ、誤差関数、コスト関数などと、いくつか呼び名があります。
- 最適な重みパラメータにたどりつくために、一つの指標を手がかりにして計算をくりかえす。その指標のことです。
- 一般に2乗和誤差や交差エントロピー誤差が用いられます。
- 誤差という、性能の悪さを示す指標ですが、モデルはそれがなるべく小さくなるような重みパラメータを見つけます。
2乗和誤差(mean squared error)
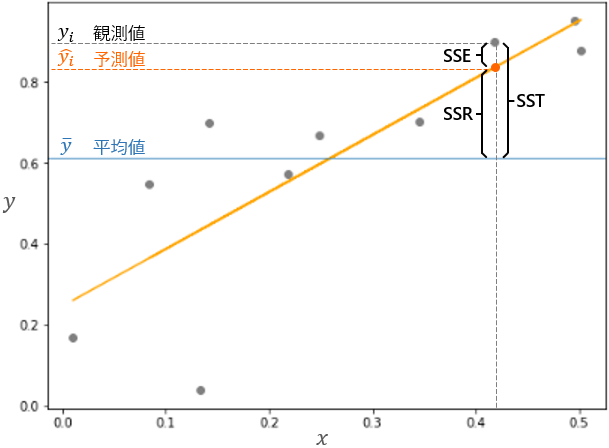
- **2乗和誤差(またの名をsum of squares error:SSE)**とは、予測値と観測値との差の2乗を合計したものです。
- 実際に観測されたデータの平均値を基準として、**観測値全体の変動(sum of squares total:SST)から、回帰による予測値全体の変動(sum of squares regression:SSR)**をひいたもの、ともいえます。
2乗和誤差、交差エントロピー誤差関数を実装してみる
- 次のように、出力を2ケースと、正解にあたる教師データを仮定します。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 教師データ | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 出力1 | 0.1 | 0.05 | 0.6 | 0.0 | 0.05 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 |
| 出力2 | 0.1 | 0.05 | 0.1 | 0.0 | 0.05 | 0.1 | 0.0 | 0.6 | 0.0 | 0.0 |
- 教師データは、1,0型データで「2」を正解とします。出力の方は、たとえば出力1の場合、「0」の確率は0.1、「1」の確率は0.05、「2」の確率は0.6で最も高くなっています。また、出力2では「7」の確率が0.6で最も高く、つまり出力1と2とで「2」と「7」の確率が入れ替わっています。
- 2乗和誤差関数の数式を示します。
- $\displaystyle E = \frac{1}{2} \sum_{k}(y_{k} - t_{k})^2$
- $k$はデータの次元数、$y_{k}$はモデルが出力した値、$t_{k}$は教師データの値を表します。
⑴ ライブラリのインポート
# データ加工・処理・分析ライブラリ
import numpy as np
import numpy.random as random
import pandas as pd
# 可視化ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline
# 小数第3位まで表示
%precision 7
⑵ 2乗和誤差関数の定義と実行
# 2乗和誤差関数の定義
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
# 教師データの設定
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# 出力1の設定:「2」の確率が最も高い
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 出力1の2乗和誤差を算出
mean_squared_error(y, t)
# 出力2の設定:「7」の確率が最も高い
y = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0])
# 出力2の2乗和誤差を算出
mean_squared_error(y, t)
- 出力1の2乗和誤差は0.0975000、出力2の2乗和誤差は0.5975000で、正解の「2」の確率の高い出力1の方がずっと小さい値になっています。
- 2乗和誤差の値が小さければ小さいほど、教師データに適合していることがわかります。
交差エントロピー誤差(cross entropy error)
- 交差エントロピー誤差関数の数式を示します。
- $\displaystyle E=-\sum_{k}t_{k}\log{y_{k}}$
- 2乗和誤差と同じく、$k$はデータの次元数、$y_{k}$はモデルが出力した値、$t_{k}$は教師データの値を表します。
- この$log$は、底を$e$とする自然対数$log_{e}$を表わしています。
⑶ 交差エントロピー誤差関数の定義と実行
# 交差エントロピー誤差関数の定義
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
- 数式の通りなら
return -np.sum(t * np.log(y))のはずなのに、deltaというごく微小な定数(1e-7 = 0.0000001)を$y$に足しています。 - これは、計算をくり返していく中で、もし$y=0$が発生した場合、np.log(0)はマイナスの無限大となって、一つの値に定まらないため計算がそれ以上進められなくなります。そこで、微小な値を足して、その防止策としています。
# 教師データの設定
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# 出力1の設定:「2」の確率が最も高い
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 出力1の交差エントロピー誤差を算出
cross_entropy_error(y, t)
# 出力2の設定:「7」の確率が最も高い
y = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0])
# 出力2の交差エントロピー誤差を算出
cross_entropy_error(y, t)
- 出力1の交差エントロピー誤差は0.5108255、出力2の方は2.3025841で、やはり正解の「2」の確率の高い出力1の方がずっと小さい値になっています。
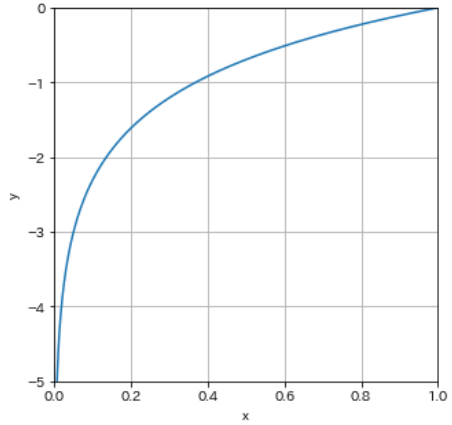
- ここで改めて、自然対数$y=log_{x}$のグラフを描いてみます。
# 等差数列の生成
x = np.linspace(0, 1, 1000)
# 対数関数を定義
y = np.log(x) # 底をeとする対数関数
plt.figure(figsize=(5,5))
plt.xlim([0.0, 1.0])
plt.ylim([-5, 0])
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.plot(x, y)
-
numpy.linspace(start, stop, num)は、startの値からstopの値までの間をnumの数で等間隔に分けた配列を返します。 - numpyには、対数関数として以下の4つがあります。
-
log(x):底を$e$とする$x$の対数 -
log2(x):底を$2$とする$x$の対数 -
log10(x):底を$10$とする$x$の対数 -
log1p(x):底を$e$とする$x+1$の対数
-
- xが1のときyは0になり、xが0に近づくにつれてyの値は小さくなります。交差エントロピー誤差の式は、マイナスをかけて正負を逆転しますので、yの値が小さくなるほど誤差の値は大きくなります。
「底をeとする自然対数log」とは?
- まずは指数、たとえば$10^4=10000$は、いうまでもなく「10を4乗すると10000になる」ということ。この逆が対数です。
- たとえば、${log_{10}}^{10000}$ は「10000は10を何乗した数か?」「答えは4乗」ということで、このとき$10$を対数の**底(てい)**といいます。
- 実際、対数の底というのは、10(常用対数)か 、$e$(自然対数)がほとんどです。
- そこで**「$e$」**ですが、ネイピア数とかネピア数、オイラー数などの名で呼ばれ、いわば円周率みたいなもの、自然界の掟というような存在です。
- 具体的な数字で示すと、$e = 2.71828 18284 59045 23536 02874 71352 …$というぐあいに無限につづきます。
- これが非常に珍しい性質をもっています。ネイピア数を底とした関数を微分しても同じ関数に戻る、すなわち$\displaystyle \frac{e^x}{dx}=e^x$というものです。
- この特質がゆえに、物理や化学、生物学など、あらゆる事象について微分方程式をつかって記述する上では、$e$は欠かすことのできない存在とされています。
- つまり、交差エントロピー誤差の数式 $\displaystyle E=-\sum_{k}t_{k}\log{y_{k}}$ では、$log_{yk}$すなわち「出力された値は$e$を何乗した数か?」を用いています。
- $e$(ネイピア数)は、円周率$π$のようにイメージがしやすいものではないので、なんとなくもやもやした感じが拭えないのですが、かといって$π$を疑ってかかったこともないわけで、〝円周率のようなもの〟としてそれ以上深入りしないことにしています。