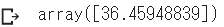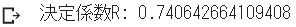機械学習ライブラリに頼らず、数値計算に必要なNumpyとPandasだけを用いて、重回帰分析のしくみを学びます。
重回帰分析の方程式は、目的変数$y$に対し説明変数$x_{i}$が$n$個のあるとき、次のように表わされます。

目的とする変数$y$を、$x_{1}, x_{2}, x_{3}, ..., x_{n}$という$n$個の変数で説明しています。
偏回帰係数$a_{1}, a_{2}, a_{3}, ..., a_{n}$と切片$a_{0}$は定数(一定の数字)であり、偏回帰係数は説明変数それぞれの加重(いわば変数$y$への影響度)を表わし、それで説明しきれない部分が切片となります。
つまり偏回帰係数$a_{1}, a_{2}, a_{3}, ..., a_{n}$と切片$a_{0}$を求めることが重回帰分析の目標です。
(単回帰分析では単回帰係数というのに対し、重回帰分析では偏回帰係数と呼びます)
重回帰分析において最もシンプルな3つの変量を扱う場合、つまり目的変数$y$を2つの変数$x_{1}, x_{2}$で説明する場合の重回帰式を図示します。
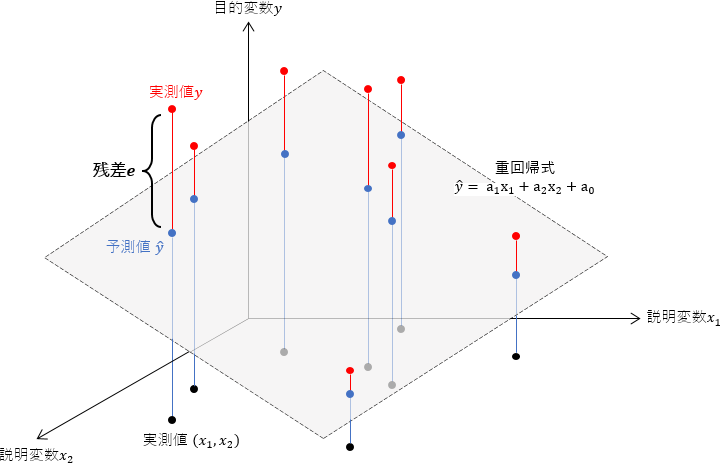
3次元の立体空間は、説明変数$x_{1}, x_{2}$の2軸からなる2次元平面を底面として、これに対して目的変数の$y$軸が垂直に交わっています。
この空間内に浮かんだような斜面として重回帰式が表わされています。
これは、実測値$(x_{1}, x_{2})$との関係にもとづいて、実測値$y$(●)の散らばりを要約したものということができます。
さて、実測値として$(x_{1}, x_{2}, y)$があり、また重回帰式により$(x_{1}, x_{2})$が与えられると予測値$\hat{y}$(●)が定まります。
このとき、実測値$y$(●)と予測値$\hat{y}$(●)のあいだに誤差が生じます。
これを残差と称し、残差$e$が全体として最も小さくなるように偏回帰係数と切片を求めます。
すなわち単回帰分析と同じく最小二乗法を利用します。
⑴ ライブラリをインポートする
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
⑵ データを読み込む
from sklearn.datasets import load_boston
boston = load_boston()
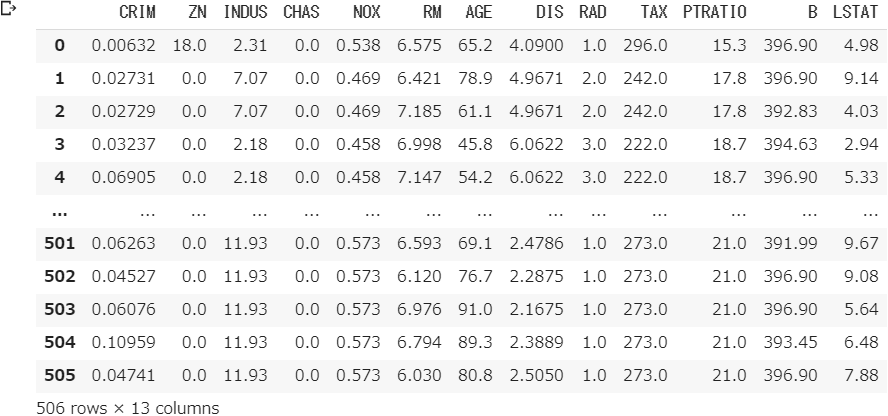
⑶ 目的変数をデータフレームに変換する
boston_df_ob = pd.DataFrame(boston.target, columns=["PRICE"])
boston_df_ob
⑷ 説明変数をデータフレームに変換する
boston_df_ex = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_df_ex
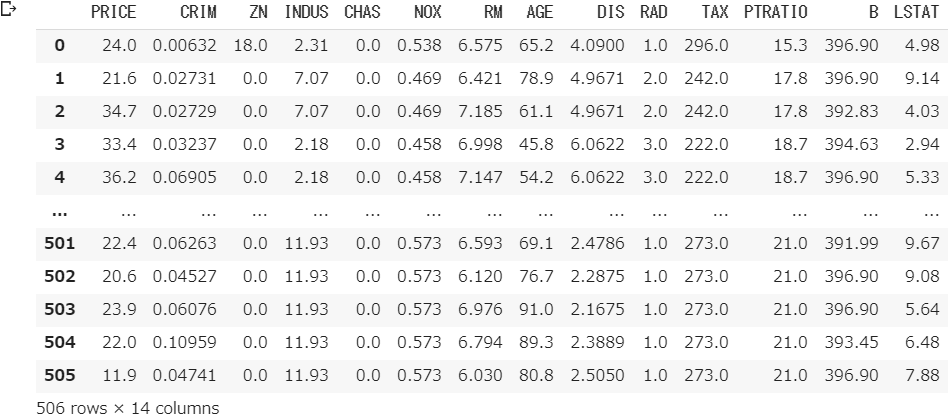
⑸ 目的変数と説明変数を統合する
boston_df = pd.concat([boston_df_ob, boston_df_ex], axis=1)
boston_df
残差の定義
3変量を扱う場合、重回帰式は次のように表わすことができます。
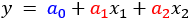
この方程式にもとづいて、残差を下表の最右列に示します。
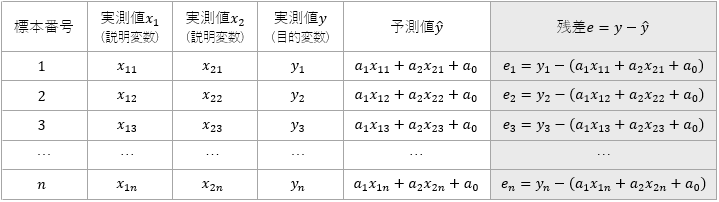
標本ごとの残差$e$には正負があるため、そのまま合計すると相殺されて 0 になってしまいます。そこで、各標本の残差を2乗し、全体の残差を次のように定義します。
$Q = {e_{1}}^{2}+{e_{2}}^{2}+{e_{3}}^{2}…+{e_{n}}^{2}$
この残差平方和 $Q$ が最小になるように偏回帰係数と切片を求めます。
偏微分
残差平方和$Q$ が最小になるとき、偏回帰係数 $a_{0}, a_{1}, a_{2}$ は次の条件を満たします。
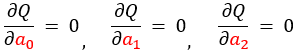
要するに、すべての係数が偏微分すると 0 になる。$∂$(デル)は偏微分を表わす記号です。
微小に分けると書いて微分、微小に分けてみたときの変化のしかたを問題にするのが微分です。微小にずらしてみたら結果は $0$、すなわち変化していない。つまり傾きが $0$ ということはそれ以上小さくなることはない。したがって最小とみなされます。
偏微分とは、多変量からなる関数において特定の「文字」に注目し、それ以外はすべて定数(数字)とみなすというものです。
残差平方和$Q$ は、$a_{0}, a_{1}, a_{2}$ という3つの文字を含みます。
たとえば $a_{1}$以外は定数とみなし、関数$Q$を $a_{1}$で微分した結果が $0$ になる。同じく $a_{0}$ でも $a_{2}$ でも微分して $0$ になるとき残差は最小となります。
重回帰分析の公式
先の3つの条件式をそれぞれ変形して、偏回帰係数と切片を計算する連立方程式に直します。
まず、切片$a_{0}$の条件を定めた式、
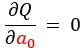
これを展開し、まとめ直すと、次の式が得られます。
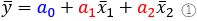
$\bar{y}$は$y$の平均値、$\bar{x_{1}}, \bar{x_{2}}$も同じくそれぞれの平均値を表わします。この①式が、切片$a_{0}$を求める公式になります。
次に、偏回帰係数 $a_{1}, a_{2}$ それぞれの条件を定めた式、
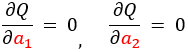
これらの式を展開し変量ごとにまとめると、次の2つの式が得られます。
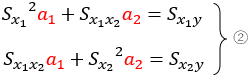
②は偏回帰係数$a_{1}, a_{2}$を求める公式であり、①②の連立方程式を解くことで偏回帰係数と切片を得ることができます。
また、②の2つの式は、行列として1つにまとめることができます。
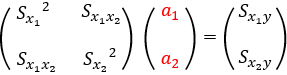
係数$a_{1}, a_{2}$をくくり出し、左辺を2つの行列の乗算に置き換えました。
分散共分散行列
ここで改めて、変量が$n$個の場合の重回帰式を示します。
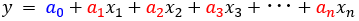
目的変数を$y$とし、$n$個の説明変数は$x_{1}, x_{2}, x_{3}, ..., x_{n}$、それらの偏回帰係数は$a_{1}, a_{2}, a_{3}, ..., x_{n}$、また切片は$a_{0}$となっています。
このとき、偏回帰係数と切片を求める方程式は、先の①②にならって次のように表わされます。

④式に注目します。左辺の左側の行列は、説明変数$x_{1}, x_{2}, x_{3}, ..., x_{n}$の分散共分散行列になっています。
対角成分が変数ごとの分散 ${Sx_{1}}^2, {Sx_{2}}^2, {Sx_{3}}^2, ..., {Sx_{n}}^2$ になっており、これを挟んで上三角行列と下三角行列は対称をなし、たとえば $S_{x_{1}x_{2}}, S_{x_{1}x_{3}}, ..., S_{x_{1}x_{n}}$ というように変数2種類一組ごとの共分散になっています。
共分散(Cov)は、二組の対応するデータ間の関係を表わす指標です。
たとえば$n$組のデータ$(x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3}),
..., (x_{n}, y_{n})$があるとき、共分散は次式に表わされます。
$s_{xy} = \frac{1}{n - 1} \displaystyle \sum_{i = 1}^n
{(x_i - \overline{x})(y_{i} - \overline{y})}$
「($x$の偏差 × $y$の偏差) の平均」と定義され、次のように解釈されます。
・共分散の値が正の場合、$x$が大きいとき$y$も大きい傾向がある。
・共分散の値が$0$に近い場合、$x$と$y$にはあまり関係がない。
・共分散の値が負の場合、$x$が大きいとき$y$は小さい傾向がある。
さて、偏回帰係数と切片を求める重回帰分析の方程式を導きます。
③、④式をさらに変形し、ターゲットである切片$a_{0}$および係数$a_{1}, a_{2}, a_{3}, ..., a_{n}$を左辺に出します。

つまり④式の両辺を、分散共分散行列で割って⑥式になりました。⑥式の右辺に現れた分散共分散行列は、右肩に「-1」がついて、これは逆行列であることを意味しています。
逆行列
逆行列は、数字の「逆数」と同じような働きをする行列です。
そもそも逆数とは、たとえば $3$ の逆数は$\frac{1}{3}$、$19$ の逆数は$\frac{1}{19}$ですが、これを元の数字にかけると結果は $1$ になります。
$3×\frac{1}{3}=1$ $19×\frac{1}{19}=1$
行列の計算において、この数字の $1$ に相当するものを単位行列といいます。
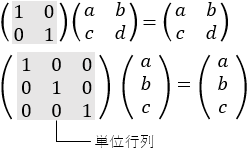
対角成分が$1$、非対角成分が$0$という行列で、単位行列にどのような行列$A$をかけても$A$は変化しません。
さて逆行列は、ちょうど数字の逆数のように、ある行列にその逆行列をかけると結果は単位行列になるという働きをします。
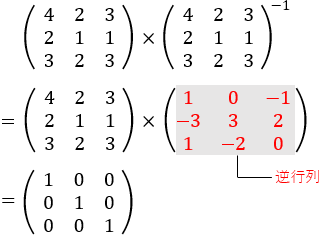
たとえば、次のような行列があるとします。

その逆行列をかけてやると結果は単位行列になります。
⑹ Numpyの多次元配列arrayに変換する
boston_arr = np.array(boston_df)
print(boston_arr)
⑺ 分散共分散行列を算出する
cov = np.cov(boston_arr, rowvar=0, bias=0)
print(cov)

Numpyのcov関数によって「分散共分散行列」を算出しました。
この2次元配列には、次の表のような形状で分散・共分散の値が入っています。

偏回帰係数を求める⑥式において右辺の左側にあたるのが薄い青色の部分ですが、これは逆関数に変換する前のもとの分散共分散行列です。
また、薄い赤色の部分は同じく右辺の右側にあたり、目的変数$y$と説明変数$x_{i}$の共分散行列になっています。
では便宜的に、前者の分散共分散行列を行列$A$、後者の共分散行列を行列$B$と呼びます。
⑻ 偏回帰係数を計算する
# 分散共分散行列Aを作成
covA = cov[1:, 1:]
# 共分散行列Bを作成
covB = cov[1:, 0] # 1×13
covB = covB.reshape(13, 1) # 13×1の2次元配列に変換
# 分散共分散行列Aを逆行列に変換
covA_inv = np.linalg.inv(covA)
# 偏回帰係数を計算
coef = np.dot(covA_inv, covB)
print(coef)
分散共分散行列$cov$から行列$A$、行列$B$にあたる部分を取り出して、それぞれ変数covA covBとして格納します。
その際、行列$B$は取り出したままでは (1, 13) の1次元配列なので、reshape関数で (13, 1) の2次元配列に変換して後の計算に備えます。
次いで逆行列をNumpyのlinalg.inv関数で求めます。ちなみにinvは逆関数inverse function の略です。
さて、分散共分散の逆行列に共分散行列をかけて偏回帰係数を計算します。すなわち、Numpyのdot関数でcovA_invとcovBの内積を求めます。

内積
かりに、数字のかけ算のように行列同士を乗算すると、
covA_inv * covB
計算結果は (13, 13) の行列となります。
次のように、左側の行列のヨコと右側の行列のタテとで対応する値同士の乗算となるからです。
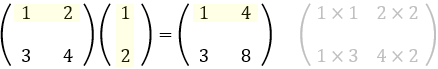
一方、内積をとると、
np.dot(covA_inv, covB)
計算結果は (13, 1) の行列となり、説明変数$x_{i}$のそれぞれについて1個ずつの数値データとなっています。
次のように、同じく対応する値同士の乗算を、さらにそれぞれ和算した値を算出しているからです。
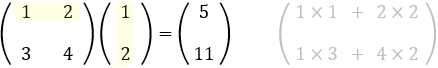
⑼ 切片を計算する
切片を求める計算式を再掲します。
$a_{0} = \overline{y} - a_{1}\overline x_1 - a_{2}\overline x_2 - a_{3}\overline x_3 - ... - a_{n}\overline x_n$
# 説明変数それそれの平均値
x_mean = np.mean(boston_arr[:, 1:], axis=0)
# (回帰係数 × 説明変数) の総和
sum = 0
for i,j in zip(coef, x_mean):
sum += i * j
# 目的変数の平均値から説明変数項の総和をひく
np.mean(boston_arr[:, 0]) - sum
⑽ 決定係数を計算する
こうして得られた重回帰式の精度を確認します。
重回帰式による予測値$\hat{y}$の分散が、実測値$y$の分散に対して何パーセントにあたるか、すなわちどの程度もとの変量を説明できているかを計算します。
## 予測値y_hatの分散を求める
# 説明変数xのみの行列を取得
X = boston_arr[:, 1:]
# 変数毎に偏回帰係数を乗算し、切片を加算
coef2 = np.reshape(coef, [1, 13])
Y_hat = np.sum(X * coef2, axis=1) + intercept
# 予測値y_hatの分散
np.var(Y_hat)
## 実測値yの分散を求める
# 目的変数yのみの行列
Y = boston_arr[:, 0]
# 実測値yの分散
np.var(Y)
# 決定係数を計算する
R = np.var(Y_hat) / np.var(Y)
print("決定係数R:", R)
先のscikit-learnによる分析結果に照らして、自前の計算による結果も同じ値を示していることが確認されました。
ここまで見て来たように、回帰分析はある結果に影響を与えていると考えられる変量の一つひとつに関心を向ける分析方法でした。
これとは対照的に、変量の一つひとつを独立的に扱うのではなく、総合的に取り扱う分析方法、主成分分析を学びます。