LoginSignup
3
4

More than 1 year has passed since last update.

@y_itoh(yumi ito)

1. Pythonで学ぶ統計学　2-4. 統計用語の基本

Posted at

統計学の用語には文字面の似通ったものが多く紛らわしいので、ここで改めて、特に平均と分散に関する主な用語についてまとめます

基本的な統計量

種別 用語 対象 記号・表記 略意
平均 ➀平均値 資料 $\overline{x}$ 資料の平均値
➁標本平均 標本 $\overline{X} \hspace{5px}$, $M$ 標本の平均値
➂母平均 母集団 $μ$ 母集団の平均値
➃期待値 確率分布 $μ$, $E(X)$ 予測値としての平均値
分散 ➄母分散 母集団 $σ^2$ 母平均への集中度
➅標本分散 標本 $s^2$ 標本平均への集中度
➆確率変数の分散 確率分布 $σ^2$, $V(X)$ 期待値への集中度

➀平均値(mean)

  • 一定の属性をもつ数値データ群の平均値
  • データの「ちらばりの重心」を示し、下式で定義されるとおりデータの総和をデータ数で割ったもの
  • $ \displaystyle \overline{x} = \frac{1}{N} \sum_{i=1}^{N} x_{i} = \frac{x_{1} + x_{2} +…+ x_{N}}{N} $
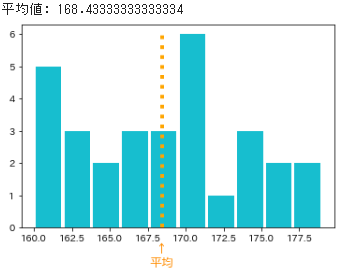
  • 都内のある高校で3年生のクラスの男子生徒30名の身長を測定したと仮定して乱数を生成し、そのヒストグラムと平均値を以下に示します

image.png

➁標本平均(sample mean)

  • 母集団から無作為抽出された標本データの平均値を「標本平均」といいます
  • 前項の平均値と混同されやすいので要注意です
  • $ \displaystyle \overline{X} = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \frac{X_{1} + X_{2} +…+ X_{n}}{n} $
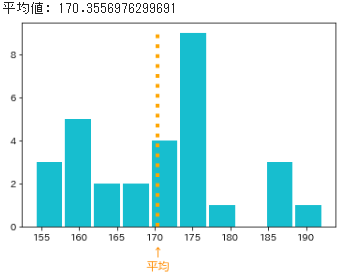
  • 都内の高校3年生の男子生徒を母集団として、無作為に30人を抽出したと仮定して乱数を生成し、そのヒストグラムと平均値（標本平均）を以下に示します

image.png

  • 先の「平均値」とは異なり、こちらは都内の高3男子生徒の全体（母集団）の縮図となっています
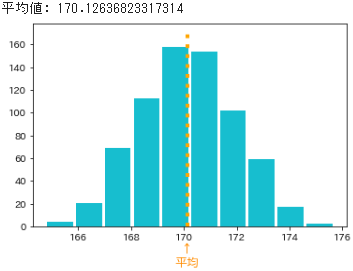
  • さらに、標本抽出（サンプリング）を700回くり返したと仮定し、そこで得られた700通りの標本平均の分布とそれらの平均値を以下に示します
  • 標本平均は確率変数なので、その分布は「確率分布」であり、正規分布になります

image.png

➂母平均(population mean)

  • 母集団の平均値を「母平均」といいます
  • 母集団は集計分析の対象となる集合全体のことで、標本を抽出するときのもとの集団にあたります
  • 真に知りたいのはこの母平均なわけですが、これがわからないので「標本平均」で代用します
  • 従って、標本数が増えると、標本平均は少しずつ「母平均」に近づいていくことになります
  • $ \displaystyle μ = \frac{1}{N} \sum_{i=1}^{N} x_{i} = \frac{x_{1} + x_{2} +…+ x_{N}}{N} $
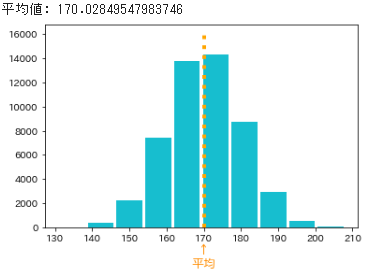
  • 都内の高校3年生の男子生徒は50,440人なので、その全員の身長を測定したと仮定して乱数を生成し、その分布と平均値（母平均）を以下に示します

image.png

➃期待値(expectation)

  • 期待値と平均値はしばしば混用されますが、実際まだ手に入れていない未知のデータの平均値（予想値）を「期待値」といいます
  • 確率変数はいろいろの値をとり得るわけですが、それらを代表する平均値のことであって、正確には「確率の重みつき平均」です
  • 個人的な信念や勘などに依拠しない客観的な予測値ともいえます
  • $離散型確率変数: \displaystyle E(X) = \sum_{i=1}^{n} x_{i} p_{i} $
  • $連続型確率変数: \displaystyle E(X) = \int_{-\infty}^{\infty} xf(x)dx $
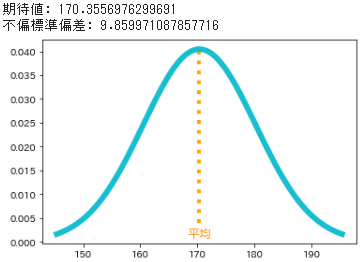
  • 先の標本 $n=30$ における平均（標本平均＝期待値）および分散を用いた確率密度関数を以下に示します

image.png

  • 定義上、標本においては平均値と期待値はまったく同じになります
  • 統計とは半面、既知の一部から未知の全体を推定する取り組みといえます

➄母分散(population variance)

  • 母集団の分散
  • 分散は、データが平均値を中心としてどれくらい散らばっているかを表す指標です
  • $ \displaystyle σ^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - μ)^2 = \frac{(x_{1} - μ)^2 + (x_{2} - μ)^2 +…+ (x_{n} - μ)^2}{n} $
  • 母分散は上式に定義されますが、そもそも母集団は未知のデータですから、母分散 $ σ^2 $ は標本分散 $ s^2 $ に近似されるという想定のもとに、標本分散で母分散を推定しますが･･･
  • 「都内の高校3年生の男子全体」という母集団を仮定し、母分散$σ^2$及びその平方根にあたる母標準偏差$σ$を求めてみましょう
# 母集団を仮定し、母分散を取得
np.random.seed(seed=0) # 乱数を固定
population = np.random.normal(loc = 170, scale = 10, size = 50440) # 平均μ=170, 標準偏差σ=10

# 母平均
population_av = np.mean(population)
print("母平均:", population_av)

# 母標準偏差
population_std = np.std(population, ddof=0) # 標準偏差
print("母標準偏差:", population_std)

# 母分散
print("母分散:", population_std ** 2)

image.png

➅標本分散(sample variance)

  • 標本分散は、標本データが標本平均（期待値）を中心にどれくらい散らばっているかを表す指標です
  • ただし、標本分散 $ S^2 $ の値は、母分散と比べて過小評価になるという偏りがありますので、これを修正した不偏分散(unbiased variance) $ s^2 $ を用います
  • $不偏分散: \displaystyle s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_{i} - μ)^2 = \frac{(x_{1} - \overline{x})^2 + (x_{2} - \overline{x})^2 +…+ (x_{n} - \overline{x})^2}{n-1} $
  • $標本分散: \displaystyle S^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - μ)^2 = \frac{(x_{1} - \overline{x})^2 + (x_{2} - \overline{x})^2 +…+ (x_{n} - \overline{x})^2}{n} $
  • 先に仮定した母集団から無作為に30人を抽出し、不偏標準偏差と標準偏差を取得してみます
# 母集団から無作為に30人を抽出
import random
random.seed(5)

sample = []
for i in range(30):
    value = random.choice(population)
    sample.append(value)
print(sample)
print(len(sample))

# 標本平均
sample_av = np.mean(sample)
print("標本平均:", sample_av)

# 標本標準偏差
sample_std = np.std(sample, ddof=1) # 不偏標準偏差
print("不偏標準偏差:", sample_std)
sample_std_unbiase = np.std(sample, ddof=0) # 標準偏差
print("( 標準偏差:", sample_std_unbiase,")")

# 標本分散
print("標本分散:", sample_std ** 2)

image.png

➆確率変数の分散(variance)

  • 確率分布が与えられたとき、下式で算出される値が「確率変数の分散$σ^2$」（標準偏差は$σ$）になります
  • $離散型確率変数: \displaystyle V(X) = \sum_{i=1}^{n} (x_{i} - μ)^2 p_{i} \hspace{5px}$

  • $連続型確率変数: \displaystyle V(X) = \int_{-\infty}^{\infty} (x - μ)^2 f(x)dx $

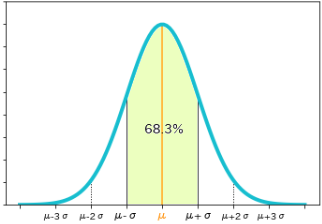
  • 確率変数$X$が、期待値$μ$を中心として$μ-σ≦X≦μ+σ$の範囲内の値をとる確率は 68.3%(0.6827) です

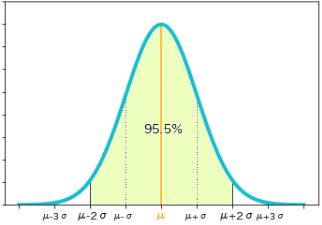
image.png

  • 同じく確率変数$X$が$μ-2σ≦X≦μ+2σ$の値をとる確率は 95.5%(0.9545)

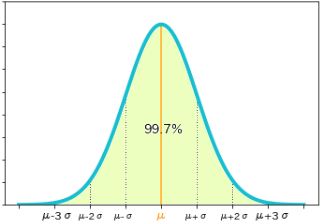
image.png

  • 同じく確率変数$X$が$μ-3σ≦X≦μ+3σ$の値をとる確率は 99.7%(0.9973) で、これを3シグマ範囲といいます
  • この区間外に落ちる確率はほぼ3/1000ですから、つまり3シグマ範囲は事実上すべて（全体の確率=1）に相当します

image.png

Appendix

# 数値計算ライブラリ
import numpy as np
from scipy import stats

# グラフ描画ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline

# matplotlibの日本語表示対応モジュール
!pip install japanize-matplotlib
import japanize_matplotlib

➀平均値(mean)

# 都内のある高校で3年生のクラスの男子生徒30名の身長を測定したと仮定

# 任意の範囲で乱数を生成
np.random.seed(3) # 乱数を固定
height_data = np.random.randint(low = 160, high = 180, size = 30)

# 平均値を取得
ave = np.mean(height_data)
print("平均値:", ave)

# グラフ描画
plt.hist(height_data, color = 'tab:cyan', rwidth = 0.9)
plt.vlines(x=ave, ymin=0, ymax=6, color="orange", lw=4, linestyle=':')
plt.text(ave, -1.2, '↑\n平均', fontsize = 13, horizontalalignment='center', color="darkorange")
plt.show()

➁標本平均(sample mean)

# 都内の高校3年生の男子生徒を母集団として、無作為に30人を抽出したと仮定

# 正規分布に従う乱数を生成
np.random.seed(4) # 乱数を固定
sample_data = np.random.normal(loc = 170, scale = 10, size = 30) # 平均μ=170, 標準偏差σ=10

# 平均値を取得
sample_mean = np.mean(sample_data)
print("平均値:", sample_mean)

# グラフ描画
plt.hist(sample_data, color = 'tab:cyan', rwidth = 0.9) # ヒストグラムを描画
plt.vlines(x=sample_mean, ymin=0, ymax=9, color="orange", lw=4, linestyle=':') # 平均の垂直線
plt.text(sample_mean, -2, '↑\n平均', fontsize = 13, horizontalalignment='center', color="darkorange") # テキストの挿入
plt.show()

# 標本抽出（サンプリング）を700回くり返したと仮定

samples = []
sample_averages = []

for i in range(700):
    np.random.seed(i) # 乱数を固定
    X = np.random.normal(loc = 170, scale = 10, size = 30)
    samples.append(X)
    average = np.mean(X)
    sample_averages.append(average)
print(sample_averages)

# 平均値を取得
ave = np.mean(sample_averages)
print("平均値:", ave)

# グラフ描画
plt.hist(sample_averages, color = 'tab:cyan', rwidth = 0.9)
plt.vlines(x=ave, ymin=0, ymax=170, color="orange", lw=4, linestyle=':')
plt.text(ave, -35, '↑\n平均', fontsize = 13, horizontalalignment='center', color="darkorange")
plt.show()

➂母平均(population mean)

# 都内の高校3年生の男子生徒50,440人全員の身長を測定したと仮定

# 正規分布に従う乱数を生成
np.random.seed(seed=5) # 乱数を固定
population = np.random.normal(loc = 170, scale = 10, size = 50440) # 平均μ=170, 標準偏差σ=10

# 平均値を取得
ave_p = np.mean(population)
print("平均値:", ave_p)

# グラフ描画
plt.hist(population, color = 'tab:cyan', rwidth = 0.9)
plt.vlines(x=ave_p, ymin=0, ymax=16000, color="orange", lw=4, linestyle=':')
plt.text(ave_p, -3300, '↑\n平均', fontsize = 13, horizontalalignment='center', color="darkorange")
plt.show()

➃期待値(expectation)

# 標本n=30における平均(標本平均＝期待値)および分散を用いた確率密度関数

from scipy import stats

# 期待値・標準偏差を指定
mu = np.mean(sample_data)
sigma = np.std(sample_data, ddof=1) # 不偏標準偏差
print("期待値:", mu)
print("不偏標準偏差:", sigma)

# 等差数列を生成
arithmetic_progression = np.linspace(mu-25, mu+25, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=arithmetic_progression, loc=mu, scale=sigma) # loc=期待値, sigma=標準偏差
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値

# グラフ描画
plt.plot(arithmetic_progression, norm_pdf, lw=6, color="tab:cyan")
plt.vlines(x=mu, ymin=0.004, ymax=norm_pdf_max, color="orange", lw=4, linestyle=':')
plt.text(mu, 0.001, '平均', fontsize = 13, horizontalalignment='center', color="darkorange")

plt.show()

➆確率変数の分散(variance)

# 所与の確率分布を仮定（1σ範囲）

# 所与の期待値と分散
mu = 0
variance = 1

# 期待値と分散(標準偏差)をもとに確率密度関数を生成
data_2 = np.linspace(mu-4, mu+4, 100)
sigma = np.sqrt(variance)
norm_pdf = stats.norm.pdf(x = data_2, loc = mu, scale = sigma)

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower_1 = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) # 確率変数μ-σ
upper_1 = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) # 確率変数μ+σ
lower_2 = stats.norm.pdf(x=mu-2*sigma, loc=mu, scale=sigma) # 確率変数μ-2σ
upper_2 = stats.norm.pdf(x=mu+2*sigma, loc=mu, scale=sigma) # 確率変数μ+2σ
lower_3 = stats.norm.pdf(x=mu-3*sigma, loc=mu, scale=sigma) # 確率変数μ-3σ
upper_3 = stats.norm.pdf(x=mu+3*sigma, loc=mu, scale=sigma) # 確率変数μ+3σ

# 確率密度関数のグラフを描画
plt.plot(data_2, norm_pdf, color = "tab:cyan", lw = 4)

# 垂直線
plt.vlines(x=mu, ymin=0, ymax=norm_pdf_max, color="orange", lw=1.5) # μ
plt.vlines(mu-sigma, 0, lower_1, color="black", lw=0.8) # μ-σ
plt.vlines(mu+sigma, 0, upper_1, color="black", lw=0.8) # μ+σ
plt.vlines(mu-2*sigma, 0, lower_2, color="black", lw=1, linestyle=':') # μ-2σ
plt.vlines(mu+2*sigma, 0, upper_2, color="black", lw=1, linestyle=':') # μ+2σ
plt.vlines(mu-3*sigma, 0, lower_3, color="black", lw=1, linestyle=':') # μ-3σ
plt.vlines(mu+3*sigma, 0, upper_3, color="black", lw=1, linestyle=':') # μ+3σ

# テキストを配置
plt.text(mu-0.2, -0.03, 'μ', fontsize = 13, color = "darkorange") # μ
plt.text(mu-sigma-0.4, -0.03, 'μ-σ', fontsize = 12) # μ-σ
plt.text(mu+sigma-0.4, -0.03, 'μ+σ', fontsize = 12) # μ+σ
plt.text(mu-2*sigma-0.4, -0.03, 'μ-2σ', fontsize = 10) # μ-2σ
plt.text(mu+2*sigma-0.4, -0.03, 'μ+2σ', fontsize = 10) # μ+2σ
plt.text(mu-3*sigma-0.4, -0.03, 'μ-3σ', fontsize = 10) # μ-3σ
plt.text(mu+3*sigma-0.4, -0.03, 'μ+3σ', fontsize = 10) # μ+3σ
plt.text(mu-0.5, 0.16, '68.3%', fontsize = 14) # 68.3%

# 軸目盛を調整
plt.ylim(0, 0.45) # y軸目盛範囲
plt.xticks(color="None") # x軸ラベルを消去
plt.yticks(color="None") # y軸ラベルを消去

plt.show()

# 所与の確率分布を仮定（2σ範囲）

# 所与の期待値と分散
mu = 0
variance = 1

# 期待値と分散(標準偏差)をもとに確率密度関数を生成
data_2 = np.linspace(mu-4, mu+4, 100)
sigma = np.sqrt(variance)
norm_pdf = stats.norm.pdf(x = data_2, loc = mu, scale = sigma)

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower_1 = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) # 確率変数μ-σ
upper_1 = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) # 確率変数μ+σ
lower_2 = stats.norm.pdf(x=mu-2*sigma, loc=mu, scale=sigma) # 確率変数μ-2σ
upper_2 = stats.norm.pdf(x=mu+2*sigma, loc=mu, scale=sigma) # 確率変数μ+2σ
lower_3 = stats.norm.pdf(x=mu-3*sigma, loc=mu, scale=sigma) # 確率変数μ-3σ
upper_3 = stats.norm.pdf(x=mu+3*sigma, loc=mu, scale=sigma) # 確率変数μ+3σ

# 確率密度関数のグラフを描画
plt.plot(data_2, norm_pdf, color = "tab:cyan", lw = 4)

# 垂直線
plt.vlines(x=mu, ymin=0, ymax=norm_pdf_max, color="orange", lw=1.5) # μ
plt.vlines(mu-sigma, 0, lower_1, color="black", lw=1, linestyle=':') # μ-σ
plt.vlines(mu+sigma, 0, upper_1, color="black", lw=1, linestyle=':') # μ+σ
plt.vlines(mu-2*sigma, 0, lower_2, color="black", lw=0.8,) # μ-2σ
plt.vlines(mu+2*sigma, 0, upper_2, color="black", lw=0.8) # μ+2σ
plt.vlines(mu-3*sigma, 0, lower_3, color="black", lw=1, linestyle=':') # μ-3σ
plt.vlines(mu+3*sigma, 0, upper_3, color="black", lw=1, linestyle=':') # μ+3σ

# テキストを配置
plt.text(mu-0.2, -0.03, 'μ', fontsize = 13, color = "darkorange") # μ
plt.text(mu-sigma-0.4, -0.03, 'μ-σ', fontsize = 10) # μ-σ
plt.text(mu+sigma-0.4, -0.03, 'μ+σ', fontsize = 10) # μ+σ
plt.text(mu-2*sigma-0.4, -0.03, 'μ-2σ', fontsize = 12) # μ-2σ
plt.text(mu+2*sigma-0.4, -0.03, 'μ+2σ', fontsize = 12) # μ+2σ
plt.text(mu-3*sigma-0.4, -0.03, 'μ-3σ', fontsize = 10) # μ-3σ
plt.text(mu+3*sigma-0.4, -0.03, 'μ+3σ', fontsize = 10) # μ+3σ
plt.text(mu-0.5, 0.16, '95.5%', fontsize = 14) # 95.5%

# 軸目盛を調整
plt.ylim(0, 0.45) # y軸目盛範囲
plt.xticks(color="None") # x軸ラベルを消去
plt.yticks(color="None") # y軸ラベルを消去

plt.show()

# 所与の確率分布を仮定（3σ範囲）

# 所与の期待値と分散
mu = 0
variance = 1

# 期待値と分散(標準偏差)をもとに確率密度関数を生成
data_2 = np.linspace(mu-4, mu+4, 100)
sigma = np.sqrt(variance)
norm_pdf = stats.norm.pdf(x = data_2, loc = mu, scale = sigma)

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower_1 = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) # 確率変数μ-σ
upper_1 = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) # 確率変数μ+σ
lower_2 = stats.norm.pdf(x=mu-2*sigma, loc=mu, scale=sigma) # 確率変数μ-2σ
upper_2 = stats.norm.pdf(x=mu+2*sigma, loc=mu, scale=sigma) # 確率変数μ+2σ
lower_3 = stats.norm.pdf(x=mu-3*sigma, loc=mu, scale=sigma) # 確率変数μ-3σ
upper_3 = stats.norm.pdf(x=mu+3*sigma, loc=mu, scale=sigma) # 確率変数μ+3σ

# 確率密度関数のグラフを描画
plt.plot(data_2, norm_pdf, color = "tab:cyan", lw = 4)

# 垂直線
plt.vlines(x=mu, ymin=0, ymax=norm_pdf_max, color="orange", lw=1.5) # μ
plt.vlines(mu-sigma, 0, lower_1, color="black", lw=1, linestyle=':') # μ-σ
plt.vlines(mu+sigma, 0, upper_1, color="black", lw=1, linestyle=':') # μ+σ
plt.vlines(mu-2*sigma, 0, lower_2, color="black", lw=1, linestyle=':') # μ-2σ
plt.vlines(mu+2*sigma, 0, upper_2, color="black", lw=1, linestyle=':') # μ+2σ
plt.vlines(mu-3*sigma, 0, lower_3, color="black", lw=0.8) # μ-3σ
plt.vlines(mu+3*sigma, 0, upper_3, color="black", lw=0.8) # μ+3σ

# テキストを配置
plt.text(mu-0.2, -0.03, 'μ', fontsize = 13, color = "darkorange") # μ
plt.text(mu-sigma-0.4, -0.03, 'μ-σ', fontsize = 10) # μ-σ
plt.text(mu+sigma-0.4, -0.03, 'μ+σ', fontsize = 10) # μ+σ
plt.text(mu-2*sigma-0.4, -0.03, 'μ-2σ', fontsize = 10) # μ-2σ
plt.text(mu+2*sigma-0.4, -0.03, 'μ+2σ', fontsize = 10) # μ+2σ
plt.text(mu-3*sigma-0.4, -0.03, 'μ-3σ', fontsize = 12) # μ-3σ
plt.text(mu+3*sigma-0.4, -0.03, 'μ+3σ', fontsize = 12) # μ+3σ
plt.text(mu-0.5, 0.16, '99.7%', fontsize = 14) # 99.7%

# 軸目盛を調整
plt.ylim(0, 0.45) # y軸目盛範囲
plt.xticks(color="None") # x軸ラベルを消去
plt.yticks(color="None") # y軸ラベルを消去

plt.show()
3
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
4