3. Pythonによる自然言語処理 3-1. 重要語抽出ツール TF-IDF分析［原定義］

• 自然言語処理を行うとき、具体的な狙いの一つとして「ある文章を特徴づけるような重要語を抽出したい」ということがあります。
• 単語を抽出するとき、まずはテキスト内で出現回数の多い単語を拾います。出現頻度順のリストの上位に挙がってくるのは、あらゆる文章に共通して頻繁に使われる語ばかりです。
• 品詞情報を使って名詞に限定しても、例えば「事」や「時」などのように特定の意味をなさない汎用的な単語が上位に多数出てくるので、それらをストップワードとして除外するなどの処理が必要です。

⑴ TF-IDFという考え方

• TF-IDF（Term Frequency - Inverse Document Frequency）、直訳すると「用語頻度 - 逆文書頻度」です。
• 出現回数は多いが、その語が出てくる文書の数が少ない、つまりどこにでも出てくるわけではない単語を特徴的で重要な語であると判定する考え方です。
• 多くは単語を対象とするものですが、文字や句（フレーズ）にも適用できますし、文書（ドキュメント）の単位もいろいろ応用がききます。

⑵ TF-IDF値の定義

出現頻度 $tf$ に、希少性の指標となる係数 $idf$ を掛け算する

• $tfidf=tf×idf$
• $tf_{ij}$ (単語$i$の文書$j$における出現頻度) × $idf_{i}$(単語$i$を含む文書の数の逆数の$log$)

出現頻度 $tf$ と係数 $idf$ はそれぞれ次のように定義されます

• $tf_{ij}=\dfrac{n_{ij}}{\sum_{k}n_{kj}} = \dfrac{単語iの文書jにおける出現回数}{文書jにおける全ての単語の出現回数の和}$
• $idf_{i}=\log \dfrac{|D|}{|{d:d∋t_{i}}|} = \log{\dfrac{全文書の数}{単語iを含む文書の数}}$

⑶ 原定義による計算のしくみ

# 数値計算ライブラリのインポート
from math import log
import pandas as pd
import numpy as np

➀ 単語データリストを用意

• すでに形態素解析などの前処理を済ませて、6つの文書について次のような単語のリストができているという想定で、対象となる3つの単語の$tfidf$を計算します。

docs = [
        ["語1", "語3", "語1", "語3", "語1"],
        ["語1", "語1"],
        ["語1", "語1", "語1"],
        ["語1", "語1", "語1", "語1"],
        ["語1", "語1", "語2", "語2", "語1"],
        ["語1", "語3", "語1", "語1"]
        ]

N = len(docs)

words = list(set(w for doc in docs for w in doc))
words.sort()

print("文書数：", N)
print("対象となる単語：", words)

➁ 計算用の関数を定義

• あらかじめ出現頻度 $tf$、係数 $idf$、それらを掛け合わせた $tfidf$ をそれぞれ計算する関数を定義します。

# 関数tfの定義
def tf(t, d):
    return d.count(t)/len(d)

# 関数idfの定義
def idf(t):
    df = 0
    for doc in docs:
        df += t in doc
    return np.log10(N/df)

# 関数tfidfの定義
def tfidf(t, d):
    return tf(t,d) * idf(t)

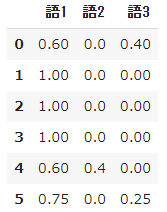
➂ TFの計算結果を観察

• 参考までに、段階的に $tf$ 及び $idf$ の計算結果をみておきましょう。

# tfを計算
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]     
        temp.append(tf(t,d))
    result.append(temp)

pd.DataFrame(result, columns=words)

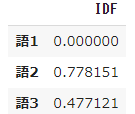
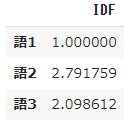
➃ IDFの計算結果を観察

# idfを計算
result = []
for j in range(len(words)):
    t = words[j]
    result.append(idf(t))

pd.DataFrame(result, index=words, columns=["IDF"])

• 6つの文書すべてに出てくる語1の係数 $idf$ は 0 となり、また1つの文書にしか出てこない語2は最も大きく0.778151 となっています。

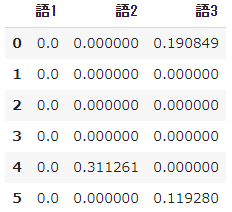
➄ TF-IDFの計算

# tfidfを計算
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]
        temp.append(tfidf(t,d))   
    result.append(temp)

pd.DataFrame(result, columns=words)

• 語1の $tfidf$ は、係数 $idf$ が 0 なので 、たとえ出現回数がどんなに多くても一律 0 になってしまいます。
• また、TF-IDFはそもそも情報検索の目的で提案された指標であり、1回も出現しない語に対しては $idf$ を計算する上で分母が 0（いわゆるゼロ除算）となってエラーになってしまいます。

⑷ scikit-learnによる計算

• そうした問題点に対応して scikit-learn の TF-IDF ライブラリTfidfVectorizerは、原定義とはやや異なる定義で実装されています。

# scikit-learnのTF-IDFライブラリをインポート
from sklearn.feature_extraction.text import TfidfVectorizer

• 先の6つの文書の単語データリストを対象にTfidfVectorizerをつかって $tfidf$ を計算してみます。

# 1次元のリスト
docs = [
        "語1 語3 語1 語3 語1",
        "語1 語1",
        "語1 語1 語1",
        "語1 語1 語1 語1",
        "語1 語1 語2 語2 語1",
        "語1 語3 語1 語1"
        ]

# モデルを生成
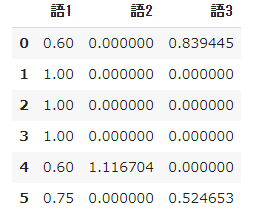
vectorizer = TfidfVectorizer(smooth_idf=False)
X = vectorizer.fit_transform(docs)

# データフレームに表現
values = X.toarray()
feature_names = vectorizer.get_feature_names()
pd.DataFrame(values,
             columns = feature_names)

• 語1の $tfidf$ は各文書で 0 ではなくなり、また語2、語3においては元から 0 であった文書を除いて原定義とは異なる値になっています。
• そこで、原定義に基づいて scikit-learn の結果を再現してみます。

⑸ scikit-learnの結果を再現

➀ IDFの計算式を変更

# 関数idfの定義
def idf(t):
    df = 0
    for doc in docs:
        df += t in doc
    #return np.log10(N/df)
    return np.log(N/df)+1

• np.log10(N/df)をnp.log(N/df)+1に修正
• つまり底を10とする常用対数から、底をネイピア数eとする自然対数に変えて、さらに+1します。

# idfを計算
result = []
for j in range(len(words)):
    t = words[j]
    result.append(idf(t))

pd.DataFrame(result, index=words, columns=["IDF"])

➁ TF-IDFの計算結果を観察

# tfidfを計算
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]
        temp.append(tfidf(t,d))   
    result.append(temp)

pd.DataFrame(result, columns=words)

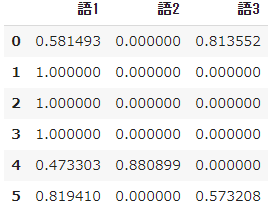
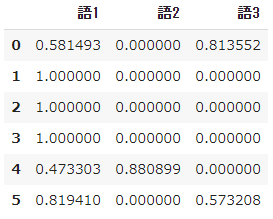
➂ TF-IDF計算結果をL2正則化

• 最後に $tfidf$ の計算結果をL2正則化します。
• つまり値をスケーリングして、それらがすべて2乗されて合計すると1になるように変換します。
• なぜ正則化が必要かといえば、各単語が各文書に出現する回数を数えているわけですが、各文書は長さが異なりますので、文書が長いほど単語の数は多くなりがちです。
• そうした単語の合計数による影響を取り除くことによって、単語の出現頻度を相対的に比較することが可能となります。

# 試しに文書1のみ定義に従ってノルム値を計算
x = np.array([0.60, 0.000000, 0.839445])
x_norm = sum(x**2)**0.5
x_norm = x/x_norm
print(x_norm)

# それらを2乗して合計し、1になることを確認
np.sum(x_norm**2)

• ここは scikit-learn を利用して楽をしましょう。

# scikit-learnの正則化ライブラリをインポート
from sklearn.preprocessing import normalize

# L2正則化
result_norm = normalize(result, norm='l2')

# データフレームに表現
pd.DataFrame(result_norm, columns=words)

• 整理しておくと、scikit-learn の TF-IDF は、原定義のもつ2つの難点を解消するものとなっています。
• 係数 $idf$ の計算式に自然対数を用い、かつ+1することによってゼロを回避する。ちなみに常用対数から自然対数への変換は約 2.303 倍になります。
• さらにL2正則化によって、文書ごとの長短に伴う単語数の差の影響が排除されています。
• TF-IDF の原理はとてもシンプルなものですが、scikit-learn にはパラメータもいろいろありますし、課題によってチューニングしていく余地もありそうです。
• 3. Pythonによる自然言語処理　3-2. TF-IDF分析［小説にみる特徴語の検出］