- リッジ回帰・ラッソ回帰それぞれの正則化の効き方の違いを、もう少し詳しく見ていきたいと思います。
- 正則化パラメータ$λ$を50通り生成して、それぞれの回帰モデルについて$λ$を入れ替えながら推定を50回くり返します。
- その過程で、変数ごとに推定される係数がどのように変化していくかを観察します。
⑴ ライブラリのインポート
# データ加工・計算・分析ライブラリ
import numpy as np
import pandas as pd
# グラフ描画ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline
# 機械学習ライブラリ
import sklearn
from sklearn.linear_model import Ridge, Lasso # 回帰モデル生成のためのクラス
# matplotlibを日本語表示に対応させるモジュール
!pip install japanize-matplotlib
import japanize_matplotlib
⑵ データの取得と読み込み
# データを取得
url = 'https://raw.githubusercontent.com/yumi-ito/sample_data/master/ridge_lasso_50variables.csv'
# 取得したデータをDataFrameオブジェクトとして読み込み
df = pd.read_csv(url)
print(df)
- このダミーデータは、列の0番目が目的変数y、列の1番目以降の説明変数は全部で50あります。標本数は150です。
- すでに標準化をしてあるので、各変数はいずれも平均0、標準偏差1となっています。
- また、目的変数yですが、これは意図的に作成されています。1番目の変数x_1の正しい係数を「5」とし、これに正規分布に従うノイズを加算して算出されたものです。その正解「5」を推定できるかどうかも一つの関心となります。
# 「y」列を削除して説明変数xを作成
x = df.drop('y', axis=1)
# 「y」列を抽出して目的変数yを作成
y = df['y']
⑶ 正則化パラメータλの生成
# λ(alpha)を50通り生成
num_alphas = 50
alphas = np.logspace(-2, 0.7, num_alphas)
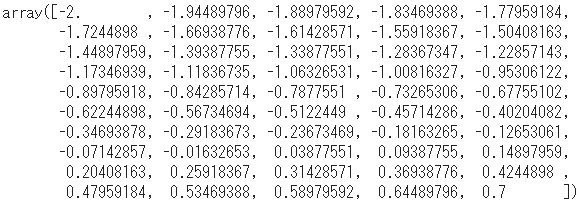
print(alphas)
-
numpy.logspace()は、底を10とする対数をとると等差数列になるという、ひとひねりのある関数です。 - 引数に
(開始値, 終了値, 生成する数)を指定しますが、実際に対数をとってみると次のようになります。
np.log10(alphas)
- 開始値-2、終了値0.7、全50個の等差数列になっています。
- 等差数列なら
numpy.arange()でも良さそうなところを、あとで可視化する際に対数目盛をつかう必要からこのようにしています。
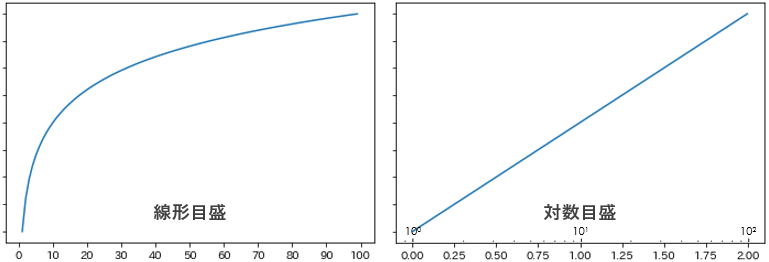
対数目盛
-
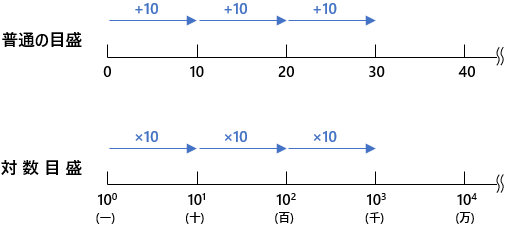
対数目盛は、目盛ごとに値が倍々に増えていきます。x軸かy軸のいずれか、もしくは両方の軸につかったものを対数グラフといいます。
-
普通の目盛のことを線形目盛と呼びますが、それを対数目盛に変換すると・・・
-
数直線上でギュッと軸目盛を圧縮したような感じになるので、桁数のかけ離れたデータなどを視覚的に比較しやすくしてくれます。
⑷ リッジ回帰による推定
# 回帰係数を格納する変数
ridge_coefs = []
# alphaを入れ替えながらリッジ回帰の推定をくりかえす
for a in alphas:
ridge = Ridge(alpha = a, fit_intercept = False)
ridge.fit(x, y)
ridge_coefs.append(ridge.coef_)
-
alphaを入れ替えながらリッジ回帰の推定をくりかえし、回帰係数をridge_coefsに追加していきます。 - モデルのひな型を生成する
Ridge()の引数fit_intercept = Falseは、切片を計算するかどうかという指定で、Falseにすると切片を計算しない、すなわち切片0で必ず原点を通ることになります。
# 集積された回帰係数をnumpyのarrayに変換
ridge_coefs = np.array(ridge_coefs)
print("配列の形状:", ridge_coefs.shape)
print(ridge_coefs)
- 50×50の配列で、パラメータ毎に50通り、係数50個の組が得られています。
- これを可視化します。x軸にパラメータを置きますが、
alphasを対数変換してマイナスをかけたlog_alphasをつかいます。 - グラフ内にテキスト表示をする
plt.text()関数は、引数は(x, y, "str")で座標と文字列を指定します。
# alphasを対数変換(-log10)
log_alphas = -np.log10(alphas)
# グラフ領域のサイズ指定
plt.figure(figsize = (8,6))
# x軸にλ、y軸に係数を置いた折れ線グラフ
plt.plot(log_alphas, ridge_coefs)
# 説明変数x_1を表示
plt.text(max(log_alphas) + 0.1, np.array(ridge_coefs)[0,0], "x_1", fontsize=13)
# x軸の範囲を指定
plt.xlim([min(log_alphas) - 0.1, max(log_alphas) + 0.3])
# 軸ラベル
plt.xlabel("正則化パラメータλ(-log10)", fontsize=13)
plt.ylabel("回帰係数", fontsize=13)
# 目盛線
plt.grid()
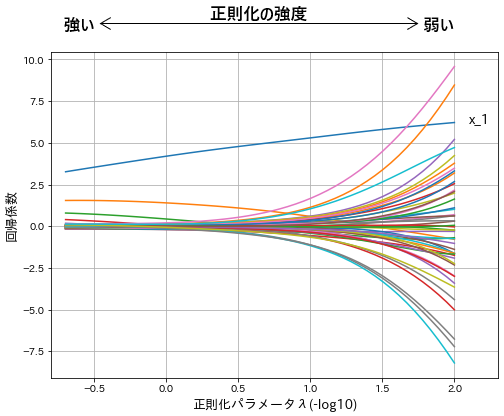
- x軸が$-log_{10}$なので、左へ行くほど正則化パラメータ$λ$の値は大きく、ペナルティの強度は強くなります。
- 説明変数x_1をもとに目的変数yを生成しているので、変数x_1だけは独り線形を示しています。
- 左側に行くほど係数の絶対値は小さく、右側へ行くほどペナルティの縛りが緩くなるので絶対値の大きい係数が推定されやすいという傾向が見てとれます。
⑸ ラッソ回帰による推定
- リッジ回帰と同じ正則化パラメータ(alphas)をつかって、ラッソ回帰の推定を50回くり返します。
# 回帰係数を格納する変数
lasso_coefs = []
# alphaを入れ替えながらラッソ回帰の推定をくりかえす
for a in alphas:
lasso = Lasso(alpha = a, fit_intercept = False)
lasso.fit(x, y)
lasso_coefs.append(lasso.coef_)
# 集積された回帰係数をnumpyのarrayに変換
lasso_coefs = np.array(lasso_coefs)
print("配列の形状:", lasso_coefs.shape)
print(lasso_coefs)
- 同じくx軸が$-log_{10}$の片対数グラフを描画します。
# グラフ領域のサイズ指定
plt.figure(figsize = (8,6))
# x軸にλ、y軸に係数を置いた折れ線グラフ
plt.plot(log_alphas, lasso_coefs)
# 説明変数x_1を表示
plt.text(max(log_alphas) + 0.1, np.array(lasso_coefs)[0,0], "x_1", fontsize=13)
# x軸の範囲を指定
plt.xlim([min(log_alphas) - 0.1, max(log_alphas) + 0.3])
# 軸ラベル
plt.xlabel("正則化パラメータλ(-log10)", fontsize=13)
plt.ylabel("回帰係数", fontsize=13)
# 目盛線
plt.grid()
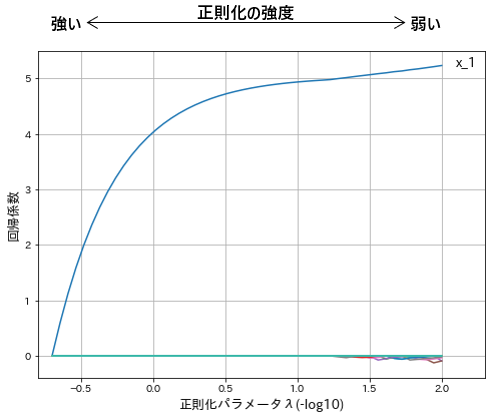
- 変数x_1以外は、係数がほぼ0となっています。
- それ以外の変数で、0ではない係数は、右端の方のパラメータの強度がもっとも緩いあたりにわずかに見られます。
まとめ
- リッジ回帰は、数ある変数に対して`全体的に絶対値の小さい係数が推定される傾向があります。
- ラッソ回帰は、部分的に少数の変数は0ではない係数となり、それ以外の係数はすべて0になるという傾向があります。
- ラッソ回帰では係数のほとんどが0になることから、回帰係数を求めながら同時に次元削減をしているに等しいともいえましょう。