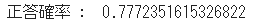4. Pythonで考えるベイズ統計 1-1. ナイーブベイズによる感情判定［ベイズの定理］

• ここしばらく感情分析を扱ってきましたが、いずれも「感情値辞書」にもとづく方法でした。一方、機械学習をつかった感情値判定も盛んに行われています。
• その中でも論理が単純明快で、かつ実用性も認められている**ナイーブベイズフィルタ（単純ベイズ分類器）**を取り上げます。 Python で自然言語処理プログラムを構築するための主要なプラットフォーム NLTK（Natural Language Toolkit） でも提供されていて簡単に行うことができます。

#⑴ ベイズ統計の基礎知識

###１. ベイズ統計学小史

• ベイズという名称は、18世紀の英国を生きた牧師トーマス・ベイズ（Thomas Bayes, 1702-1761）の名前です。彼が趣味で数学の研究をしていた際に、いわゆる**「ベイズの定理」**を発見したのは1740年代とされています。その後、フランスの数学者 ピエール＝シモン・ラプラス（Pierre=Simon Laplace, 1749-1827）が独自にこれを再発見し、客観的な数式に定義してその実用性を示しました。
• しかし、ラプラス自身がやがて疑問を持ち、その後200年以上使われなかっただけでなく、20世紀においては特にタブー視されて、統計学の教科書には申し訳程度に説明があるばかりの存在でした。統計学は伝統的に客観的な確率に拠って立つもので、これに反して主観的な確率に基づくベイズ統計学は到底受け入れられるものではありませんでした。
• 個人的な経験になりますが、 筆者がベイズ統計学の指導をうけた先生の発言がとても印象に残っています。「ベイズ の "不幸" は AI とか機械学習という言葉の方がイメージだけで先行してしまったことだ。」 要するに、近年急速に普及した AI や機械学習の基礎にあるのがベイズ統計学です。

###２. ベイズの定理（Bayes' theorem）

• 確率に関する「ベイズの定理」の公式を示します。
  

• では、例題で具体的に考えていきます。
  
  さて、検査Bをうけて陽性となった場合、実際に病気Aにかかっている確率は何%でしょうか。
  

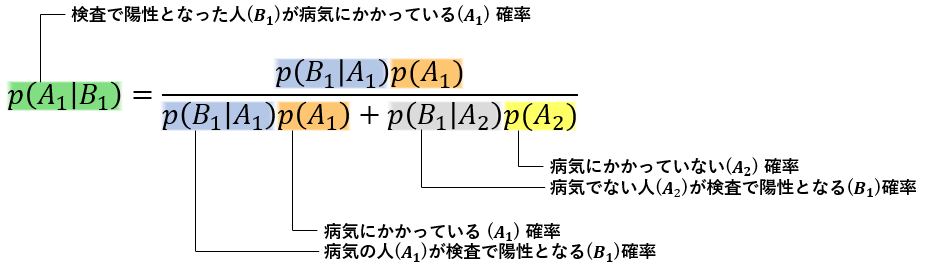
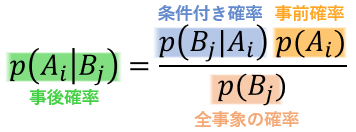
• 上式は「ベイズの定理」にあてはめたもので、[$A_1$ : 罹患者, $A_2$ : 非罹患者]　[$B_1$ : 陽性, $B_2$ : 陰性] としていますが、具体的な数値を代入して計算してみます。
  

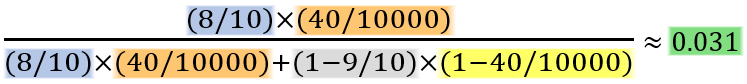
• 陽性という判定をうけたとしても、実際に病気にかかっている確率は 3 %ほどで、100 人中およそ 97 人は病気ではありません。
  

• 計算の前提となる「事前確率」に主観確率が利用されるため、ベイズ統計学は長い間タブー視されましたが、一方このような使用法に限っては認められていました。いわば「ベイズの定理」の正しい使い方です。

• この例では「事前確率」である罹患率も、罹患者の検査陽性率もデータに基づいて計算された頻度に基づく客観確率です。要するに、事前確率に客観確率を利用するのであれば、今も昔も「ベイズの定理」が正しいことに変わりはありません。

• 主観確率とは、何らかの事象が発生する確度を個人的な信念にもとづいて 0～1 の数値で表現したものです。例えば、サイコロを投げて 1 の目が出る確率が 1/2 であると個人が想定した場合、それがその人にとっての主観確率といえます。そのサイコロをくり返し投げてみて、それぞれの目が出る頻度が 1/6 であった場合、それぞれの目が出る確率は客観的に 1/6 と推定されます。

###３. ベイズ更新（Bayesian updating）

• 例題で具体的に見ていきます。
  

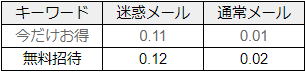
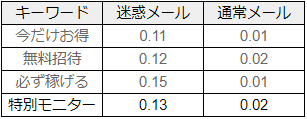
• 同じくデータベースから「今だけお得」という言葉が迷惑メールと通常メールそれぞれに含まれる確率を調べた結果が以下となります。
  
  

• あるメール X が迷惑メールである確率は約 94 %ですが、通常メールである確率も約 6 %ありますから、迷惑メールとして削除するにはまだ危険性があります。

• そこで、この事後確率を、今度は事前確率として利用して新たに「無料招待」という言葉について「ベイズの定理」を適用します。
  
  

• さらに事前確率を更新し、データを追加して「必ず稼げる」という言葉について「ベイズの定理」を適用します。
  
  

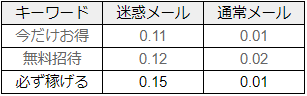
• 同じように、今度は「特別モニター」という言葉について「ベイズの定理」を適用すると、次のように事後確率は限りなく 100 %に近づきます。
  
  

• このように次々と「ベイズの定理」を適用することをベイズ更新といいます。たった 4 回ベイズ更新をしただけで、あるメール X が迷惑メールでない可能性は約 0.0001 %になりました。

• 特徴にもとづいて事後確率を求めるのがベイズ流の考え方ですが、厳密には特徴のそれぞれが互いに独立でなければいけません。例えば「特別モニター」や「無料招待」は互いに影響していると考えられますが、そうした点に目を瞑っても実用上大いに有効であることが知られています。

• 要するに、文中の単語はすべて独立であると仮定して単純化された方法論であり、それが「**ナイーブ（=単純な）**ベイズ・フィルタ」と呼ばれる所以です。

###４. データ増加による事後確率の安定化

• 「ベイズの定理」によって計算される事後確率は、事前確率によって大きく変動します。そもそも「ベイズの定理」が長らく爪弾きされてきたのも、主観的かつ恣意的な事前確率によって、事後確率はどのような値にでもなってしまうからでした。

• ここに「客観的なデータをたくさん集めれば、事前確率の影響が小さくなり、事後確率は安定するのではないか」という考え方が出てきました。データの量と質によって、事前確率の影響力を事実上なくしてしまえばよい、という主張です。

• かりに、全メールにおける迷惑メールの割合は、確かにデータベースから調べることはできますが、実際さまざまな制約があって調べることが出来ないとすれば、主観的な印象から事前確率を恣意的に決めざるを得ません。そこで再び迷惑メール問題です。
  

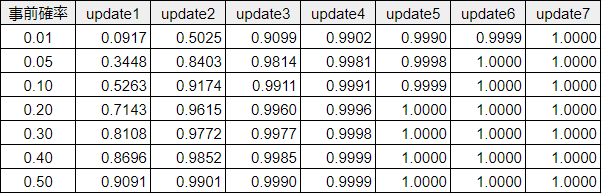
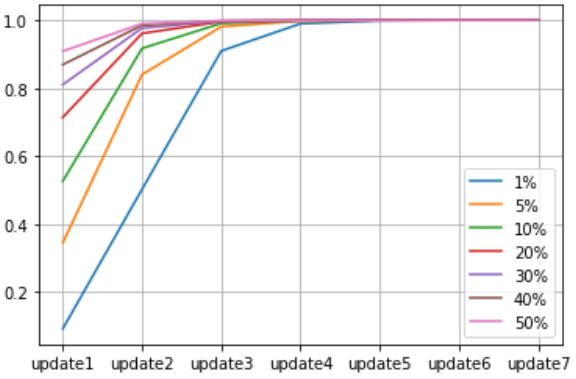
• 下表は、事前確率が「100通あたり1通 (0.01)」から「全メールの半分 (0.50)」まで 7 通りあるとして、それぞれについてベイズ更新をくり返して事後確率の変化をまとめたものです。
  

• 事前確率が 0.01 でも 0.50 であっても、4 回目の更新で事後確率は 99 %を超えています。データの量が物を言う、とばかりに客観的なデータの増加が事後確率を安定化させることがわかります。
  

#⑵ データセットの概要

• 米国の最難関大学として知られるコーネル大学で、感情分析のために実施された映画レビューのデータを利用します。公式サイト : Movie Review Data
• 人手によってポジティブ/ネガティブに分類されたコメント文が、各 5,331 文ずつ収録されています。
• 右のリンクから自動的にダウンロードできます。http://www.cs.cornell.edu/people/pabo/movie-review-data/rt-polaritydata.tar.gz

#⑶ データセットの取り込み

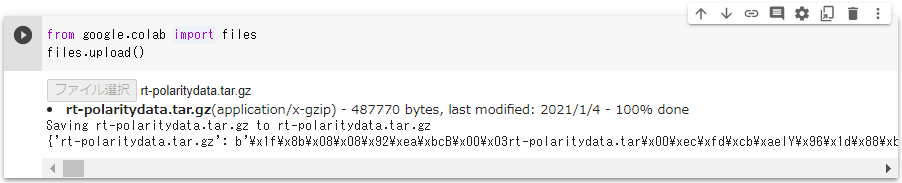
• ローカルPCにダウンロードされた圧縮ファイル rt-polaritydata.tar.gz を Colaboratory 上にアップロードします。

from google.colab import files
files.upload()

• ファイルの拡張子は .tar.gz で、これは複数のファイルを tar コマンドで一つにアーカイブしたファイルが gzip コマンドで圧縮されている状態なので !tar -zxvf で解凍・展開します。

!tar -zxvf rt-polaritydata.tar.gz

• 展開されたファイルは全部で 3 つ、README ファイルはさておき、残る 2 ファイルの末尾 .neg と .pos がそれぞれネガティブとポジティブに分類されたデータ群となっています。

#⑷ データの前処理

###１. NLTK のインポート

import nltk
from nltk.tokenize import word_tokenize
nltk.download('punkt')

• NLTK パッケージ、及び文章をトークンに分割するトークナイザをインポートします。トークンとは、それで一つの意味をもち、それ以上細かくすると意味を持たない最小単位の "まとまり" のことです。
• ちなみに、word_tokenize はその名のとおり単語のトークン化を行ないますが、その前に実行される punkt は文のトークナイザです。

###２. データの前処理を行うメソッドを定義

def format_sentense(sentense):
    return {word: True for word in word_tokenize(sentense) }

• 内包の外側の { } で dict 型を指定し、word_tokenize() によりトークン毎に、その単語をキーとし、値はブール値 True として返します。

###３. データの前処理

# ポジティブなデータの前処理
pos_data = []
with open('rt-polaritydata/rt-polarity.pos', encoding='latin-1') as f:
    for line in f:
        pos_data.append([format_sentense(line), 'pos'])

# ネガティブなデータの前処理
neg_data = []
with open('rt-polaritydata/rt-polarity.neg', encoding='latin-1') as f:
    for line in f:
        neg_data.append([format_sentense(line), 'neg'])

• 例として、ポジティブに分類された最初のコメント文を示します。
  

• こちらが前処理されると次ようになります。
  

###４. 訓練用データと検証用データに分割

• ポジティブとネガティブそれぞれ 4,000 文ずつを合わせた計 8,000 文を訓練データとしてモデルを生成し、また残りのポジネガ 1,331 文ずつを合わせた計 2,662 文をつかってモデルの精度を評価します。

# 訓練データの取得
training_data = pos_data[:4000] + neg_data[:4000]

# 評価データの取得
testing_data = pos_data[4000:] + neg_data[4000:]

#⑸ 訓練データによるモデル生成

###１. モデルの生成

• NLTK の NaiveBayesClassifier クラスを利用して、訓練データにもとづいてモデルを生成します。

from nltk.classify import NaiveBayesClassifier

# モデルの生成
model = NaiveBayesClassifier.train(training_data)

###２. モデルの試行

• 試しに 2 つの例文をつかって、モデルがどのように判定するかを見てみます。
  

es1 = "This is a hilarious movie and I would watch it again and again."
es2 = "This is a boring movie and once you see it, you'll have enough."

# 判定結果を出力
print( es1, '--->', model.classify(format_sentense(es1)) )
print( es2, '--->', model.classify(format_sentense(es2)) )

#⑹ テストデータによるモデルの精度評価

• 関数 accuracy() は、第二引数に指定されたテストデータにおけるモデルの精度を計算します。
• 具体的には、モデルが正しくラベル付けしたパーセンテージを測定します。例えば、テストデータが 80 個あったとして、そのうち正しい予測を 60 回するモデルは 75 %の精度をもっています。

from nltk.classify.util import accuracy

print('正答確率 : ', accuracy(model, testing_data))

• 先の例文に対する判定結果も良好ですし、またモデルとして 8 割弱の精度があると評価されています。