TL;DR
アドベントカレンダーの記事が決まっていなかったので、興味のあった機械学習をこの機会に学習してみました。ちなみに普段はPHPプログラマーとしてWeb系のシステムを開発しています。
ニューラルネットワーク(Neural Network)とは?
ニューラルネットワークはニューロン(脳の神経細胞)が情報を伝達する仕組みを模倣して作られたアルゴリズムで、機械学習で広く利用されています。人工的に作られたという意味でArtificial Neural Network(ANN)なんて呼ばれたりもしています。
ニューラルネットワークの層が深いとディープラーニングと呼ばれるらしいですが、その定義は時代によって変化しているようで、以前は隠れ層が10層くらいあればディープラーニングと呼ばれたようですが、現在は100層以上の隠れ層を持っているニューラルネットワークをディープラーニングと呼ぶそうです。
単層ニューラルネットワーク
本当は多層ニューラルネットワークを試したかったですが、約一週間の詰め込み学習では間に合いませんでした。という事で今回は単層ニューラルネットワークを作りながら機械学習の基礎を学んでいきます。
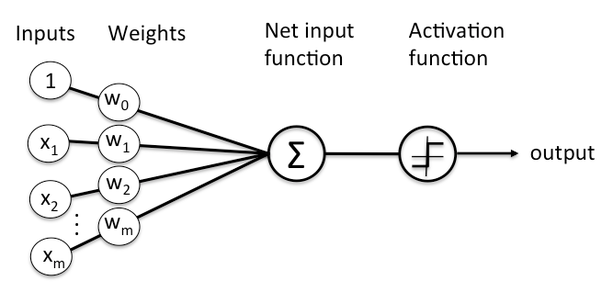
以下の図は単層ネットワークのイメージです。
重みと掛け合わされた4つの入力の総和を活性化関数(この図ではステップ関数)に渡して結果を出力としています。
この入力から出力までの流れを順伝播と呼ぶそうです。今回はforwardメソッドとして実装します。
ニューラルネットワークのクラスを作る
メソッドの中身はとりあえず全部空にしています。
import numpy as np
class NN():
def __init__(self):
def sigmoid(self, x):
def sigmoid_derivative(self, x):
def train(self, target_inputs, target_output):
def forward(self, inputs):
重みと学習率を設定する
初期化メソッドでクラスのプロパティの重みの初期値と学習率をセットします。学習前に設定するこれらの値はハイパーパラメータなんて呼ばれています。
後ほど実装するtrainメソッドで、重みの値を更新して期待する値に出力が近づくように調整して学習させていきます。
学習率の値が大きいとより速く学習させることが可能ですが、大きくし過ぎると期待値を通りすぎて行ったり来たりして収束しなくなってしまうことがあります。また学習率は1以下に設定するのが一般的なようです。
ということで今回は0.25にしてみました。
def __init__(self):
self.w = np.array([1, 2, 3, 4])
self.lr = 0.25
活性化関数(Activation Function)
今回は活性化関数にシグモイド関数を使うので、メソッドとして準備しておきます。
def sigmoid(self, x):
y = 1 / (1 + np.exp(-x))
return y
この数式をそのままコードに書いています。
$$y(x)=\frac{1}{1+e^{-x}}$$
シグモイド関数は0から1の間で滑らかな曲線を描く関数の為、このニューラルネットワークの出力は0から1の間の数字になります。したがって目標値を1より大きい値にしてしまうと上手く動作しません。
順伝播(Forward Propagation)
入力と重みを掛け合わせた総和を、シグモイド関数に渡して出力するだけのメソッドです。
def forward(self, inputs):
output = self.sigmoid(np.dot(inputs, self.w))
return output
学習済みのニューラルネットワークに学習データを順伝播して出力を見ることで、学習効果を確認することができます。
学習メソッド
学習部分をtrainメソッドとして実装していきいます。
中身は以下のようになります。
def train(self, target_inputs, target_output):
# 学習データの入力と重みの行列積
hidden_outputs = np.dot(target_inputs, self.w)
# 活性化関数にhidden_outputsを渡して、final_output(0~1の値)を求める
final_output = self.sigmoid(hidden_outputs)
# 目標値と出力の誤差
output_error = target_output - final_output
# 重みの更新
delta_w = self.lr * output_error * self.sigmoid_derivative(hidden_outputs)
self.w = self.w + delta_w
引数のtarget_inputsとtarget_outputには以下のような学習データを想定しています。
# 学習の入力データ
target_inputs = np.array([0.2, -0.5, 0.1, 0.7])
# 目標値
target_outputs = np.array(0.777)
重み更新の部分では勾配降下法を使ってδwを求め、現在の重みに加算代入して更新しています。
シグモイド関数の導関数
trainメソッド内で重みを更新する際に勾配降下法を利用するため、シグモイド関数の導関数をメソッドとして定義していました。
def sigmoid_derivative(self, x):
y = 1 - self.sigmoid(x) * self.sigmoid(x)
return y
学習させてみる
さて、学習メソッドができたので、実際に学習させてみます。
目標値は0.777に設定しているので、学習の度に重みが調整され、出力がこの目標値に近づくかを確認してみます。
nn = NN()
target_inputs = np.array([0.2, -0.5, 0.1, 0.7])
target_outputs = np.array(0.777)
for iteration in range(1):
nn.train(target_inputs,target_outputs)
print(nn.forward(np.array([0.2, -0.5, 0.1, 0.7])))
一回だとこのような結果になりました!
0.942667947251
目標としている0.777からは程遠いですね。
今度は学習回数を100に設定して試してみます。(forループのrangeの値を変えています)
0.916580545292
まだダメですね。
では今度は1000回学習させてみます。
0.777005081215
かなり目標値に近づくことができました!
以下、完成版のコードになります。
import numpy as np
class NN():
def __init__(self):
self.w = np.array([1, 2, 3, 4])
self.lr = 0.25
def sigmoid(self, x):
y = 1 / (1 + np.exp(-x))
return y
def sigmoid_derivative(self, x):
y = 1 - self.sigmoid(x) * self.sigmoid(x)
return y
def train(self, target_inputs, target_output):
# 学習データの入力と重みの行列積
hidden_outputs = np.dot(target_inputs, self.w)
# 活性化関数にhidden_outputsを渡して、final_output(0~1の値)を求める
final_output = self.sigmoid(hidden_outputs)
# 目標値と出力の誤差
output_error = target_output - final_output
# 重みの更新
delta_w = self.lr * output_error * self.sigmoid_derivative(hidden_outputs)
self.w = self.w + delta_w
def forward(self, inputs):
output = self.sigmoid(np.dot(inputs, self.w))
return output
nn = NN()
target_inputs = np.array([0.2, -0.5, 0.1, 0.7])
target_outputs = np.array(0.777)
for iteration in range(1):
nn.train(target_inputs,target_outputs)
print(nn.forward(np.array([0.2, -0.5, 0.1, 0.7])))
まとめ
単層ニューラルネットワークを実装するのも中々大変でした。
フルスクラッチで多層ニューラルネットワークを作れるようになれば色々と世界が広がりそうなので、今後もチャレンジしていきたいです。
![]() FORK Advent Calendar 2018
FORK Advent Calendar 2018
![]() 11日目 Chromebookのコンソールでフォントを変更する @howking
11日目 Chromebookのコンソールでフォントを変更する @howking