本記事の目的

確率論において重要な定理である「中心極限定理」を Python で確かめます．
具体的には，「ある分布から取り出した標本平均の分布が，標本を大きくすることで本当に正規分布に従うのか？」を確かめます．

中心極限定理とは

数学的に厳密な内容は述べませんが，中心極限定理が何なのかをざっくりと述べます．

定理の内容（ざっくりと）
$n$ 個の確率変数 $X_1,\cdots ,X_n$ が独立で同じ分布に従うとする．
$E[X_i]=\mu, V[X_i]=\sigma^2, \bar{X}=\frac{1}{n}(X_1 + \cdots + X_n)$ とする．
このとき，$n$ を大きくすると，$\bar{X}$ は正規分布 $N(\mu, \sigma^2 /n)$ に近づく．
※ ここで，$n$ が標本の大きさ，$\bar{X}$ が標本平均です．

記事を書くに至った経緯
この定理の証明は確率統計の教科書に載っていますが，個人的には難しいと思いました．
そこで，「本当に $n$ を大きくして標本平均が正規分布に従うのか？」を Python で実験的に確かめようと思ったのが，この記事を書こうと思った経緯です．

本記事で確かめること

$X_i$ の分布として，以下の4つを取り扱います．

一様分布（連続型）
二項分布（離散型）
自作の確率分布（離散型）
コーシー分布（連続型）

それぞれの分布からの標本平均の分布を可視化し，正規分布っぽくなっているか確認します．
具体的には以下のような手順です：

標本の大きさ size を決める．
size 個の標本平均を求めることを一定数繰り返し，標本平均の分布を描画する．
対応する正規分布を一緒に描画して，確かめる．

この際の標本の大きさ size はいろいろ変えて実験します．
上の4つの分布のうち，コーシー分布だけは期待値や分散が存在しない分布です．
そのためコーシー分布から取ってきた標本平均は $n$ を大きくしても正規分布になりません（中心極限定理が成り立たない）．それについても確かめてみます．

一様分布

$X_1, \cdots, X_n$ が一様分布に従う場合を考えます．
具体的には，$X_i \sim U(0,10)$ とします．

以下にコードを載せます．

一様分布U(0,10)からの標本平均に対して中心極限定理を確かめる

fig = plt.figure(figsize=(20, 12), dpi=200)
# 標本の大きさのリスト
size_list = [1, 2, 10, 50, 100, 1000, 10000, 100000]
# 一様分布U(loc, loc+scale)のパラメータ
loc = 0
scale = 10

for _, size in enumerate(size_list):
  ax = fig.add_subplot(2, 4, i+1)
  plt.title(f'$size={size}$')

  # 一様分布からsize個サンプリングして標本平均を求めることを1000回繰り返す
  sm = np.ndarray(1000)
  for i in range(1000):
      vals = stats.uniform.rvs(loc=loc, scale=scale, size=size)
      sm[i] = np.mean(vals) # size個の平均を計算

  # 一様分布の平均と分散を計算
  mu = stats.uniform.mean(loc=loc, scale=scale)
  var = stats.uniform.var(loc=loc, scale=scale)

  # 一様分布の標本平均の分布をヒストグラムとして描画
  plt.hist(sm, alpha=0.4, label='sm', bins=20, density=True)
  # 正規分布のpdfを描画
  x = np.arange(mu-2.58*(var/size)**0.5, mu+2.58*(var/size)**0.5, 0.001) # 99%点まで描画
  norm_vals = stats.norm.pdf(x, loc=mu, scale=(var/size)**0.5) # pdfの値を生成
  plt.plot(x, norm_vals, label='norm')
  plt.legend()
# 余白を調整して保存
plt.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.95)
plt.savefig('uniform_clt.png')

コードの解説
scipy.stats.uniform の rvs() という関数を使うことで，一様分布からのサンプリングを行います．
サンプリングした後それらの平均を計算します．
これを繰り返す（プログラム中では1000回）ことで，一様分布から取り出した標本平均のヒストグラムを描画します．これで標本平均の分布が大体わかるという感じです．
そのヒストグラムと，正規分布 $N(\mu, \sigma^2 /n)$ の確率密度関数を重ねてプロットします．
今回は一様分布なので $\mu=(0+10)/2=5,~~\sigma^2=(10-0)^2/12=\frac{100}{12}=\frac{25}{3}$ です．
$n$ は標本の大きさで，今回は [1, 2, 10, 50, 100, 1000, 10000, 100000] の8パターンを試します．
その結果が以下の画像です．

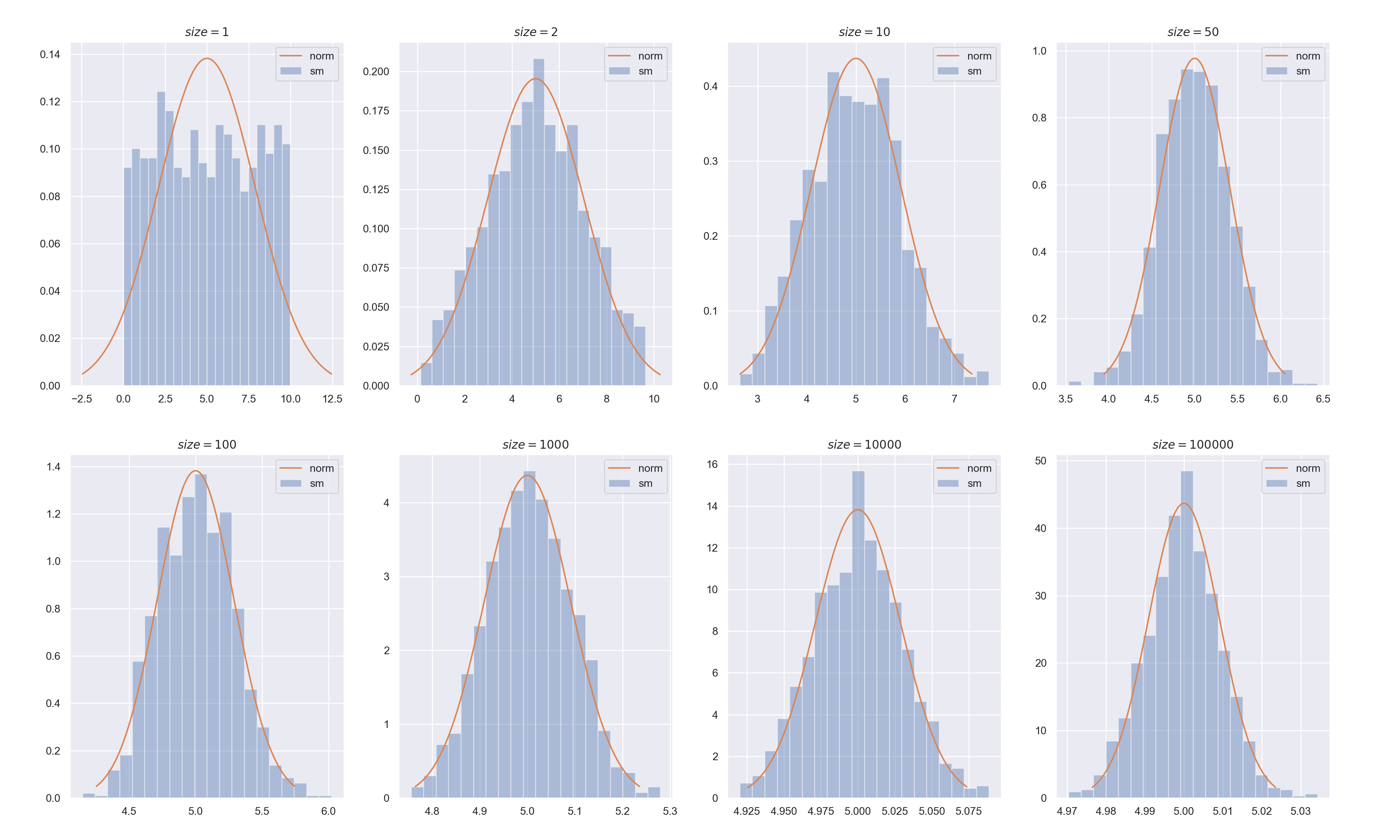
size が1のとき（左上）は，1つの標本しか取ってないので，中心極限定理で従うとされる正規分布（オレンジ色）とは大きく異なる分布（青色）になっています．
size が2あたりからオレンジ色の正規分布っぽい形に近づいてきます．
size を大きくすることで，標本平均が正規分布に従うことを確認できました．

二項分布

$X_1, \cdots, X_n$ が二項分布に従う場合を考えます．
具体的には $X_i \sim Bin(5,0.4)$ とします．

コードは一様分布の時とほぼ同じなので割愛します（scipy.stats.binom を使うように変えるだけです）．
結果は以下の画像です．

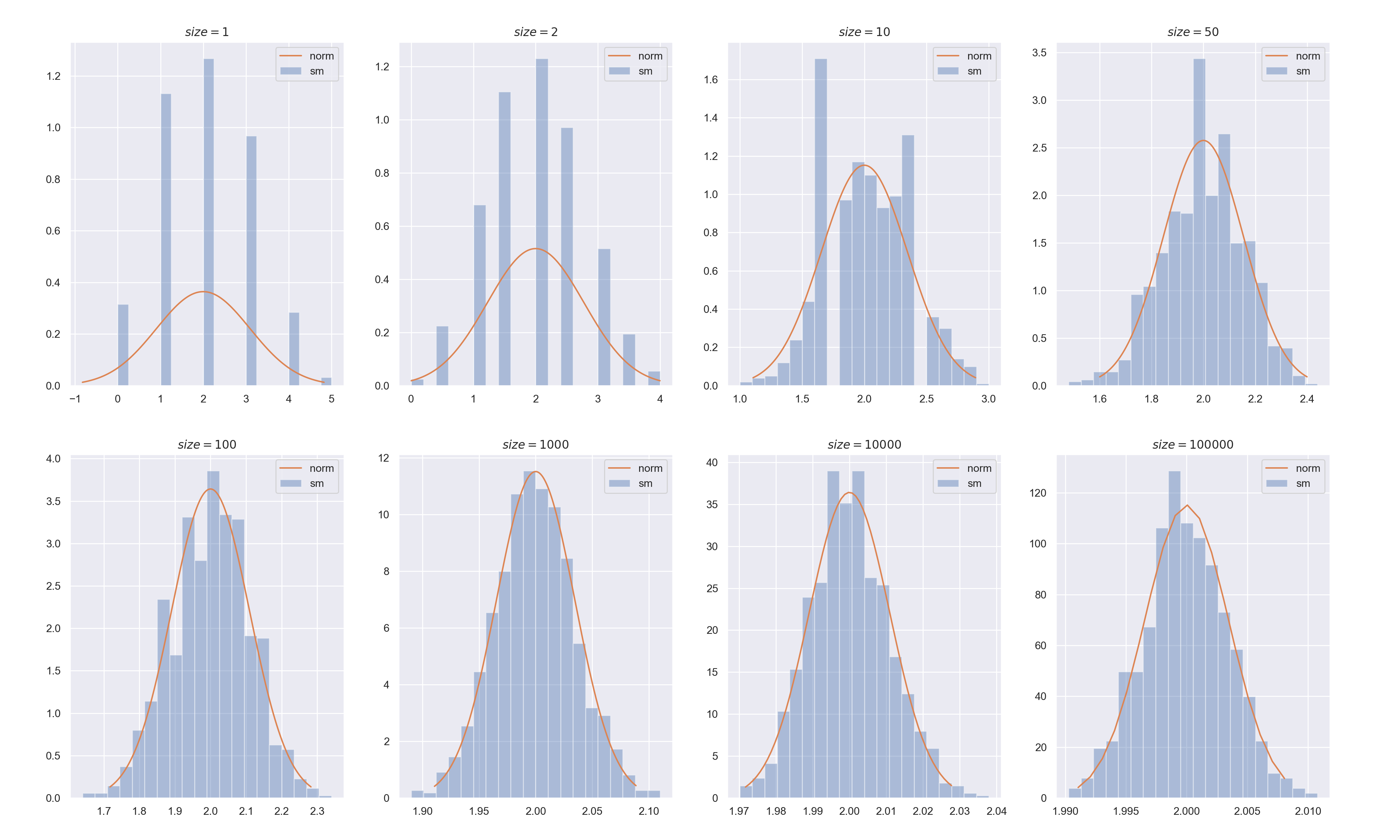
一様分布では size が2のときから標本平均のヒストグラムが正規分布っぽくなっていましたが，二項分布では size が50くらいから正規分布っぽくなっているように見えます．
size が1000以上のときはかなり標本平均が正規分布に近づいているのがわかります．

自作の確率分布

今度は一様分布や二項分布などのよく知られた分布ではなく，自作の簡単な確率分布を使って中心極限定理を確かめてみたいと思います．

設定
$X_i$ を $0,1,2,3$ という値を取る確率変数とします．
これらの値を取る確率がそれぞれ $0.1, 0.1, 0.3, 0.5$ であるとします（例えば $P(X_i=2)=0.3$）．
これは離散型の確率変数に対する確率分布になります．
この分布から取り出した標本平均の分布が，標本を大きくすることで正規分布に従うかを確かめます．

自作の分布からのサンプリング
サンプリングのために scipy.stats のモジュールが使えないので，numpy.random.choice を使います．
具体的には，np.random.choice(a=[0,1,2,3], size=100, p=[0.1, 0.1, 0.3, 0.5]) みたいにすれば，この確率分布から100個サンプリングできます．

コードはこのサンプリングの部分を変えるぐらいなので割愛します．
結果は以下の画像のようになりました．

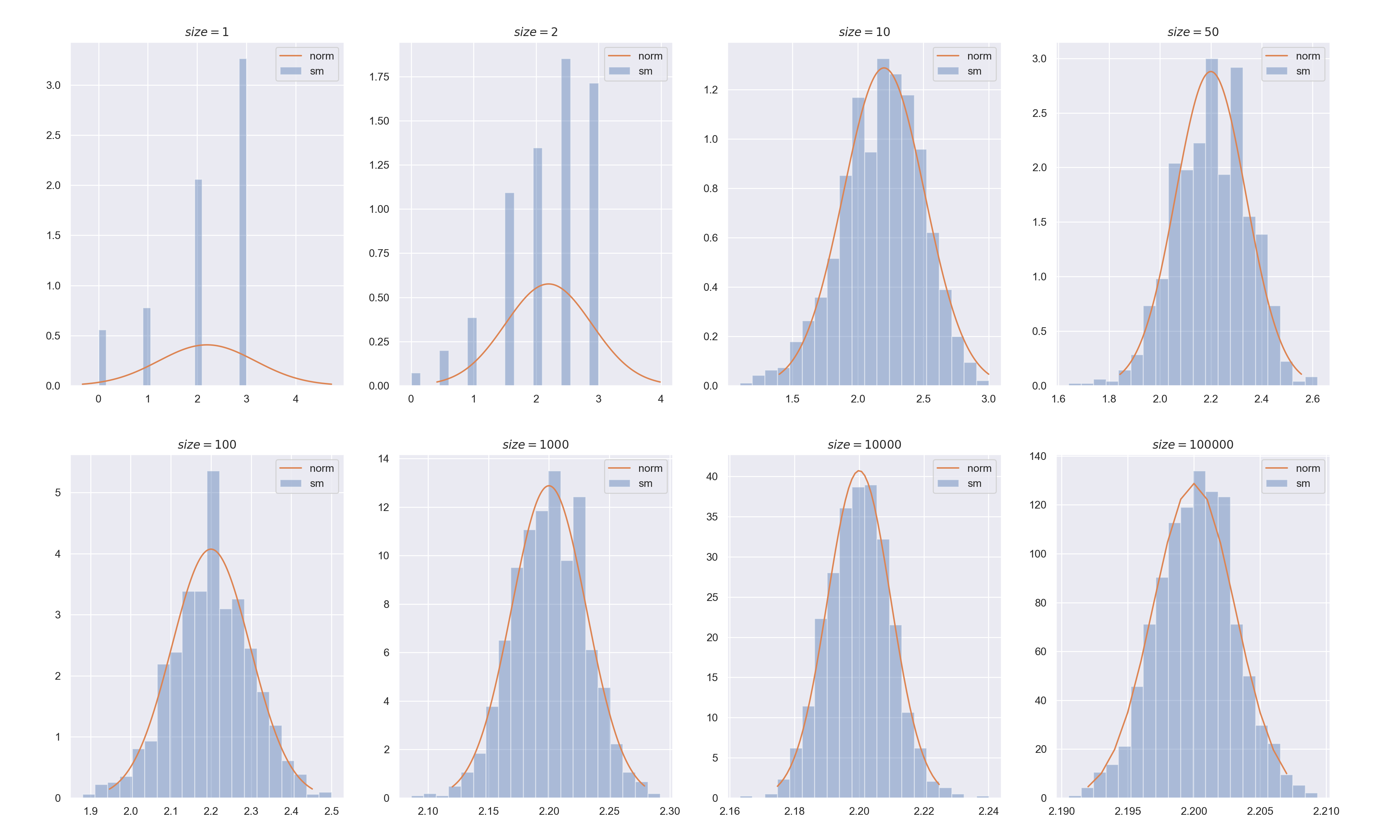
上で定めた確率変数は，3や2をの値を取る確率が比較的高い（それぞれ0.5, 0.3の確率）ので，size が1のときは横軸が3，次いで2が多くなっています．
size が10以上になったあたりから標本平均が正規分布に従っているように見えるので，この場合も中心極限定理を確認できました．

コーシー分布

最後にコーシー分布について確かめます．
コーシー分布に従う確率変数は期待値や分散が存在しません．
そのため，中心極限定理の前提である $E[X_i]=\mu, V[X_i]=\sigma^2$（有限の期待値，分散が存在すること）が成り立たないため，中心極限定理も成り立ちません．
これを実際に確かめてみます．

scipy.stats.cauchy の rvs という関数を使えばコーシー分布からのサンプリングができます．
コードはこれまで同様でサンプリングの部分が違うくらいなので割愛します．
結果は以下の画像の通りです．

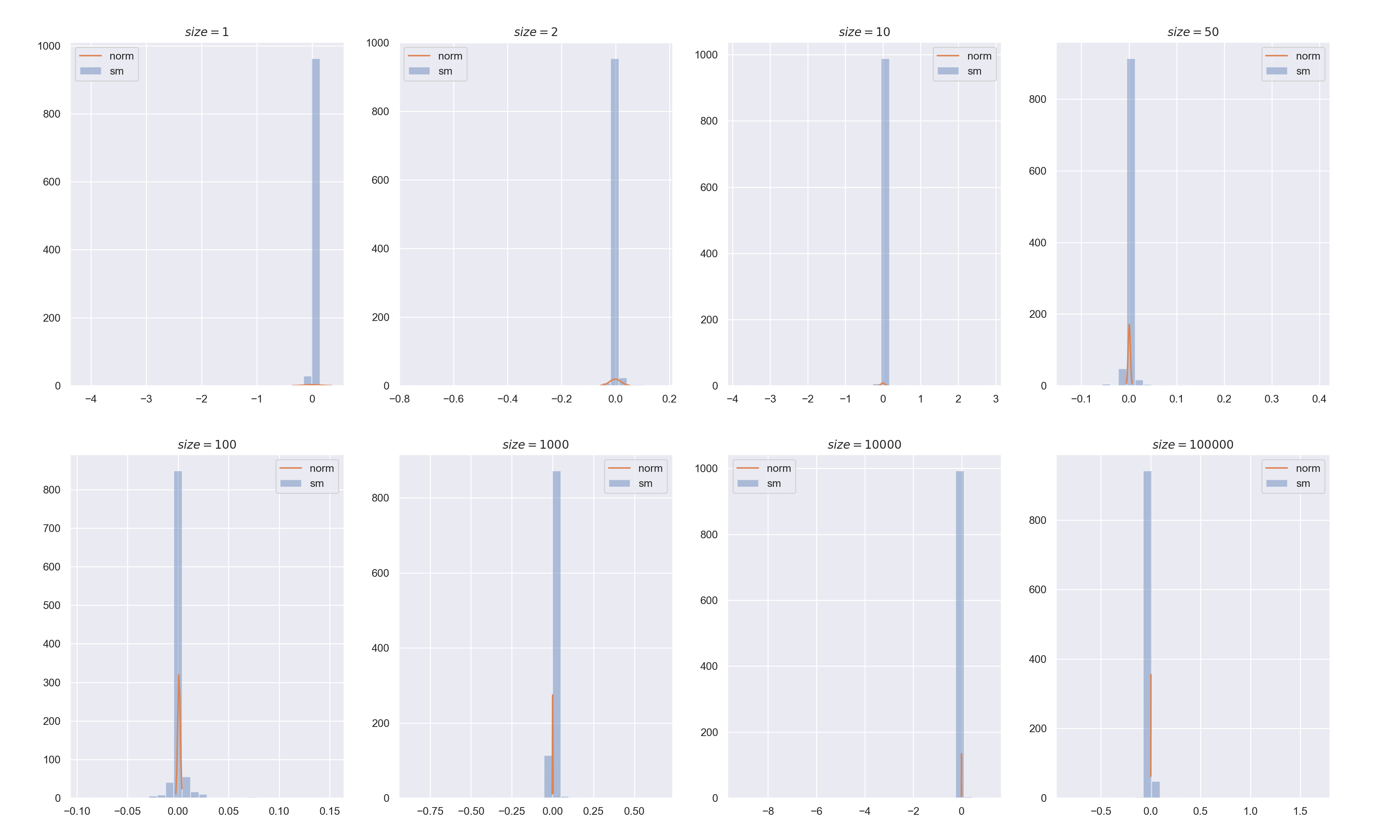
これまでの3つの分布とは大きく異なり，標本平均は正規分布に全く従っていないという結果になっています．
※ これまで正規分布（オレンジ色）のパラメータ $(\mu, \sigma^2/n)$ にはサンプリング元の分布の期待値，分散を使っていましたが，それらが存在しないため，標本平均，標本分散で代用してオレンジの線を描いています．

以上で中心極限定理が成り立つ3つの例と，成り立たない例まで確認できました．

中心極限定理を Python で確かめる（一様分布，二項分布，コーシー分布を使って）