Chainer Advent Calendarの11日目です。
コード進行認識とは
我々は音楽を作るとき、ピッチ(音高)が異なる音を重ねることでより豊かな響きを得ることができます。これをコード(Chord)と言います。時間が進むにつれてコードを変化(発展)させてゆくことで音楽の骨幹が出来上がっていきます。これがコード進行。
音楽を耳コピする際コード進行は最も重要な要素と言ってもいいでしょう。コード進行が分かればギターや鍵盤とかで伴奏をだいたい再現出来ちゃいます。
さて、要するに本文はコンピューターに自動耳コピさせようという話です。実際耳コピをするときなどは「この小節はAmが鳴っていて、次がCで…」というざっくりした感じで判断していきます。音符の羅列とかリズムとか細かいことは考えないですね。コードは構成音で明確に定義できるのですが、実際の音楽信号は周波数域に分解してみるとピッチが不明瞭だったり倍音が入り乱れたり非構成音も普通に混ざるので判別は容易ではありません。ゆえにデータ駆動な方法に頼りがちなのが現状です。
音楽情報処理(MIR)界隈では基本的なタスクの一つで、ジャンル判別、感情分析やカバーソング認識などに役立ちます。毎年行われる音楽情報処理競技MIREXのタスクの一つでもあります。
MIREX 2016:Audio Chord Estimation
参戦したアルゴリズムまとめ
まあ、形式的には何の変哲もない普通の系列ラベリング問題ですので、コード進行認識に限らず、色んな類似したタスクの実装の参考になればと思います。
NNの実装はChainer、そして前処理にlibrosa、正答率の計算にmir_evalというライブラリを使います。
入力の前処理
NNの入力は、音楽信号のスペクトラム系列(あるいはスペクトログラム)です。手順は前処理も含めると、
- 音楽信号の打楽器成分を分離する。ジャマな打楽器音は消しましょう。librosaで一発です。
- Constant-Q Transformする。スペクトラム変換と言えばフーリエ変換(STFT)ですが、フーリエ変換は「周波数域が線形」と「(窓が固定長ゆえに)周波数ごとに分解能が違う」という問題を抱えています。音楽信号はピッチ情報が肝心なので対数周波数域で表示するのが望ましいです。FFTスペクトラムを圧縮して対数周波数域に変換することもできますが、ここでは分解能が変わらないように周波数ごとに窓の長さが変化するCQTを使います。~~どうせlibrosaなら一発。~~1オクターブごとに24次元(つまり1次元ごとに1/2半音)、C0のピッチから6オクターブ分のスペクトラムを計算してもらったので144次元のベクトルになります。数字の選択はわりと適当です。
- logarithmic compressionする。f(X)=log(1+X)という風に変換します。ベクトル値を対数域に変換してノイズを抑える前処理です。ちょっとロバストになるそうです。
- 隣り合わせのベクトルを連結して大きなベクトルにします。例えば時間tのベクトルがあるとすると、t-3からt+3まで(足りない場合はパディング)の、計7つのベクトルを連結して1008(=144x7)次元の入力ベクトルに変換します。入力サイズも7倍に膨れ上がりますが認識がさらに安定するようです。
(*文末の補足も参照!)
さて、この一次元ベクトルの系列(DNNにとっては系列というより集合)をDNNに放り込んてやりましょう。
DNN-CRFモデル
スペクトラム系列のラベリングを学習するNNを作ります。DNNでフレームごとの分類をして、それをCRFに送ってラベル系列のコンテキストも加味して系列の尤もらしさを求めて最終的なラベル系列を出力するという寸法です。
ではNNを書きます。Chainerのバージョンは、CRFを使ってるので1.13以上であれば問題ないでしょう。Pythonは2.7系です。
隠れ層数やユニット数を手軽に制御できるようにしたいのでDNNの定義はChainListを使います。
まあ、普通に全結合層を重ねるだけのやつですね。学習方法はMNISTの例と同じなので特に説明は不要でしょう。
class DNN(ChainList):
def __init__(self,links):
super(DNN,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
h = x
for i in xrange(self.__len__()-1):
li = links.next()
h = F.dropout((F.relu(li(h))),train=self.train)
y = links.next()(h)#最終段は線形変換
return y
そしてCRFの定義。Chainerに実装されているのは自然言語処理で人気らしいlinear-chain CRFという、ひとつ前のラベルのみを素性としたモデルです。DNNの出力を入力とします。
class CRF(Chain):
def __init__(self):
super(CRF,self).__init__(crf=L.CRF1d(N_CLASSES))
def __call__(self,list_x,list_t):
self.loss = self.crf(list_x,list_t)
return self.loss
def argmax(self,list_x):
~,path = self.crf.argmax(list_x)
return np.array(path,dtype="int32").flatten() #pathはバッチの配列になってるので変形
改めて見ると新クラスを作る意味がほぼ無いですね・・・まあいいか。
CRFに入力を送る時は、Variableを配列にまとめる必要があります(ドキュメント曰くlist of Variable)。学習時はさらにバッチにまとめると高速化できます。
自分の場合下のように書きました。Yはあらかじめ計算したDNNの出力で、全部1バッチに収めているのでshape=(seqsize,25)の配列です。Tは正解ラベル系列。
# 学習ループの一部です
startidx = np.random.randint(0,seqsize-256-1,size=16*100)#系列の起点をランダムに決める
for i in range(0,32*100,32):
x_batch_list = [Variable(cp.asarray(Y[startidx[i:i+32]+j,:])) for j in range(256)]
t_batch_list = [Variable(cp.asarray(T[startidx[i:i+32]+j])) for j in range(256)]
opt.update(crfmodel,x_batch_list,t_batch_list) #cpはcupyです
要するに、毎回ランダムに長さ256の系列を32個取って一つのバッチにまとめて、CRFに与えるという流れです。
最新バージョンでCRF1dは長さが異なる系列もバッチで扱えるようになったようですが、ここでは長さ256で固定しています。書きやすいし。
DNNとCRFをひとつのChainに入れて一緒に学習させることもできますが、ここでは二歩に分けてます。まず訓練データを使ってDNNのみを訓練します。損失関数はsoftmax_cross_entropy。
それが終わったらDNNのパラメーターを固定してCRFを学習させます。
ラベル推定の時は、DNNの出力の系列を与えればCRF1d.argmax()がViterbi探索で最尤ルートを返してくれます。べんりー。
ラベルの種類
最も簡単なMajMinルールでいきます。セブンスなどは無視して、メジャートライアド、マイナートライアド各12個に加えて、No Chord(無音や単音、パーカスのみの区間など)という特殊なラベルを入れて、計25種類です。
ハイパーパラメータ
DNNのパラメタは論文などを参考にして適当に選んでます。
- 最適化アルゴリズム:AdaDelta
- 入力次元数:1008(=144x7)
- 隠れ層数:4
- 隠れ層ユニット数:512
- Dropout率:0.5
CRFの最適化もAdaDeltaです。
データセット
データセットに使うのはisophonics.netが公開しているコード進行のアノテーションです。Beatles全アルバム、Queenのベスト盤とKalore Kingアルバムの一部で、約200曲の量です。
アノテーションの表記はこんな感じ。
0.000000 0.175157 N
0.175157 1.852358 C
1.852358 3.454535 G
3.434535 4.720022 A:min
...
...
DNNによる認識結果もこの表記で出力すれば、mir_evalによる正解率計算および認識結果の可視化ができます。
データセットはランダムに5:1くらいに分割してtrain setとtest setにします。Cross validationとかはめんどいのでやりません。validate setとかも無し。
分類問題なので、評価基準は正答率=(推定ラベルが正解した時間の総和)/(音楽の長さの総和)です。推定結果をisophonicsのデータセットと同じテキスト形式で出力してから、mir_evalライブラリで正答率を計算してもらいました。
性能評価
学習済みのDNNのtest setとtrain setの分類精度、そして学習済みのCRFと組み合わせた最終的な認識精度を測りました。
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 77.0% | 68.4% | 84.7% | 76.6% |
CRFが系列ラベリングの精度に大きく寄与してるのがわかります。
認識結果をAudacityに可視化してもらうとこんな感じ。ビートルズのHere Comes The Sunのコード進行(一部)です。下が認識結果で、上が人手による正解。細かいコードの変化は捉え切れてないものの、だいたい上手くいってるのがわかります。
Residualにしてみる
折角なのでDNNをResNet風に改造してみましょう。
ChainerによるResNet風改造は超簡単。ゆえにChainerは最強。
class DNNRes(ChainList):
def __init__(self,links):
super(DNNRes,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
li = links.next()
h = F.relu(li(x)) #入力層からの変換はResにしない
for i in xrange(self.__len__()-2):
li = links.next()
h = F.dropout(F.relu(li(h)),train=self.train)+h #ここに+hを加えるだけ
y = links.next()(h)
return y
本家ResNetは二つの隠れ層で一つのResidual Blockにしてるみたいですがめんどくさい分かりやすさ優先して一層ごとにResidualにしちゃいます。複数層の場合はResidual Blockを別途クラス(Chain)で作った方がいいでしょう。
隠れ層数もどかんと20層に。過適合がひどかったのでDropoutの他に少し強めのWeight Decayを加えました。係数0.001。
結果!
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 78.8% | 74.0% | 85.5% | 80.5% |
| かなりtest setの精度が良くなりましたね。80%の大台いきました。 |
今年のMIREXの結果は最高86%くらいまであるのでまだまだですが、他と比べてもなかなか健闘できてます(Cross validationじゃないので厳密には比較できないのですが)。
CRFの実装について
(linear-chain)CRFについてはこの記事やこの記事(英文)の紹介がオススメ。
CRFは、
P(Y|X)=\frac{\exp{E(X,Y)}}{\sum_{Y'}{\exp{E(X,Y)}}}
という風にラベル系列Yの条件付確率を求めるわけですが(-logをかけると損失関数になる)、素性関数E(X,Y)の定義は色々あります。
Chainerの場合は(ドキュメントから推測)、
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i})}
と、単純にフレームのクラス損失x(DNNなどで計算してもらう)とラベル遷移コストcを足し合わせるだけです。この場合学習するパラメータはラベル遷移コストの行列cのみ。
これに上段のDNNを組み込んで(Xはスペクトル系列とみなすと)、
E(X,Y)=\sum_i{(f_{dnn}(x_{iy_i})+c_{y_{i-1}y_i})}
って書くとそもそも全体で一つのでっかいCRFだったとも言えるかも?
というかもういっそラベル遷移コストも非線形化して、
E(X,Y)=\sum_i{(f_{dnn_1}(x_{iy_i})+f_{dnn_2}(c_{y_{i-1}y_i}))}
ってしちゃうのもアリかもしれない。だんだんRNNに寄ってる気がするけど。
ほかの論文を見ると、
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i}+b_{y_i})}+\pi_{y_0}+\gamma_{y_N}
という風に、バイアスbがついてたり、ラベル系列の先頭、末尾のポテンシャル(グローバルな特徴)を組み込んだりするのを見かけます。これはChainer実装をちょっといじれば実現できそう?
品詞タグ付けのタスクになると、接尾辞(-lyなど)に関する場合分け関数にしたりもするようです。
このように、識別モデルであること(条件付確率を直接求める)、素性関数が柔軟(グローバル特徴やヒューリスティックなルールも組み込める)、パラメータ値の制約がない、という所が、同じタスクでよく使われてたHMMとの違い。
何よりパラメタが微分可能であれば勾配降下で学習できるのでNNと相性がいい!最強!ゆえに系列ラベリングのタスクで応用が広がってるようです。Chainerも今後バリエーションが増えることに期待。
*補足:今回の例での行列cをプロットしてみました。
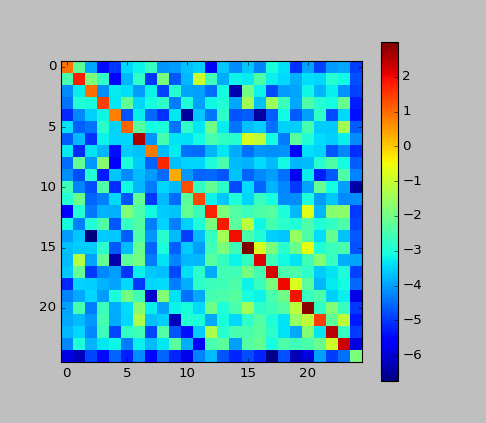
主対角線の値が高いことから、CRFは「ラベルの変化を抑える方向に働いている」という事がわかります。HMMでも大体そんな感じでしたね。
まとめ
完全なソースコードはちょっと人に見せられる出来ではないのでご容赦ください。
自動耳コピという課題で研究生をやっているので、(MIR分野の布教も兼ねて)ある程度分かったことを今回紹介してみました。形式的には本当に単純な系列ラベリング用のモデルですが、それでもコード進行認識というタスクではなかなか良い性能が出せるようです。
その気になればDNNをもっと深くしたりCNNにしたり、何ならRNNにしてみたりもできます。
自分は現在もうちょっと複雑なモデルも作ってるんですが論文書いてる最中なのでまた今度紹介できたらと。
Chainerずっと使ってますがほんとに良いです。思い描いた形通りに組み立てていける感が超気持ちいいし助かる。ゆえに最強(二回目)。
補足:正規化忘れてた
前処理で入力の正規化をすっかり忘れてました。なんてこった。やりなおし。
前処理のstep3(対数変換)と4の間に正規化を挟みます。やり方は色々あると思いますがここではglobal mean variance normalizationでやります(一曲分のスペクトログラム全体のmeanとvarを求める)。
norm(X)=\frac{X-mean(X)}{var(X)}
平均値0、分散1というNNが喜ぶ形に変換。
あと、step3のいわゆるlogarithmic compressionも見直しました。この処理は元々、同じタスクでよく使われるChromagramという特徴量のノイズを圧縮するための前処理なんですが、Chromagramは非負なので、対数変換する際+1して性質を保つ必要がありました。
別のディープラーニングな論文でスペクトログラムの前処理にも使ってたんで真似したのですが、考えてみたら入力の値域を非負に限定する必要は無いわけで、ならば+1して値域を圧縮してしまうのは勿体ない。
なので+1は要らない。
f(X)=log(0.01+X)
普通にlogをかければOK。0.01はゼロ値回避用。
これをResidual DNN-CRFの設定でやり直してみました。
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 84.8% | 77.4% | 88.6% | 82.0% |
| だいぶ伸びましたね。 | |||
| やっぱり前処理は大事。正規化は大事。みんなも気を付けよう! |
