はじめに
現在のコロナ禍において,多くの人がワクチンを接種することは,感染症の拡大を防ぐために有効であることが示されてきました.しかし,ワクチンが限られた数しか提供できない場合,どの順番で打つと効果的なのかという問題が出てきます.そのような話はtargeted vaccination(対象を絞ったワクチン接種)の問題として研究されたりしています.
この記事の著者の@igenkiと@wsotatataは,この話をシミュレーションで検証されている文献[1]の記事に感銘を受け,自分たちでシミュレーションのプログラムをPythonで作ってみることにしました.本記事では,そのプログラムの作成と文献[1]のシミュレーションの再現結果について書いていきます1.
感染症が拡がるネットワーク
まずは人と人の間で感染症が拡がる状況を想定します.人と人の間のつながり(家族,友人,同僚など)が濃いほど,感染症はその人達の間で拡がる可能性が高いでしょう.このつながっている人たちの関係性は,以下の図のように,人をノード(頂点),人と人の間のつながりをエッジ(辺)でつないだネットワークで考えることができます.
図1.人々のつながり(=ネットワーク)
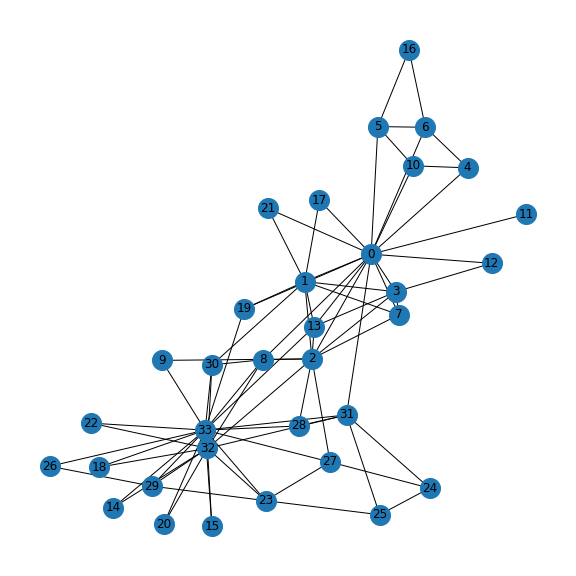
では,このようなネットワークの中で感染症が拡がることを考えましょう.具体的なネットワークとしては文献[1]で例として使用されている空手クラブのネットワークを使います.このネットワークはZachary's Karate Club graphと呼ばれているアメリカのある大学の空手クラブ間の交友関係を示したものです2.
Pythonベースのネットワークの分析のツールであるNetworkXには,この空手クラブのデータがデータセットとして含まれています.早速このネットワークをNetworkXで可視化してみましょう3.最初に,このシミュレーションで必要となるモジュールを一気にインポートしておきます.
必要モジュールのインポート
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import random
import pandas as pd
import time
空手クラブのネットワークの可視化は以下のコードでできます.
空手クラブネットワークの可視化
np.random.seed(20) # シード値を20に固定すると下の図になります
G = nx.karate_club_graph()
plt.figure(figsize=(8,8))
nx.draw_spring(G, node_size=400,with_labels=True)
plt.show()
図2.Zachary's Karate Club graph
図2のようにノード(人)の数が34で,エッジ(交友関係)の数が78のネットワークが作成できました.
感染症のシミュレーション
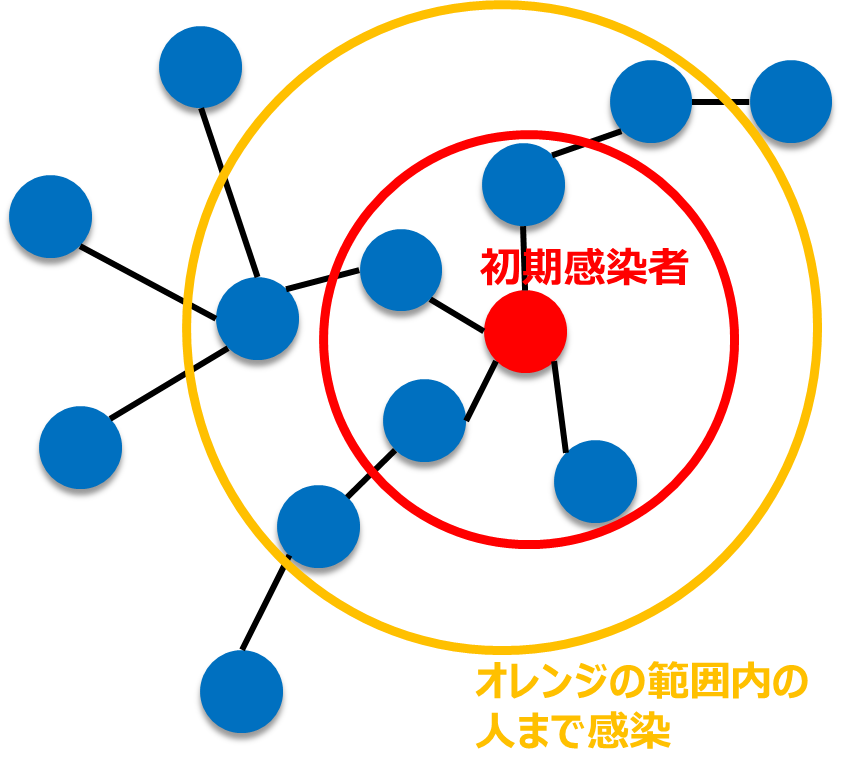
では,この空手クラブネットワーク上で感染症が拡がる状況をシミュレーションします.感染症は以下の簡単なプロセスで拡がることを仮定します.文献[1]と同様の設定です.
ランダムに選んだ1人を初期感染者とし,初期感染者から2ステップ先までつながっている人を感染させる.感染はそれ以上は拡がらない.
つまり,感染症は初期感染者からつながっている人達にさらにつながっている人達まで拡がるという仮定です.図にすると以下のようになります.
図3.簡単な感染症のモデル
モデルの説明をしたところで,実際にシミュレーションして,感染者数平均を算出します.上記のように,初期感染者は全てのノードからランダムに選択し,その感染者ノードから2つ先の隣接ノードまでのノード数を数え,感染者数を求めます.初期感染者はランダムに選ばれますので,毎回結果が異なります.したがって,反復回数を100回としてその感染者数の平均値を最終的に算出します.まずは,誰もワクチンを接種していないモデルで実験してみましょう.
ワクチンなしの感染症シミュレーション
T = 100 # 反復回数
I_num_list = [] # 感染者数のリスト
for _ in range(T):
node = random.randint(0,nx.number_of_nodes(G)-1) # 最初の感染者をランダムに選択
I_list = [node] # 感染者リストの生成
I_list.extend(list(G.adj[node])) # 最初の感染者の隣接ノード(1次感染者)を感染者リストに格納
I_list = list(set(I_list)) # 重複している感染者ノードを1つにまとめる
search_list = I_list[:] # 2次感染者を探すためのリストを現在の感染者リストからコピー
search_list.remove(node) # 2次感染者を調べるノードから最初の感染者を除く
for v in search_list: # 2次感染者を調べていく
I_list.extend(list(G.adj[v])) # 2次感染者を感染者リストに格納
I_list = list(set(I_list)) # 重複している感染者ノードを1つにまとめる
I_num_list.append(len(I_list)) # あとで感染者数平均を求めるために感染者数をリストに追加する
I_ave = np.average(I_num_list) # 感染者数平均を求める
print("感染者数平均:" + str(I_ave))
>>>
感染者数平均:21.22690763052209
まず,コードの説明からします.最初の感染者となるノードの番号を乱数で選び,変数nodeに格納します.変数I_listには感染者となったノードの番号をリストにして保存していきます.例えば,0番のノードと4番のノードが感染者の場合,I_list=[0,4]になります.次に,1次感染者を感染者リストI_listに格納していきます.1次感染者は,最初の感染者の隣接ノードG.adj[node]で見つけることができるので,I_list.extend(list(G.adj[node]))とすることで1次感染者を感染者リストに格納します.次に,2次感染者を見つけます.そのためには,1次感染者の隣接ノードを調べたいので,1次感染者のリストsearch_listを作ります.このsearch_listの隣接ノードを感染者とし,重複しているノードを一つにまとめ,そのリストの長さから総感染者数を求め,総感染者数のリストであるI_num_listに追加します.これを100回繰り返して,最後にI_num_listの平均をとり,感染者数平均I_aveを求めます.
ワクチンなしで実験した結果,感染者数平均は約21.23人となり,文献[1]に載っていた結果とも一致しました.この数字が,人々がワクチンを打つことでどれだけ減少するのかを見ていきます.
ワクチンを1人だけ打つシミュレーション
最初に,ワクチンが1本だけあり,1人だけそのワクチンを打てる場合からシミュレーションしてみます.ワクチンを打った人は100%感染しないと仮定します.どの人にワクチンを打つのが最適(感染者数を最も減らすことができる)なのか,すべてのノードを1つずつ試してみましょう.
T = 100
I_min = 100000 # 感染者数平均の最小値を格納するため,初期値は無限大にしておく
I_ave_list = []
for i in range(nx.number_of_nodes(G)): # ワクチン接種者を全ノードで試す
vaccinated = i
I_num_list = []
for _ in range(T):
node = random.randint(0,nx.number_of_nodes(G)-1)
if node == vaccinated: # 最初の感染者がワクチン接種者の場合
I_num_list.append(0) # この場合の感染者数は0
else:
I_list = [node]
I_list.extend(list(G.adj[node]))
I_list = list(set(I_list))
if vaccinated in list(G.adj[node]): # 最初の感染者の隣接ノードにワクチン接種者がいる場合
I_list.remove(vaccinated) # ワクチン接種者を感染者リストから除く
search_list = I_list[:]
search_list.remove(node)
for v in search_list:
I_list.extend(list(G.adj[v]))
I_list = list(set(I_list))
if vaccinated in I_list: # 2次感染者にワクチン接種者がいる場合
I_list.remove(vaccinated) # ワクチン接種者を感染者リストから除く
I_num_list.append(len(I_list))
I_ave = np.average(I_num_list)
I_ave_list.append(I_ave)
if I_min > I_ave:
I_min = I_ave
vac_min = vaccinated
print(f"最小値のノード:{vac_min} 感染者数平均の最小値:{I_min}")
>>>
最小値のノード:0 感染者数平均の最小値:14.84
大部分は「ワクチンなし」のコードと同じなので,書き加えた部分にコメントを加えました.ワクチン接種者を区別するため,新しい変数vaccinatedを追加しました.感染者リストにワクチン接種者が格納された場合に,ワクチン接種者をリストから外すという処理を加えています.もし,最初の感染者にワクチン接種者が選ばれてしまった場合には,感染者数は0になります.
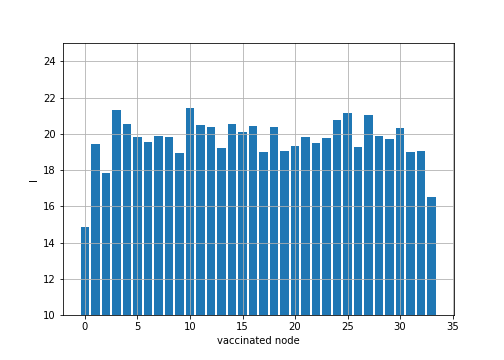
この結果から,ワクチンが1本の場合では,0番のノードにワクチンを与えると,感染者数平均を最小にできることがわかりました.ワクチンなしの感染者数21.23人の場合と比べると,0番のノードにワクチンを与えることで感染者数を平均で14.84人に抑えることができています.図2を見ると0番のノードは多くの人とつながっているので,このノードがワクチンを打つと感染症が拡がらないということは妥当な結果です.また,各ノードごとの感染者数平均をグラフにしたものを以下にまとめておきます.
図4.ワクチンを打つノードと感染者数平均Iの値の関係
ワクチンを2人だけ打つシミュレーション
次に,ワクチンは2本存在し,2人の人がそのワクチンを打てる状況で,シミュレーションしてみます.コードと結果は以下のとおりです.
N = 2 # ワクチンの本数
T = 100
I_min = 100000
t1 = time.time() # タイマー開始
for j in range(nx.number_of_nodes(G)):
for i in range(nx.number_of_nodes(G)):
if i == j or i > j: # 同じ組み合わせを省略
continue
else:
vaccine_list = [i,j] # i番のノードとj番のノードがワクチン接種者
I_num_list = []
for _ in range(T):
node = random.randint(0,nx.number_of_nodes(G)-1)
if node in vaccine_list:
I_num_list.append(0)
else:
I_list = [node]
I_list.extend(list(G.adj[node]))
I_list = list(set(I_list))
for v in range(len(vaccine_list)): # ここをvaccine_listに変更,リスト内の要素すべてを調べる
if vaccine_list[v] in list(G.adj[node]): # ワクチン接種者が初期感染者の隣接ノードである場合
I_list.remove(vaccine_list[v])
search_list = I_list[:]
search_list.remove(node)
for v in search_list:
I_list.extend(list(G.adj[v]))
I_list = list(set(I_list))
for v in range(len(vaccine_list)): # ここもvaccine_list
if vaccine_list[v] in I_list: # 感染者リストにワクチン接種者がいる場合
I_list.remove(vaccine_list[v]) # ワクチン接種者を感染者リストから除く
I_num_list.append(len(I_list))
I_ave = np.average(I_num_list)
if I_min > I_ave:
I_min = I_ave
vac_min = vaccine_list
t2 = time.time() # タイマー終了
print(f"計算時間:{t2-t1}")
print("最小値の組:" + str(vac_min) + " 感染者数平均の最小値I:" + str(I_min))
>>>
計算時間:1.01730632781982422
最小値の組:[0,33] 感染者数平均の最小値:11.06
「ワクチン1本」のコードとの差分は変数vaccinatedがリストvaccine_listになった点です.同様に,変更点にはコメントを加えています.変数$i, j$をワクチン接種者の組と捉え,すべての組み合わせで計算していきます.今回は計算時間も計測します.ワクチンが2本の場合,ノード番号0と33にワクチンを与えると,感染者数平均を最小にできることがわかりました.図4の棒グラフからも,0と33にワクチンを与えるのが良さそうだと推測できそうです.3本,4本の場合も同様に実装し,どの組み合わせが良いのかを見ていきます.
結果1.ワクチン1~4本
ワクチンの本数を4本まで変えて,シミュレーションした結果が下の表になります.
| 本数 | 頂点の組 | 感染者数平均 | 計算時間 |
|---|---|---|---|
| 1 | [0] | 14.84 | 0.060836 |
| 2 | [0,33] | 11.06 | 1.017306 |
| 3 | [0,32,33] | 7.10 | 11.215391 |
| 4 | [0,2,32,33] | 4.27 | 92.371320 |
本数が4本で,どの人にワクチンを打つのが良いかが分かると,感染者数平均を4.27人に留めることができました(全ノード数は34).しかし,最適なワクチン配置を見つけるために,ワクチンを与えるノードのすべての組み合わせを計算(全列挙)していると,ワクチンの本数が10本,20本と増えてきた場合には現実的な時間で計算を終えることができません.そこで,文献[1]で行われたように,**中心性(centrality)**というネットワークにおける各ノードの重要性を測る指標を用いて,どの人にワクチンを打つのが良いかを同様に考えてみましょう.
中心性
中心性は,ネットワークの中で中心的なノードを見つける時に役に立つ指標です.今は感染症の話をしているので,中心的な人とは感染症を拡げてしまう人と解釈します.したがって,この感染症拡大の中心となっている人にワクチンを打つことができれば(打ってもらえれば),感染症の拡大を抑制することができるでしょう.中心性と呼ばれる指標は複数あります.ここでは,次数中心性,媒介中心性,近接中心性,固有ベクトル中心性の4つを取り上げます.それぞれの中心性の指標の定義と具体的な計算方法が知りたい方は,@igenkiが以前に書いた以下の記事をご参照ください.
次数中心性
各ノードが持つエッジの数(=次数)が次数中心性です.まずは,次数中心性が高いノードを上位5つ取り出してみます.NetworkXにおける次数中心性の計算は nx.degree_centrality(G) で求めることができます.
print(sorted(nx.degree_centrality(G).items(),key=lambda x: x[1],reverse=True)[:5])
>>>
[(33, 0.5151515151515151), (0, 0.48484848484848486), (32, 0.36363636363636365), (2, 0.30303030303030304), (1, 0.2727272727272727)]
33番のノードが0.51515...,0番のノードが0.48484...,といったように次数中心性が高い順に5つ取り出せました.数字は$N-1$で割って規格化されています.ここで得られた5つのノードの組 [0,1,2,32,33] をワクチン接種者として,同様に実験してみましょう.コードは以下のとおりです.
N = 5
T = 100
t1 = time.time()
vaccine_list = []
v_tuple = list(sorted(nx.degree_centrality(G).items(),key=lambda x: x[1],reverse=True)[:N]) # ここで中心性の上位5つを求める
for v in list(v_tuple):
vaccine_list.append(v[0]) # 5つのノードのワクチン接種者リスト
print(f"ノードの組 {vaccine_list}")
I_num_list = []
for _ in range(T):
node = random.randint(0,nx.number_of_nodes(G)-1)
if node in vaccine_list:
I_list = []
I_num_list.append(len(I_list))
else:
I_list = [node]
I_list.extend(list(G.adj[node]))
I_list = list(set(I_list))
for v in range(len(vaccine_list)):
if vaccine_list[v] in list(G.adj[node]):
I_list.remove(vaccine_list[v])
search_list = I_list[:]
search_list.remove(node)
for s in search_list:
I_list.extend(list(G.adj[s]))
I_list = list(set(I_list))
for v in range(len(vaccine_list)):
if vaccine_list[v] in I_list:
I_list.remove(vaccine_list[v])
I_num_list.append(len(I_list))
I_ave = np.average(I_num_list)
t2 = time.time()
print(f"感染者数平均:{I_ave}")
print(f"計算時間:{t2-t1}")
>>>
ノードの組 [33, 0, 32, 2, 1]
感染者数平均:2.61
計算時間:0.0019941329956054688
次数中心性が高い上位5つのノードで実験した結果,感染者数平均は2.61,計算時間は約0.00199秒と求まりました.
媒介中心性,近接中心性,固有ベクトル中心性
次数中心性を求める部分 nx.degree_centrality(G) をそれぞれの中心性に書き換え,媒介中心性,近接中心性,固有ベクトル中心性も同様にシミュレーションしていきます.簡単にそれぞれの中心性が何を表すかを説明しておきます.媒介中心性は,注目しているノードがそれ以外の2つのノード間の最短経路にどのくらいの割合で入っているかを数値にしたものです.近接中心性は,あるノードから他の全てのノードへの距離(最短経路長)の平均値の逆数をとったものです.固有ベクトル中心性は,中心的なノードとつながっているノードを中心的であるとみなす指標です.それぞれの中心性は,NetworkXで次の表の書き方で計算できます.
| NetworkX | |
|---|---|
| 次数中心性 | nx.degree_centrality(G) |
| 媒介中心性 | nx.betweenness_centrality(G) |
| 近接中心性 | nx.closeness_centrality(G) |
| 固有ベクトル中心性 | nx.eigenvector_centrality(G) |
結果2.中心性と全列挙との比較
ワクチン5本をそれぞれの中心性が高い上位5つのノードに与えて実験した結果をまとめた表が以下になります.全列挙は,これまでと同様に,すべてのノードの組み合わせを計算し,最も感染者数平均が少なかったノードの組で実験を行ったときの結果を表しています.結果の表から以下のことがわかりました.
- 中心性が高い頂点の組は,全列挙の頂点の組に近い組を取っている.特に,次数中心性と固有ベクトル中心性の組は全列挙と全く同じ組み合わせとなった.
- 計算時間を見ると,全列挙は約10分かけて最適な組み合わせを見つけているが,中心性を用いることで圧倒的に短い時間で,かつ効果的な感染者数平均の値を求めることができる.
- 感染症の制御には次数中心性と固有ベクトル中心性が効果的である可能性がある.
| 頂点の組 | 感染者数平均 | 計算時間 | |
|---|---|---|---|
| 次数中心性 | [0,1,2,32,33] | 2.61 | 0.00199 |
| 媒介中心性 | [0,2,31,32,33] | 3.51 | 0.00696 |
| 近接中心性 | [0,2,8,31,33] | 6.12 | 0.00798 |
| 固有ベクトル中心性 | [0,1,2,32,33] | 2.71 | 0.00499 |
| 全列挙 | [0,1,2,32,33] | 2.66 | 607.04313 |
まとめ
本記事では文献[1]で紹介された中心性を使った感染症の制御のシミュレーションの内容を自分たちで再現するためにPythonのプログラムを作成しました.プログラム全体はGitHub においてあります.実際にシミュレーションしてみた結果,文献[1]で紹介されたのと同様の結果を得ることができました.全探索をしなくても,中心性を使うことで,全探索に劣らない効果的なワクチン配置(どの人を優先してワクチンを打つべきか)を見つけることができることが分かりました.文献[1]があって,私達はこの記事を書こうと思いました.この記事を私達が書く動機となった文献[1]にあらためて感謝いたします.
参考文献
[1] 小蔵正輝, 中心性を使った感染症の制御, 経済セミナー, no. 717, pp. 42-46, 2020. [html]
-
文献[1]の著者の方から,この記事の公開について許可をいただきました.深く感謝いたします. ↩
-
特にこの空手クラブで感染症が過去に流行ったというわけではなく,仮にこのネットワークで感染症が拡がる状況を想定するというだけです. ↩
-
NetworkXでは,実際のデータからネットワークを作ったり,自分で一からネットワークを作ったりもできます.自分で一から作る方法は@igenkiが以前に書いたNetworkXによるネットワークの作成と可視化で紹介しています. ↩