ネットワークの中心性（媒介中心性と固有ベクトル中心性）

前回の記事（次数中心性と近接中心性）に引き続きネットワークの中心性について説明していきます．今回は，媒介中心性と固有ベクトル中心性の2つです．これまでに書いたネットワークの記事

• NetworkXによるネットワークの作成と可視化
• NetworkXによるモデルからのネットワーク生成

も併せてご覧ください．

媒介中心性

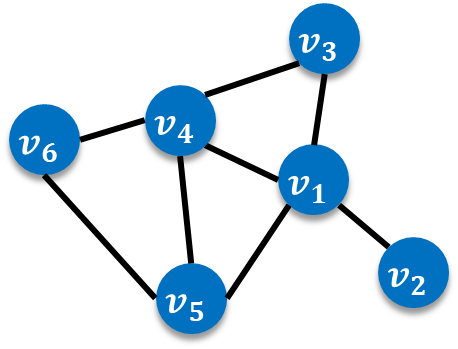
媒介中心性は，注目しているノードがそれ以外の2つのノード間の最短経路にどのくらいの割合で入っているかを数値にしたものです．注目しているノードをノード$v_i$とします．$v_i$を除いて選んだ2点（始点$v_s$と終点$v_t$）を結ぶ最短経路の中で$v_i$を通る度合いが$v_i$の媒介中心性$b_i$となります．具体的に以下のようなネットワークで媒介中心性を求めてみましょう．

ノード$v_4$の媒介中心性$b_4$を求めてみます．したがって，$v_4$を除いた2点の最短経路の中に$v_4$がどのくらい入っているかを調べていきます．

• $v_4$が最短経路に入る度合い
  • $v_1$から$v_2$の最短経路の中に$v_4$は入っていない（$v_1$と$v_2$は直接つながっている）：0
  • $v_1$から$v_3$の最短経路の中に$v_4$は入っていない（$v_1$と$v_3$は直接つながっている）：0
  • $v_1$から$v_5$の最短経路の中に$v_4$は入っていない（$v_1$と$v_5$は直接つながっている）：0
  • $v_1$から$v_6$の最短経路は2つ（$v_1 \to v_4 \to v_6$と$v_1 \to v_5 \to v_6$）うちの1つ（$v_1 \to v_4 \to v_6$）が$v_4$を通る：$\frac{1}{2}$
  • $v_2$から$v_3$の最短経路の中に$v_4$は入っていない（最短経路は$v_1$を通る1本のみ）：0
  • $v_2$から$v_5$の最短経路の中に$v_4$は入っていない（最短経路は$v_1$を通る1本のみ）：0
  • $v_2$から$v_6$の最短経路は2つ（$v_2 \to v_1 \to v_4 \to v_6$と$v_2 \to v_1 \to v_5 \to v_6$）のうち1つ（$v_2 \to v_1 \to v_4 \to v_6$）が$v_4$を通る：$\frac{1}{2}$
  • $v_3$から$v_5$の最短経路は2つ（$v_3 \to v_1 \to v_5$と$v_3 \to v_4 \to v_5$）のうち1つ（$v_3 \to v_4 \to v_5$）が$v_4$を通る：$\frac{1}{2}$
  • $v_3$から$v_6$の最短経路は$v_4$を通る1つ（$v_3 \to v_4 \to v_6$）のみ：1
  • $v_5$から$v_6$のに最短経路の中に$v_4$は入っていない（$v_5$と$v_6$は直接つながっている）：0

これの総和を取ると$\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+1=\frac{5}{2}$で，これが$v_4$が最短経路に入る度合いです．この値をさらにペアの総数（2つのノードで1つのペアができます）で割って規格化したものが$v_4$の媒介中心性$b_4$です．ペアの総数は上記箇条書きのように全部で10ペアありますが，これはノード数6個のうち，$v_4$の1つを除いた5個のノードから2つのノードを1つのペアとして取る組み合わせの数${}_5 C_2=10$通り（ペア）そのものです．したがって，$b_4$は

$$
b_4 = \frac{5/2}{10} = 0.25
$$

となります．同様にして各$b_i$を計算すると$b_1=0.45,, b_2=0,, b_3=0,, b_5=0.1,, b_6=0$となります．

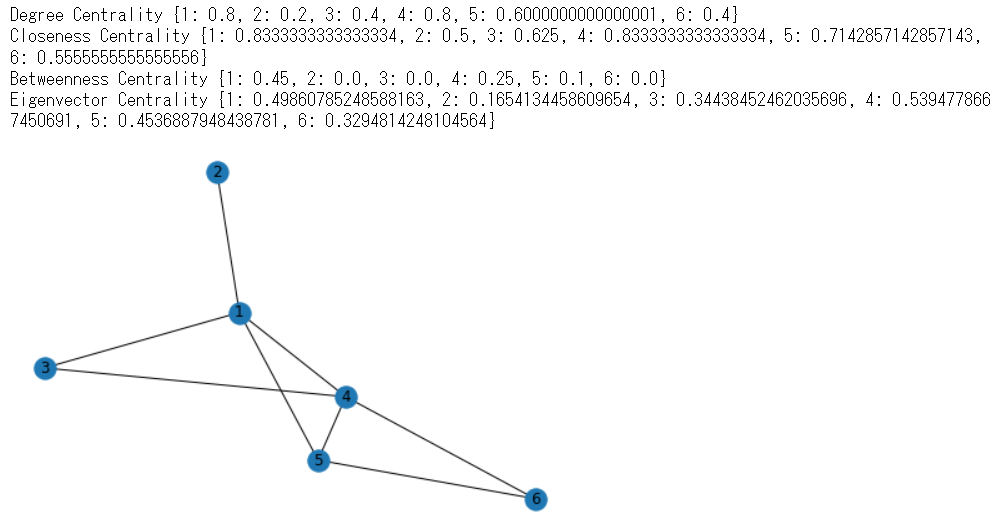
Pythonのネットワーク分析ツールであるNetworkXで上記ネットワークの各ノードの媒介中心性を求めてみましょう．具体的なコードは以下です．

コード

centrality

import networkx as nx  # NetworkXをインポート

# ネットワーク生成
G = nx.Graph([(1, 2), (1,3), (1,4), (1,5), (3, 4), (4,5), (4,6),(5,6)])
nx.draw(G, with_labels=True)  # ラベルをTrueにして番号の可視化
print('Degree Centrality', nx.degree_centrality(G))
print('Closeness Centrality', nx.closeness_centrality(G))
print('Betweenness Centrality', nx.betweenness_centrality(G))
print('Eigenvector Centrality', nx.eigenvector_centrality(G))

出力結果は以下のようになります．まず上記の図と同じネットワークをNetworkXで生成し，4つの中心性指標をまとめて出しています（次数中心性のbetweenness_centrality()と近接中心性のcloseness_centrality()は前回の記事で既に求めています）．NetworkXの組み込み関数betweenness_centrality()にネットワークのオブジェクトGを渡すことで各ノードの媒介中心性を求めてくれます．Betweenness Centralityの部分を見ると，Betweenness Centrality {1: 0.45, 2: 0.0, 3: 0.0, 4: 0.25, 5: 0.1, 6: 0.0}となっており，$b_1=0.45,, b_2=0,, b_3=0,, b_4=0.25, b_5=0.1,, b_6=0$に値がそれぞれ一致することが分かります．

結果

固有ベクトル中心性

固有ベクトル中心性は，中心的なノードとつながっているノードを中心的であるとみなす指標です（トートロジーのように聞こえますが）．人のネットワークであれば重要な人とつながっている人を重要と考えるということです．ノード$v_i$の中心性を$x_i$として，それを並べた$\boldsymbol{x}(t)=(x_1; x_2; \cdots; x_N)^T$を考えます．ここで$N$はノード数です．このベクトルには時刻$t$がついており，各ノードの中心性$x_i$は毎時間移動（変化）すると考えます．どのように移動するかというとリンクがつながっているところに移動していきます．ネットワークのノード間の繋がり方は隣接行列$A$で表せますので，$\boldsymbol{x}(t+1)=A\boldsymbol{x}(t)$という漸化式を考えて，$x_i$がどのように時間的に変化していくかを考えます．

では具体的に，前例と同じネットワークで考えてみましょう．このネットワークの繋がり方を表した$A$は

A=\begin{pmatrix}
0 & 1 & 1 & 1 & 1 & 0\\
1 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 1 & 0 & 0\\
1 & 0 & 1 & 0 & 1 & 1\\
1 & 0 & 0 & 1 & 0 & 1\\
0 & 0 & 0 & 1 & 1 & 0\\
\end{pmatrix}

となります．ノード同士がつながっている（リンクがある）なら1，そうでなければ0の値が入ります．例えば，$A$の1行目はノード$v_1$の繋がり方を示しています．$v_1$は$v_1$自身と$v_6$にはつながっていないので，その要素が0となり，その他の$v_2, v_3, v_4, v_5$とはつながっているので，その要素が1となります．他のノードの繋がり方についても同様です．

さて，時間$0$で各ノードが初期値として$\boldsymbol{x}(0)=(\frac{1}{6}; \frac{1}{6}; \frac{1}{6}; \frac{1}{6}; \frac{1}{6}; \frac{1}{6})$という中心性の値をそれぞれ持っていたとしましょう．次の時刻になるたびに，この中心性は$\boldsymbol{x}(t+1)=A\boldsymbol{x}(t)$の漸化式にしたがって移動します（ノード間にリンクがあれば移動する）ので，次の時刻$\boldsymbol{x}(1)$は，$\boldsymbol{x}(1)=A\boldsymbol{x}(0)$で求めることができます．これを手で計算するのは面倒くさいので，Pythonで求めてあげると

• $\boldsymbol{x}(1)=A\boldsymbol{x}(0)\approx(0.667; 0.167; 0.333; 0.667; 0.500; 0.333)^T$

となりました．このまま続けて漸化式を適用していくと，$x_i$の値が発散してしまうので，これを規格化してあげます（NetworkXではL2ノルムで規格化しているので，ここでもL2ノルムを使います）．$\boldsymbol{x}(1)$を規格化すると，

• $\boldsymbol{x}(1)\approx (0.566; 0.141; 0.283; 0.566; 0.424; 0.283)^T$

となります．さらに次の時刻での（規格化済みの）中心性は

• $\boldsymbol{x}(2)=A\boldsymbol{x}(1)\approx (0.471; 0.189; 0.377; 0.519; 0.471; 0.330)^T$

となります．この計算をさらに続けると，

• $\boldsymbol{x}(49)=(0.499; 0.165; 0.344; 0.539; 0.454; 0.329)^T$
• $\boldsymbol{x}(50)=(0.499; 0.165; 0.344; 0.539; 0.454; 0.329)^T$

のように各中心性$x_i$の値はある値に収束していきます．実際，横軸に時刻$t$，縦軸に中心性の値をとったグラフは以下のようになり，数ステップですぐに収束していることが分かります．

この収束した値が固有ベクトル中心性の値となります．つまり，収束したベクトル$\boldsymbol{x}$は$A\boldsymbol{x}=\lambda_1 \boldsymbol{x}$を満たす固有ベクトルということになります．ここで$\lambda_1$は$A$の最大固有値です．

初期値を変えても中心性の値は収束するのか確かめてみましょう．$\boldsymbol{x}(0)=(0.5; 0; 0; 0; 0; 0.5)^T$として始めてみます．再び$\boldsymbol{x}(t+1)=A\boldsymbol{x}(t)$を適用して中心性の値を移動させると

• $\boldsymbol{x}(1)=A\boldsymbol{x}(0)=(0; 0.316; 0.316; 0.632; 0.632; 0)^T$
• $\boldsymbol{x}(2)=A\boldsymbol{x}(1)=(0.722; 0; 0.241; 0.361; 0.241; 0.482)^T$
• $\ldots$
• $\boldsymbol{x}(49)=(0.499; 0.165; 0.344; 0.539; 0.454; 0.329)^T$
• $\boldsymbol{x}(50)=(0.499; 0.165; 0.344; 0.539; 0.454; 0.329)^T$

となり，やはりさきほどと同じところに収束します．この時の$x_i$の推移は以下のようになります．

ではこれもNetworkXの結果を見てみましょう．コードの中に既に書いてあるeigenvector_centrality(G)の部分です．NetworkXの組み込み関数eigenvector_centrality()にGを渡せばよいです．結果のEigenvector Centrality {1: 0.49860785248588163, 2: 0.1654134458609654, 3: 0.34438452462035696, 4: 0.5394778667450691, 5: 0.4536887948438781, 6: 0.3294814248104564}を見ると，上で計算した$\boldsymbol{x}=(0.499; 0.165; 0.344; 0.539; 0.454; 0.329)^T$と一致することが分かります．

動画解説

この記事の内容は私のチャンネルの以下の動画で解説していますので，よろしければ併せてご覧ください．もし今後とも役に立ちそうであればチャンネル登録もよろしくお願いします．