ネットワーク(グラフ)とは,以下のように**頂点(ノード)が辺(エッジ,リンク)**で結ばれたものです.
このようなネットワークにおいて中心的なノードを見つけたいことがあります.人のつながりをネットワークとして捉えるならば,中心的な人は,その文脈に依存して,友人が多い人,うわさを広めてしまう人,感染症を拡げてしまう人,他人に影響力がある人,…と解釈することができます.
ネットワークの中心的なノードを見つける時に,中心性という指標が使えます.中心性指標にもいくつかありますが,この記事では次数中心性,近接中心性の2つを説明します.媒介中心性,固有ベクトル中心性の2つについてはこちらの記事で説明しています.これまでに書いたネットワークの記事
も併せてご覧ください.
次数中心性
次数中心性は,各ノードが持つリンクの数(=次数)です.具体的に以下のようなネットワークで次数中心性を求めてみましょう.
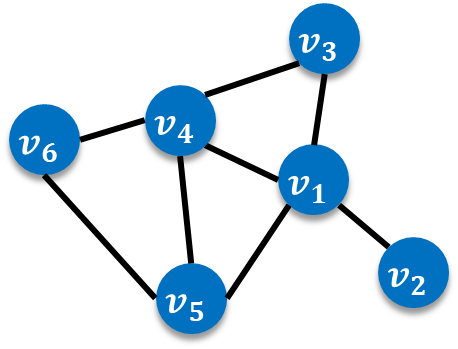
ノード$v_i$の次数$k_i$が$v_i$の次数中心性となります.すなわち上のネットワークでは,$k_1=4,, k_2=1,, k_3=2,, k_4=4,, k_5=3,, k_6=2$となります.
Pythonのネットワーク分析ツールであるNetworkXで上記ネットワークの各ノードの次数中心性を求めてみましょう.NetowrkXでは,次数中心性は上記$k_i$を$N-1$で割って,正規化したものが出力されます.$N$はノード数です.したがって,$k_1=\frac{4}{5}=0.8,, k_2=\frac{1}{5}=0.2,, k_3=\frac{2}{5}=0.4,, k_4=\frac{4}{5}=0.8,, k_5=\frac{3}{5}=0.6,, k_6=\frac{2}{5}=0.4$となります.具体的なコードは以下です.
コード
import networkx as nx # NetworkXをインポート
# ネットワーク生成
G = nx.Graph([(1, 2), (1,3), (1,4), (1,5), (3, 4), (4,5), (4,6),(5,6)])
nx.draw(G, with_labels=True) # ラベルをTrueにして番号の可視化
print('Degree Centrality', nx.degree_centrality(G))
print('Closeness Centrality', nx.closeness_centrality(G))
print('Betweenness Centrality', nx.betweenness_centrality(G))
print('Eigenvector Centrality', nx.eigenvector_centrality(G))
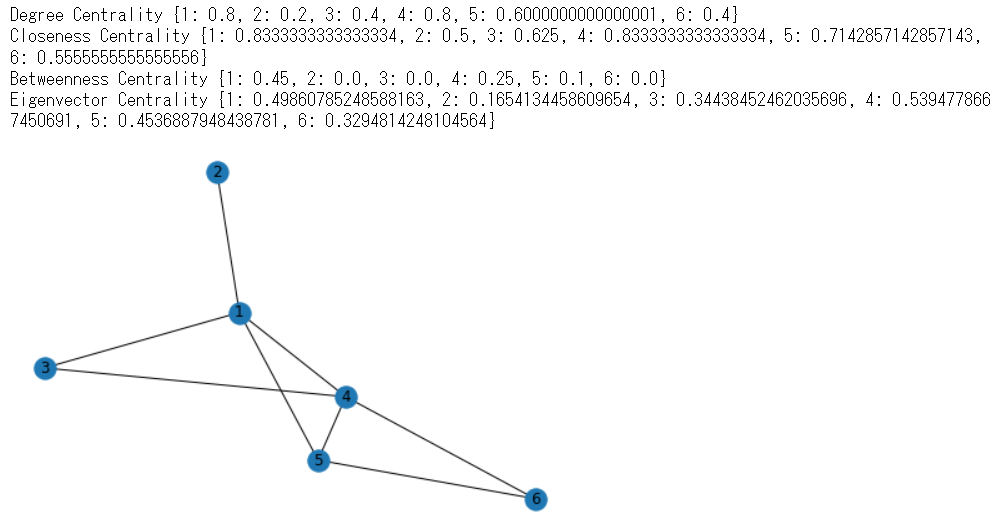
出力結果は以下のようになります.まず上記の図と同じネットワークをNetworkXで生成し,4つの中心性指標をまとめて出しています.NetworkXの組み込み関数degree_centrality()にネットワークのオブジェクトGを渡すことで各ノードの次数中心性を求めてくれます.Degree Centralityの部分を見ていただくと,Degree Centrality {1: 0.8, 2: 0.2, 3: 0.4, 4: 0.8, 5: 0.6000000000000001, 6: 0.4}となっており,$k_1=0.8,, k_2=0.2,, k_3=0.4,, k_4=0.8,, k_5=0.6,, k_6=0.4$に値がそれぞれ一致することが分かります.
結果
近接中心性
近接中心性は,あるノードから他の全てのノードへの距離(最短経路長)の平均値の逆数をとったものです.平均的な距離が小さいほど中心性の値は大きくなってほしいので,逆数をとります.式で書くと,ノード$v_i$の近接中心性は,
$$
l_i = \frac{\sum d_{ij}}{N-1}の逆数=\frac{N-1}{\sum d_{ij}}
$$
となります.具体的にまた前の例と同じネットワークで考えてみましょう.
まずノード$v_1$を始点として他の全てのノードへの距離(最短経路長)$d_{12},, d_{13},, d_{14},, d_{15},, d_{16}$を求めてみましょう.$v_1$と$v_2$,$v_1$と$v_3$,$v_1$と$v_4$,$v_1$と$v_5$は直接(リンク数は1つ)つながっているので$d_{12}=d_{13}=d_{14}=d_{15}=1$となります.$v_1$と$v_6$は間に2本のリンク($v_4$経由でも$v_5$経由でも良い)でつながっているので,$d_{16}=2$となります.したがって,ノード$v_1$の近接中心性$l_1$は,
$$
l_1 = \frac{N-1}{\sum d_{ij}}=\frac{5}{1+1+1+1+2}\approx0.83
$$
となります.同様に求めると,$l_2=0.5,, l_3=0.625,, l_4\approx0.83,, l_5\approx0.71,, l_6\approx0.56$となります.
ではこれもNetworkXの結果を見てみましょう.コードの中に既に書いてあるcloseness_centrality(G)の部分です.NetworkXの組み込み関数closeness_centrality()にGを渡せばよいです.結果のCloseness Centrality {1: 0.8333333333333334, 2: 0.5, 3: 0.625, 4: 0.8333333333333334, 5: 0.7142857142857143, 6: 0.5555555555555556}を見ると上で計算した$l_1, \ldots, l_6$と一致することが分かります.
動画解説
この記事の内容は私のチャンネルの以下の動画で解説していますので,よろしければ併せてご覧ください.もし今後とも役に立ちそうであればチャンネル登録もよろしくお願いします.