この記事はPython Advent Calendarの17日目の記事です。去年の記事で書かなかったPythonを使った音響信号処理関連の内容について書きます。
目次
- サンプリングレートを変換したい
- waveモジュールで24bitの音声ファイルを読みたい
- 群遅延をscipy.signal.group_delayで推定したい
- フレーム処理をnumpyのstrideトリックを使って行いたい(スペクトログラムを描画したい)
- TSP信号を生成したい
- 零点、極を可視化したい
サンプリングレートを変換したい
サンプリングレートを変換するためには、元のサンプリングレートと変換したいサンプリングレートが整数比であればアップ/ダウンサンプリングどちらか一方だけで済みますが、有理数比の場合はそれぞれのサンプリングレートの最小公倍数にアップサンプリングしてから、求めたいサンプリングレートにダウンサンプリングする必要があります。
ここではサンプリングレートを48kHzから44.1kHzに変換することを考えます。サンプリングレート変換は下記のようなコードで実現可能です。48kHzの音源の冒頭10秒を対象としています。
# !/usr/bin/env python
# vim:fileencoding=utf-8
from fractions import Fraction
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import scipy.signal as sg
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
fs_target = 44100
cutoff_hz = 21000.0
n_lpf = 4096
sec = 10
wav, fs_src = sf.read("../wav/souvenir_mono_16bit_48kHz.wav")
wav_48kHz = wav[:fs_src * sec]
frac = Fraction(fs_target, fs_src) # 44100 / 48000
up = frac.numerator # 147
down = frac.denominator # 160
# up sampling
wav_up = np.zeros(np.alen(wav_48kHz) * up)
wav_up[::up] = up * wav_48kHz
fs_up = fs_src * up
cutoff = cutoff_hz / (fs_up / 2.0)
lpf = sg.firwin(n_lpf, cutoff)
# filtering and down sampling
wav_down = sg.lfilter(lpf, [1], wav_up)[n_lpf // 2::down]
# write wave file
sf.write("down.wav", wav_down, fs_target)
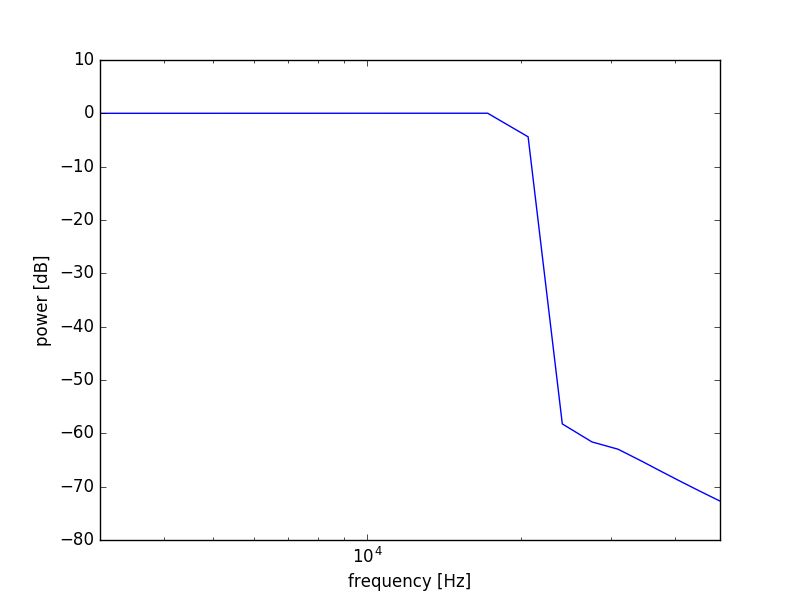
# lowpass filter plot
w, h = sg.freqz(lpf, a=1, worN=1024)
f = fs_up * w / (2.0 * np.pi)
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax.semilogx(f, 20.0 * np.log10(np.abs(h)))
ax.axvline(fs_target, color="r")
ax.set_ylim([-80.0, 10.0])
ax.set_xlim([3000.0, fs_target + 5000.0])
ax.set_xlabel("frequency [Hz]")
ax.set_ylabel("power [dB]")
plt.show()
44100/48000=147/160であるため、最初に元音源を147倍の点数にアップサンプリングします。ここでは147倍のサイズのバッファを作り、そのバッファに147点間隔で元信号を代入します。これにより代入されていない点についてはゼロ詰めがなされたことになります。次に、44100Hzのナイキスト周波数以下の周波数のみを含めるためにLPFを設計し、lfilterを使ってLPFを適用し帯域を制限します。ここでポイントとなるのが、アップサンプリング時のナイキスト周波数は48000/2=24000Hzですが、ダウンサンプリング後には44100/2=22050Hzがナイキスト周波数となるため、アップサンプリング時に適用する帯域制限フィルタは22050以下になるようなフィルタ一つで済むということが挙げられます。帯域制限を行った後は、LPFによる遅延を補正した上で今度は160点間隔でダウンサンプリングを行います。これによりサンプリングレート変換が実現できました。
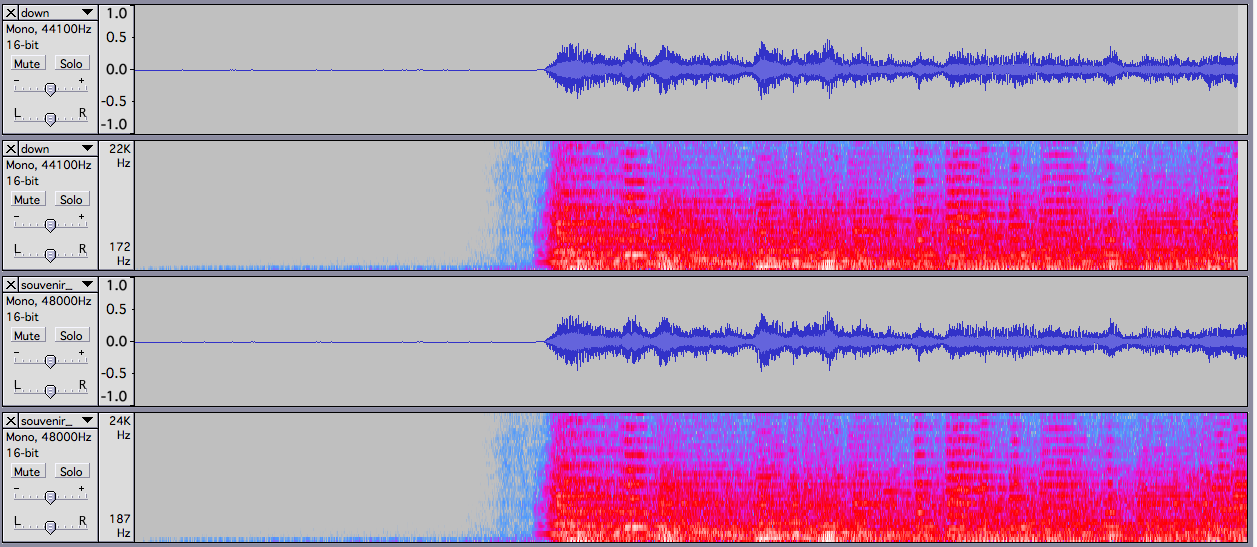
実際の音声波形とスペクトログラムは下記の通りです。上2つが44.1kHzの変換後、下2つが変換前です。
waveモジュールで24bitの音声ファイルを読みたい
標準のwaveモジュールで16bitの音声ファイルを読む場合はwave.openして必要な分だけreadframesで読み込みnp.frombufferでint16に変換すれば良いのですが、24bit音源の場合はfrombufferで24bitが指定できないため自力で読む必要があります。ここでは下記のコードのようにstructモジュールのunpackを用いて3byteずつ読み込みつつ、0を詰めてint32としてunpackすることで24bit音源の読み込みを実現しています。
ちなみに読み込んでいる音源はe-onkyoのサンプル音源を用いています。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import wave
from struct import unpack
if __name__ == '__main__':
plt.close("all")
fname = "../wav/souvenir.wav"
fp = wave.open(fname, "r")
nframe = fp.getnframes()
nchan = fp.getnchannels()
nbyte = fp.getsampwidth()
fs = fp.getframerate()
print("frame:{0}, "
"channel:{1}, "
"bytewidth:{2}, "
"fs:{3}".format(nframe, nchan, nbyte, fs))
buf = fp.readframes(nframe * nchan)
fp.close()
read_sec = 40
read_sample = read_sec * nchan * fs
print("read {0} second (= {1} frame)...".format(read_sec,
read_sample))
# 最下位bitに0を詰めてintにunpackすることで
# 24bitの値を32bit intとして値を取り出す
# (<iはリトルエンディアンのint値を仮定)
# unpackはtupleを返すので[0]を取る
unpacked_buf = [unpack("<i",
bytearray([0]) + buf[nbyte * i:nbyte * (i + 1)])[0]
for i in range(read_sample)]
# ndarray化
ndarr_buf = np.array(unpacked_buf)
# -1.0〜1.0に正規化
float_buf = np.where(ndarr_buf > 0,
ndarr_buf / (2.0 ** 31 - 1),
ndarr_buf / (2.0 ** 31))
# interleaveを解く(ステレオ音源の場合)
wav_l = float_buf[::2]
wav_r = float_buf[1::2]
time = np.arange(np.alen(wav_l)) / fs
# plot
fig = plt.figure(1)
ax = fig.add_subplot(2, 1, 1)
ax.plot(time, wav_l)
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax.set_title("left channel")
ax.grid()
ax = fig.add_subplot(2, 1, 2)
ax.plot(time, wav_r)
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax.set_title("right channel")
ax.grid()
plt.show()
群遅延をscipy.signal.groupdelayで推定したい
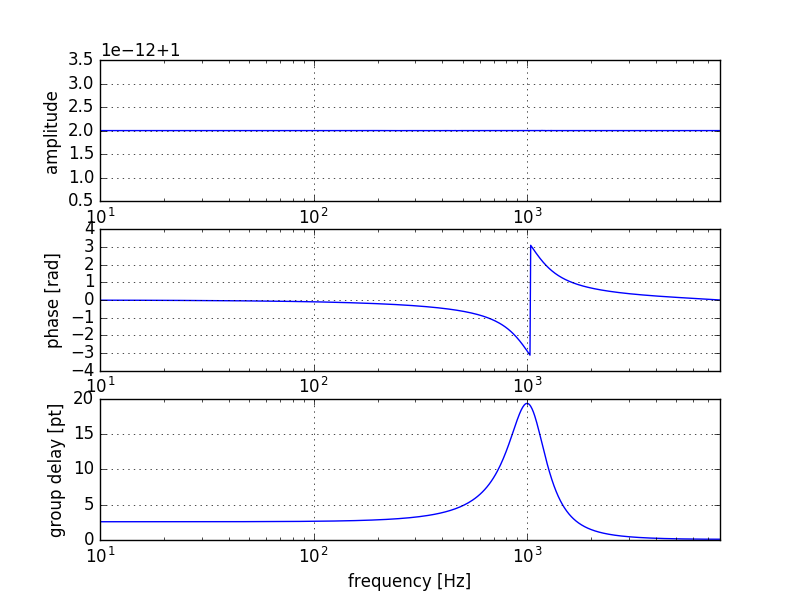
去年の記事のこの項目を書いた時には気付いてませんでしたが、群遅延を求めるためのgroup_delayメソッドがscipy.signalのバージョン0.16.0から追加されていました。これを用いてデジタルフィルタの群遅延を求めることができます。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sg
def allpass_filter(freq, r=0.9, fs=16000.0):
omega = 2.0 * np.pi * freq / fs
b = [r ** 2, - 2.0 * r * np.cos(omega), 1.0]
a = [1.0, -2.0 * r * np.cos(omega), r ** 2]
return (b, a)
if __name__ == '__main__':
plt.close("all")
fs = 16000.0
N = 1024
b, a = allpass_filter(1000.0)
w, h = sg.freqz(b, a, worN=N)
f = w * fs / (2.0 * np.pi)
_, gd = sg.group_delay((b, a), w=w)
fig = plt.figure(1)
ax = fig.add_subplot(3, 1, 1)
ax.semilogx(f, np.abs(h))
ax.grid()
ax.set_xlabel("frequency [Hz]")
ax.set_ylabel("amplitude")
ax.set_xlim([10.0, fs / 2.0])
ax = fig.add_subplot(3, 1, 2)
ax.semilogx(f, np.angle(h))
ax.grid()
ax.set_xlabel("frequency [Hz]")
ax.set_ylabel("phase [rad]")
ax.set_xlim([10.0, fs / 2.0])
ax = fig.add_subplot(3, 1, 3)
ax.semilogx(f, gd)
ax.grid()
ax.set_xlabel("frequency [Hz]")
ax.set_ylabel("group delay [pt]")
ax.set_xlim([10.0, fs / 2.0])
plt.show()
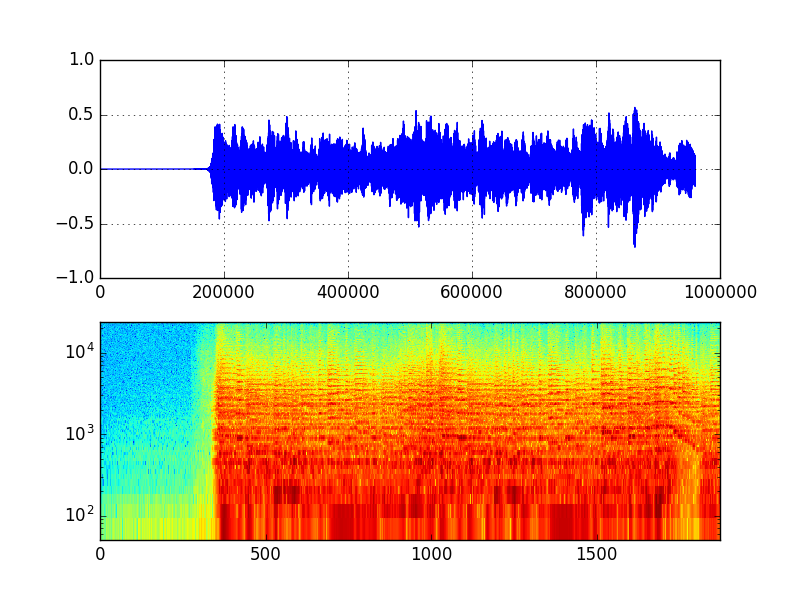
フレーム処理をnumpyのstrideトリックを使って行いたい(スペクトログラムを描画したい)
IPythonデータサイエンスクックブックのレシピ4.6や4.7でも紹介されているstrideトリックを用いると、一つのバッファを短時間フレームに区切って繰り返しアクセスするフレーム処理を、フレームのコピーを発生させずに効率良く行うことができます。
numpy.lib.stride_tricks下のas_stridedを用いるとスペクトログラムを計算するためのメソッドを下記のように書くことができます。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import scipy.fftpack as fft
from numpy.lib.stride_tricks import as_strided
import soundfile as sf
def spectrogram(xs, nfft=1024, noverlap=2, win=np.hanning):
nsample = np.alen(xs)
nframe = int(nsample * (noverlap / float(nfft))) - noverlap
nbyte = xs.dtype.itemsize
shift = (nfft // noverlap)
xs_split = as_strided(xs, (nframe, nfft), (nbyte * shift, nbyte))
window = win(nfft)
Xs = []
print(nsample, nframe, nfft, shift, nbyte, nfft * nframe)
for frame in xs_split:
Xs.append(20.0 * np.log10(np.abs(fft.fft(window * frame, nfft))[:nfft//2 + 1]))
return np.array(Xs)
if __name__ == '__main__':
plt.close("all")
wav, fs = sf.read("../wav/souvenir_mono_16bit_48kHz.wav")
sec = 20
nread = fs * sec
nfft = 1024
spec = spectrogram(wav[:nread], nfft=nfft, noverlap=2)
# plot
fig = plt.figure(1)
ax = fig.add_subplot(211)
ax.plot(wav[:nread])
ax.grid()
ax = fig.add_subplot(212)
ax.pcolor(np.arange(spec.shape[0]),
np.arange(nfft//2 + 1) * (fs / nfft),
spec.T,
cmap=cm.jet)
ax.set_xlim([0, spec.shape[0]])
ax.set_ylim([50, fs//2])
ax.set(yscale="log")
plt.show()
strideとは連続した領域にアクセスする際のバイト間隔を表す値です。これを変更すると、行や列のインデックスを一つ進めた際に何バイト先に進むかを制御することができるようになります。
as_stridedはこのstrideを疑似的に変更した状態でバッファにアクセスするためのメソッドです。第一引数はアクセス先のバッファ、第二引数はstride変更によって擬似的に作成されるバッファのshape、第三引数は変更したいstrideになります。第一引数のバッファを擬似的に第三引数のstrideに変更した上でアクセスすると、第二引数のshapeで示されるバッファとしてアクセスできるエイリアスを返す、といった具合の動作になります。
このstrideの形式は(行を進むときのバイト間隔, 列を進む時のバイト間隔)です。上記のスクリプトの場合、元の引数xsは1次元配列であり、そのstrideは(8,)となっているため、インデックスを1進めると8バイト(dtypeがfloat64)進むことになります。このstrideを例えばas_strideによって(512 * 8, 8)に変えると、本来1次元配列だったxsを2次元配列xs_splitとみなせるようになります。xs_splitにforループで繰り返しアクセスすると、アクセスの度にxs_splitの行方向に進む、つまりxsの512*8バイト先に進むため、xsを512ptずつずらしてアクセスできることになります。このように、本来であれば一次元配列を複数個の短時間フレームに切り出して処理していたようなフレーム処理を、strideトリックによって切り出し時のコピーを発生させずに行うことができるようになります。
注意としては、このstrideトリックを用いると容易に内部バッファの範囲外にアクセスできるようになってしまうため、ミスると未定義領域にアクセスして落ちることが多々発生します。
TSP信号を生成したい
音響測定時に用いるSweep Pulse(TSP信号)を設計する場合、周波数領域で設計したものをIFFTして時間領域に戻して得ることが多いかと思います。下記のようなコードで生成できます。N_expと実効長に寄与するm_expは要調整です。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack as fft
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
# parameters
N_exp = 16
m_exp = 2
nrepeat = 5
fs = 48000
gain = 100.0
N = 2 ** N_exp
m = N // (2 ** m_exp) # (J=2m)
a = ((m * np.pi) * (2.0 / N) ** 2)
tsp_freqs = np.zeros(N, dtype=np.complex128)
tsp_freqs[:(N // 2) + 1] = np.exp(-1j * a * (np.arange((N // 2) + 1) ** 2))
tsp_freqs[(N // 2) + 1:] = np.conj(tsp_freqs[1:(N // 2)][::-1])
# ifft and real
tsp = np.real(fft.ifft(tsp_freqs, N))
# roll
tsp = gain * np.roll(tsp, (N // 2) - m)
# repeat
tsp_repeat = np.r_[np.tile(tsp, nrepeat), np.zeros(N)]
# write
sf.write("tsp.wav", tsp_repeat, fs)
fig = plt.figure(1)
ax = fig.add_subplot(211)
ax.plot(tsp)
ax = fig.add_subplot(212)
ax.plot(tsp_repeat)
plt.show()
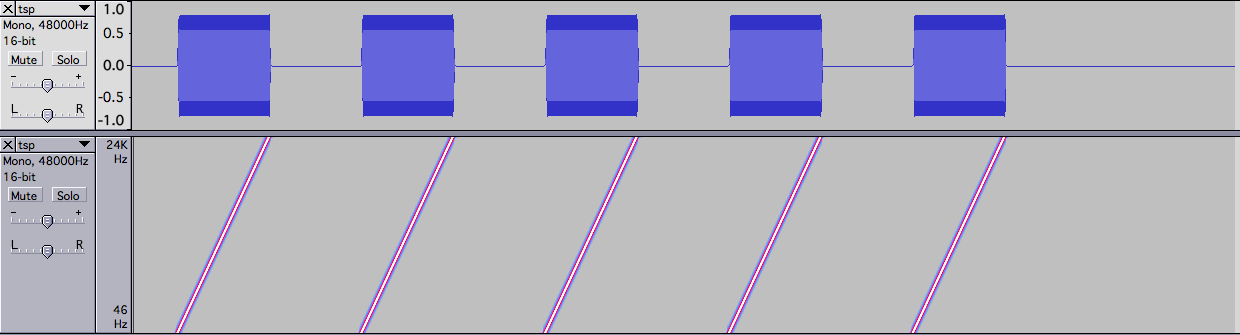
これにより生成されたwavファイルをaudacityで表示すると下記のようになります。
なおTSP信号については下記の金田先生のインパルス応答測定の基礎の講習資料に詳しく載っています。
http://www.asp.c.dendai.ac.jp/ASP/IRseminor2016.pdf
零点、極を可視化したい
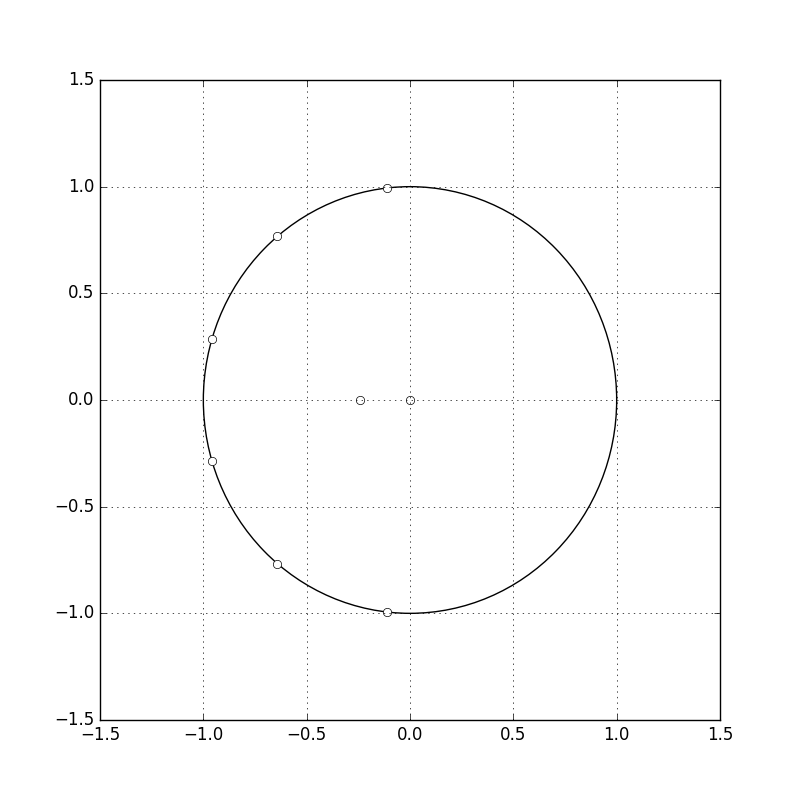
tf2zpkで時間フィルタ係数を零点、極に変換できますが、これを可視化するためには下記のようにadd_patchを使って円を書いた上で、線なし、マーカーありプロットをすると良い感じに書けます。図を貼ってから気付きましたがFIRフィルタなのでpoleがないですが無視して下さい。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import scipy.signal as sg
if __name__ == '__main__':
plt.close("all")
b = sg.firwin(11, 0.2, window="han")
z, p, k = sg.tf2zpk(b, [1])
fig = plt.figure(1, figsize=(8, 8))
ax = fig.add_subplot(111)
ax.add_patch(plt.Circle((0.0, 0.0), 1.0, fc="white"))
ax.plot(np.real(z), np.imag(z), "o", mfc="white")
ax.plot(np.real(p), np.imag(p), "x", mfc="white")
ax.grid()
ax.set_xlim([-1.5, 1.5])
ax.set_ylim([-1.5, 1.5])
plt.show()
その他
以下の内容についても書きたかったのですが時間が足りなかったため改めて追記するか別の記事で書きたいと思います。
- 入出力信号からインパルス応答を推定したい
- デジタルフィルタのSOS形式への変換
- ヒルベルト変換を用いて信号の包絡線を求めたい
ヒルベルト変換については下記のような説明文だけ書きましたのでとりあえず載せておきます。
信号の最大振幅を滑らかになぞる包絡線を求めるためには、絶対値や二乗値を取った信号に対しLPFを掛けて求める方法もありますが、ヒルベルト変換によって得られた解析信号から求める方法も知られています。
参考
https://jp.mathworks.com/help/dsp/examples/envelope-detection.html