1.はじめに
すごく今更ですが,Neural ODE実装ライブラリの使い方を紹介します.ちなみに,Neural ODE はNeurIPS 2018のbest paperに輝いた論文です.
このNeural ODE,著者らによってtorchdiffeqというライブラリ化された公式レポジトリが公開されています.
Neural ODEは理論や解釈を説明した記事は数多くあっても、このライブラリの実際の使い方を記述している日本語記事が少ないように思ったので、この記事で基礎的な使い方をまとめました.
ちなみにtorchdiffeqはPyTorch用のライブラリです.
この記事を読むことで、以下のことができるようになります.
- 一階常微分方程式の初期値問題をtorchdiffeqで解ける
- 二階常微分方程式の初期値問題をtorchdiffeqで解ける
- Neural ODEを構成する層であるODE Block層が実装できる
2.前提知識
torchdiffeqを使うに当たっての前提知識をおさらいします.
2.1 常微分方程式とは
微分方程式のうち,未知変数が本質的にただ一つのものを常微分方程式といいます.例えば,$\frac{dz}{dt}=f(z(t), t)$や,$m\ddot{x} = -kx$などの微分方程式は複数の変数が出てきますが,$z$や$x$は$t$の関数となるので,本質的に未知変数が$t$のただ一つしか存在せず,常微分方程式だと言えます.
2.2 Neural ODEとは
Neural ODEに関してはわかりやすい記事が他にたくさんあるので,そちらを参照していただきたいです.
一応,概要だけを簡単に説明すると,Neural ODEとは,「連続的な層をもつニューラルネットワーク」だと言えます.
「常微分方程式」というニューラルネット界隈では聞きなれない言葉があるせいでコンセプトが掴みにくくなっている説がありますが,重要な点は,「層を連続化した」したという点だと思っています.これにより従来のモデルでは不可能だった,例えば「0.5層目の出力を取り出す」といったことができるようになりました.
以下参考リンク:
3. torchdiffeqの使い方
それでは早速,torchdiffeqの使い方を見ていきましょう.
3.1 インストール
インストールするには以下のコマンドを実行します.
pip install torchdiffeq
3.2 例:一階微分方程式
実際にNeural ODEの実装に入る前に,簡単な一階常微分方程式を例にして,torchdiffeqの簡単な使い方を見ていきましょう.
以下の式微分方程式を考えます.
$$
z(0) = 0, \
\frac{dz(t)}{dt} = f(t) = t
$$
この解は$C$を積分定数として
$$
\int dz = \int tdt+C \
z(t) = \frac{t^2}{2} + C
$$
と書く下すことができ、$z(0) = 0$なので, この微分方程式の解は以下のようになることがわかります.
$$
z(t) = \frac{t^2}{2}
$$
torchdiffeqによる実装
この問題をtorchdiffeqで解くための最もシンプルな実装が以下になります.
from torchdiffeq import odeint
def func(t, z):
return t
z0 = torch.Tensor([0])
t = torch.linspace(0,2,100)
out = odeint(func, z0, t)
以下,ポイントを箇条書きにします.
-
関数
funcは上の微分方程式$\frac{dz}{dt}=f(t, z)$の$f$にあたります.引数は(t, z)の順番です.出力の次元はzに一致する必要があります.z,tのどちらかを用いなくても大丈夫です. -
変数
z0はダイナミクスの初期値になります. -
変数
tは時間を表し,tensor([0., 0.1, 0.2, ..., 0.9, 1.0])のように1次元テンソルである必要があります.t[0]は初期値に対応する時刻になります. -
注意すべきは,tの要素は狭義単調増加(減少)する列でなくてはならないということです.
t=tensor([0, 0, 1])のように,同じ値が含まれていてもエラーになります. -
odeint(func, z0, t)で微分方程式を解きます.引数は順番に関数func, 初期値y0,時刻tです. -
ソルバーは
tで指定されている時刻でのzの値を返します.つまり,t=tensor([t0, t1, ..., tn])のとき,out = tensor([z0, z1,..., zn])となります.t[0]は初期時刻なので,出力out[0]は必ずz0に一致しています.
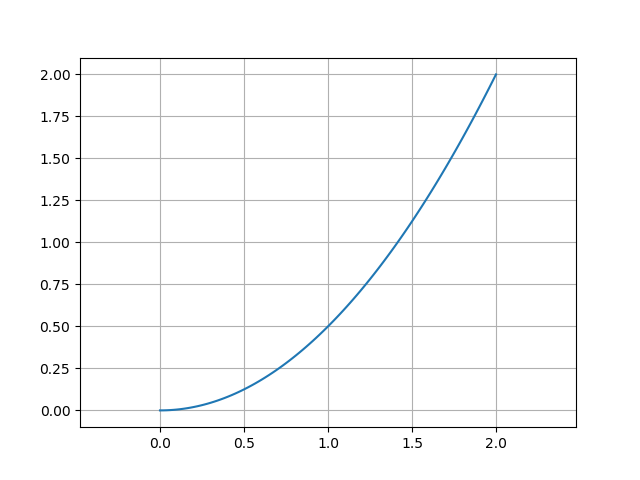
以上の結果をプロットします.
from matplotlib.pyplot as plt
plt.plot(t, out)
plt.axes().set_aspect('equal', 'datalim') # 縦横比を1:1にする
plt.grid()
plt.xlim(0,2)
plt.show()
手計算で求めた微分方程式の解$z = \frac{t^2}{2}$と一致していることがわかります.
3.3 (参考)例2:二階微分方程式を解く
torchdiffeqを使うと二階微分方程式も解けてしまいます.例として,理系には馴染み深い(?)単振動の微分方程式をtorchdiffeqで解きます.単振動の微分方程式は以下になります.
$$
m\ddot{x} = -kx
$$
初期状態として,$t=0$のとき,$x=1$, $\dot{x}=\frac{dx}{dt}=0$とします.
二階微分方程式を解くコツは,二階微分方程式を2つの一階微分方程式に分解することです.具体的には,以下のようにします.
$$
\left[
\begin{array}{c}
\dot{x} \\
\ddot{x} \
\end{array}
\right] =
\left[
\begin{array}{cc}
0 & 1\\
-\frac{k}{m} & 0\
\end{array}
\right]
\left[
\begin{array}{c}
x \
\dot{x} \
\end{array}
\right]
$$
ここで,$\boldsymbol{y}= \left[
\begin{array}{c}
x \
\dot{x} \
\end{array}
\right]$とおけば,この二階微分方程式は以下の一階微分方程式に帰着します.
$$
\frac{d\boldsymbol{y}}{dt} = f(\boldsymbol{y})
$$
実装は以下になります.$k=1, m=1$としています.
class Oscillation:
def __init__(self, km): # km = k/m
self.mat = torch.Tensor([[0, 1],
[-km, 0]])
def solve(self, t, x0, dx0):
y0 = torch.cat([x0, dx0])
out = odeint(self.func, y0, t)
return out
def func(self, t, y):
# print(t)
out = y @ self.mat # @は行列積
return out
if __name__=="__main__":
x0 = torch.Tensor([1])
dx0 = torch.Tensor([0])
import numpy as np
t = torch.linspace(0, 4 * np.pi, 1000)
solver = Oscillation(1)
out = solver.solve(t, x0, dx0)
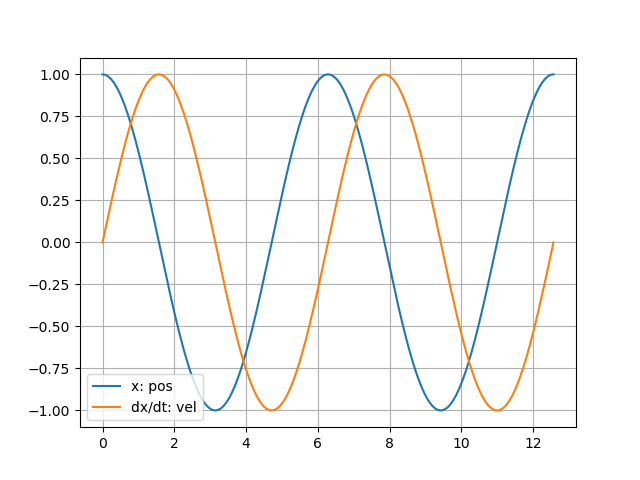
描画すると,きちんと単振動の解が求まっていることがわかります.
4.ODE Blockの実装
torchdiffeqの使い方に慣れてきたところで,実際のODE Blockの実装の仕方について見ていきましょう.ODE Blockとは,$\frac{dz}{dt} = f(t, z)$のダイナミクスを形成する一つのモジュールです.実際のNeural ODEは,通常のFull-Connect層や畳み込み層と共にODE Blockが使われて構成されています.
以下の実装は簡潔さを重視したものであり,あくまで一例です.
from torchdiffeq import odeint_adjoint as odeint
class ODEfunc(nn.Module):
def __init__(self, dim):
super(ODEfunc, self).__init__()
self.seq = nn.Sequential(nn.Linear(dim, 124),
nn.ReLU(),
nn.Linear(124, 124),
nn.ReLU(),
nn.Linear(124, dim),
nn.Tanh())
def forward(self, t, x):
out = self.seq(x)
return out
class ODEBlock(nn.Module):
def __init__(self, odefunc):
super(ODEBlock, self).__init__()
self.odefunc = odefunc
self.integration_time = torch.tensor([0, 1]).float()
def forward(self, x):
self.integration_time = self.integration_time.type_as(x)
out = odeint(self.odefunc, x, self.integration_time)
return out[1] # out[0]には初期値が入っているので.
簡単に解説をすると,
- ODE Blockは受け取った入力
xを微分方程式の初期値として扱います. -
ODEfuncが系のダイナミクスを記述する$f$となっています. - ODE Blockの積分区間は0~1で固定となっています.そして$t=1$での層の出力を返します.
こうすることで,以下のように,ニューラルネットの一つのモジュールとしてODE Blockを使うことができます.
class ODEnet(nn.Module):
def __init__(self, in_dim, mid_dim, out_dim):
super(ODEnet, self).__init__()
odefunc = ODEfunc(dim=mid_dim)
self.fc1 = nn.Linear(in_dim, mid_dim)
self.relu1 = nn.ReLU(inplace=True)
self.norm1 = nn.BatchNorm1d(mid_dim)
self.ode_block = ODEBlock(odefunc) # ODE Blockを使用
self.norm2 = nn.BatchNorm1d(mid_dim)
self.fc2 = nn.Linear(mid_dim, out_dim)
def forward(self, x):
batch_size = x.shape[0]
x = x.view(batch_size, -1)
out = self.fc1(x)
out = self.relu1(out)
out = self.norm1(out)
out = self.ode_block(out)
out = self.norm2(out)
out = self.fc2(out)
return out
このモデルは計算速度が遅かったです.
しかし,torchdiffeqを使えば必ず遅くなるわけでもないようで,自分が試した限りでは公式レポジトリのNeural ODEモデルでは通常のニューラルネットワークと遜色ない速度が出ていました.(こっちのほうがモデル小さいはずなのに...)
5. まとめ
Neural ODEの実装に役立つtorchdiffeqの初歩的な使い方を紹介しました.実際にモデルを訓練しているプログラムを見たい方は,以下のtorchdiffeqの公式レポジトリか筆者の実装レポジトリを参照してください.