Juliaの凸最適化のパッケージConvexとソルバーのラッパーのパッケージSCSでポートフォリオ最適化を試してみます。
ポートフォリオ最適化の説明やPythonとの比較は以前書いた記事を参考に。
- Scipyで２次計画問題を解く〜ポートフォリオ最適化の例〜
- CVXOPTで２次計画問題を解く〜ポートフォリオ最適化の例〜
- PyPortfolioOptでポートフォリオ最適化
この記事は以下を参考にしています。
https://jump.dev/Convex.jl/v0.12/examples/portfolio_optimization/portfolio_optimization2/
準備
パッケージをインストールする
パッケージの追加モードで以下のコマンドを実行します。
add Convex
add SCS
リスクとリターン
パッケージをインポートします。
using Convex, SCS
using Plots
リスクと期待リターンは、今回は実際のデータからではなく、仮の値を用います。
期待リターンμを
μ = [11.5; 9.5; 6] / 100
とします。なお、ギリシャ文字μは「\mu」と入力後「Tab」で変換できます。
次に、分散共分散行列Σを
Σ = [166 34 58
34 64 4
58 4 100] / 100^2
とします。投資対象資産数は
n = length(μ)
です。
ポートフォリオ最適化
二次計画問題を解く
目的関数
$$\lambda \times risk − (1 − \lambda ) \times return$$
を最小化する問題を解きます。
効率的フロンティアを作成するため、λを複数パターン用意します。
N = 101
λ_vals = range(0.01, stop=0.99, length=N)
ConvexのVariableで決定変数を作成します。
w = Variable(n)
ポートフォリオのリターンは
ret = dot(w, μ)
です。ポートフォリオのリスクは
risk = quadform(w, Σ)
です。 数理計画問題を、minimizeの1つ目の引数に目的関数、2つ目の引数に制約条件を入れて、定義します。
λ = 0.5
problem = minimize(λ * risk - (1 - λ) * ret, sum(w) == 1)
以下のように返ります。
minimize
└─ + (convex; real)
├─ * (convex; positive)
│ ├─ 0.5
│ └─ * (convex; positive)
│ ├─ …
│ └─ …
└─ - (affine; real)
└─ * (affine; real)
├─ …
└─ …
subject to
└─ == constraint (affine)
├─ sum (affine; real)
│ └─ 3-element real variable (id: 144…983)
└─ 1
status: `solve!` not called yet
ソルバーにSCS.Optimizerを指定して実行します。
solve!(problem, SCS.Optimizer)
実行結果が表示されます。
----------------------------------------------------------------------------
SCS v2.1.4 - Splitting Conic Solver
(c) Brendan O'Donoghue, Stanford University, 2012
----------------------------------------------------------------------------
Lin-sys: sparse-indirect, nnz in A = 21, CG tol ~ 1/iter^(2.00)
eps = 1.00e-05, alpha = 1.50, max_iters = 5000, normalize = 1, scale = 1.00
acceleration_lookback = 10, rho_x = 1.00e-03
Variables n = 6, constraints m = 10
Cones: primal zero / dual free vars: 2
linear vars: 1
soc vars: 7, soc blks: 2
Setup time: 9.30e-05s
----------------------------------------------------------------------------
Iter | pri res | dua res | rel gap | pri obj | dua obj | kap/tau | time (s)
----------------------------------------------------------------------------
0| 1.83e+19 1.94e+19 1.00e+00 -3.24e+19 2.99e+18 3.81e+19 3.30e-05
79| 3.50e-11 5.84e-11 3.16e-11 -6.43e-02 -6.43e-02 2.26e-16 4.48e-04
----------------------------------------------------------------------------
Status: Solved
Timing: Solve time: 4.49e-04s
Lin-sys: avg # CG iterations: 3.30, avg solve time: 6.40e-07s
Cones: avg projection time: 7.48e-08s
Acceleration: avg step time: 3.97e-06s
----------------------------------------------------------------------------
Error metrics:
dist(s, K) = 1.1102e-16, dist(y, K*) = 2.7756e-17, s'y/|s||y| = -3.3910e-18
primal res: |Ax + s - b|_2 / (1 + |b|_2) = 3.5044e-11
dual res: |A'y + c|_2 / (1 + |c|_2) = 5.8361e-11
rel gap: |c'x + b'y| / (1 + |c'x| + |b'y|) = 3.1561e-11
----------------------------------------------------------------------------
c'x = -0.0643, -b'y = -0.0643
============================================================================
最適解は
evaluate(w)
3-element Vector{Float64}:
1.6436100090749952
0.978590254896493
-1.6222002640539048
で、そのときの期待リターンは
evaluate(ret)
0.18464920941555704
リスクは
evaluate(risk)
0.05602697621995912
です。
効率的フロンティア
効率的フロンティアをプロットするため、リスクとリターンの組み合わせを格納する箱を用意します。
MeanVarA = zeros(N, 2)
λを複数パターンで実行します。
for i = 1:N
λ = λ_vals[i]
problem = minimize(λ * risk - (1 - λ) * ret, sum(w) == 1)
solve!(problem, SCS.Optimizer)
MeanVarA[i,:]= [evaluate(ret),evaluate(risk)[1]]
end
決定変数に上下限制約を付ける場合です。
w_lower = 0
w_upper = 1
λ = 0.5
制約条件は第2引数以降で並べて書きます。
problem = minimize(λ * risk - (1 - λ) * ret,
sum(w) == 1,
w_lower <= w,
w <= w_upper)
solve!(problem, SCS.Optimizer)
最適解は
evaluate(w)
効率的フロンティアを描くため、複数のλのパターンで実行します。
MeanVarB = zeros(N, 2)
for i = 1:N
λ = λ_vals[i]
problem = minimize(λ * risk - (1 - λ) * ret,
sum(w) == 1,
w_lower <= w,
w <= w_upper)
solve!(problem, SCS.Optimizer)
MeanVarB[i,:]= [evaluate(ret), evaluate(risk)[1]]
end
効率的フロンティアをプロットします。
plot(sqrt.(MeanVarA[:,2]),
MeanVarA[:,1],
xlim = (0,0.25),
ylim = (0,0.15),
title = "Markowitz Efficient Frontier",
xlabel = "Standard deviation",
ylabel = "Expected return",
label = "no bounds on w")
plot!(sqrt.(MeanVarB[:,2]),
MeanVarB[:,1],
label = "with 0<w<1")
scatter!(sqrt.(diag(Σ)),μ,color=:red,label = "assets")
期待リターンが目標リターン以上となる制約条件を設定する場合のコードです。
まず目標リターンを複数パターン設定します。
retG_vals = range(minimum(μ),stop=maximum(μ),length=N)
実行します。
MeanVarC = zeros(N, 2)
for i = 1:N
retG = retG_vals[i]
problem = minimize(risk,
sum(w) == 1,
retG <= ret,
w_lower <= w,
w <= w_upper)
solve!(problem, SCS.Optimizer)
MeanVarC[i,:]= [evaluate(ret), evaluate(risk)[1]]
end
効率的フロンティアを描きます。
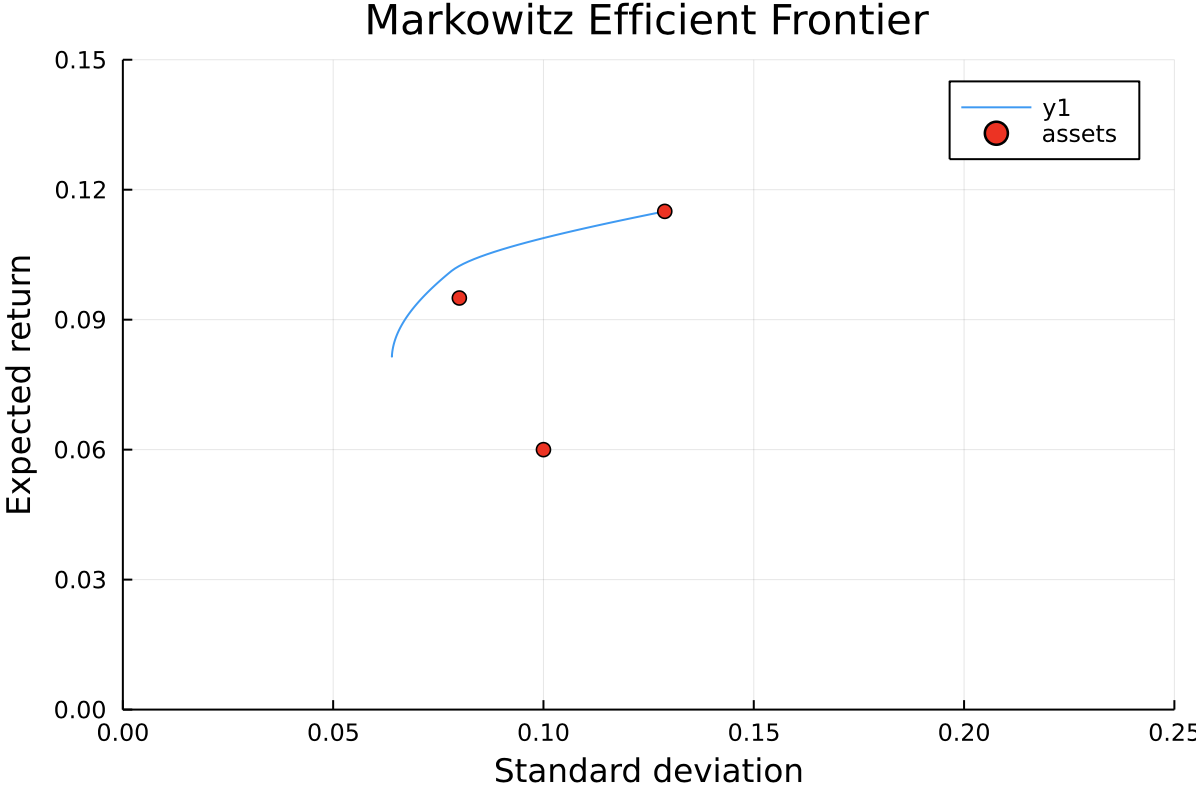
plot(sqrt.(MeanVarC[:,2]),
MeanVarC[:,1],
xlim = (0,0.25),
ylim = (0,0.15),
title = "Markowitz Efficient Frontier",
xlabel = "Standard deviation",
ylabel = "Expected return",
label = "Expected return >= Goal return")
scatter!(sqrt.(diag(Σ)),μ,color=:red,label = "assets")
おわり
PythonのScipyやCVXOPTと比べても、Juliaだと数式のように直感的に書けます。