PyPortfolioOptでポートフォリオ最適化
PyPortfolioOptという名前の通りポートフォリオ最適化のライブラリを教えてもらったので試してみました。
インストールはpipで問題なくできます。
時系列データの準備
import quandl
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
quandlで時系列データを取得します。
codes = ['WIKI/GOOG', 'WIKI/AAPL', 'WIKI/FB', 'WIKI/AMZN']
start = datetime(2017, 12, 1)
end = datetime(2017, 12, 31)
data = quandl.get(codes, start_date=start, end_date=end)
df = data[['WIKI/GOOG - Adj. Close', 'WIKI/AAPL - Adj. Close', 'WIKI/FB - Adj. Close', 'WIKI/AMZN - Adj. Close']]
df.columns = ['GOOG', 'AAPL', 'FB', 'AMZN']
期待リターンとリスク
from pypfopt import expected_returns
from pypfopt import risk_models
期待リターン
期待リターンには2つのメソッドが用意されているようです。
- mean_historical_return: 過去のリターンの平均
- ema_historical_return: 過去のリターンの指数加重平均
mean_historical_returnは過去のリターンの平均です。
expected_returns.mean_historical_return(df, frequency=252)
GOOG 0.474670
AAPL -0.130555
FB 0.116304
AMZN 0.090356
dtype: float64
mean_historical_returnは以下の計算と同じです。
df.pct_change().dropna(how='all').mean() * 252
GOOG 0.474670
AAPL -0.130555
FB 0.116304
AMZN 0.090356
dtype: float64
ema_historical_returnは過去のリターンの指数加重平均です。
expected_returns.ema_historical_return(df, frequency=252, span=500)
GOOG 0.458793
AAPL -0.141455
FB 0.106273
AMZN 0.087484
Name: 2017-12-29 00:00:00, dtype: float64
ema_historical_returnは以下の計算と同じです。
df.pct_change().dropna(how='all').ewm(span=500).mean().iloc[-1] * 252
GOOG 0.458793
AAPL -0.141455
FB 0.106273
AMZN 0.087484
Name: 2017-12-29 00:00:00, dtype: float64
リスク
リスクモデルはいくつか種類があるようです。
- sample_cov: 標本共分散
- semicovariance: 下方半分散
- exp_cov: 指数加重共分散
- min_cov_determinant: 最小共分散行列式
- CovarianceShrinkage: 共分散縮小推定
sample_covは標本分散共分散行列です。
risk_models.sample_cov(df, frequency=252)
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.014571 | 0.008801 | 0.014461 | 0.011802 |
| AAPL | 0.008801 | 0.023756 | 0.010244 | 0.006658 |
| FB | 0.014461 | 0.010244 | 0.028917 | 0.016893 |
| AMZN | 0.011802 | 0.006658 | 0.016893 | 0.019590 |
sample_covは以下の計算と同じです。
df.pct_change().dropna(how='all').cov() * 252
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.014571 | 0.008801 | 0.014461 | 0.011802 |
| AAPL | 0.008801 | 0.023756 | 0.010244 | 0.006658 |
| FB | 0.014461 | 0.010244 | 0.028917 | 0.016893 |
| AMZN | 0.011802 | 0.006658 | 0.016893 | 0.019590 |
semicovarianceは下方半分散です。分散と異なり、価格下落のみ考慮します。
risk_models.semicovariance(df, benchmark=0, frequency=252)
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.002546 | 0.001575 | 0.003063 | 0.003533 |
| AAPL | 0.001575 | 0.010416 | 0.004356 | 0.002411 |
| FB | 0.003063 | 0.004356 | 0.008031 | 0.007401 |
| AMZN | 0.003533 | 0.002411 | 0.007401 | 0.010043 |
exp_covは指数加重分散共分散行列です。
risk_models.exp_cov(df, span=180, frequency=252)
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.013511 | 0.008378 | 0.012941 | 0.010599 |
| AAPL | 0.008378 | 0.022943 | 0.009799 | 0.006117 |
| FB | 0.012941 | 0.009799 | 0.026141 | 0.015202 |
| AMZN | 0.010599 | 0.006117 | 0.015202 | 0.017994 |
最小共分散行列式と共分散縮小推定は…よくわかってません。。。(勉強したら、加筆します)
risk_models.min_cov_determinant(df, frequency=252, random_state=None)
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.008924 | 0.000422 | 0.011945 | 0.008615 |
| AAPL | 0.000422 | 0.004111 | 0.003965 | 0.003155 |
| FB | 0.011945 | 0.003965 | 0.027437 | 0.012774 |
| AMZN | 0.008615 | 0.003155 | 0.012774 | 0.012110 |
cs = risk_models.CovarianceShrinkage(df, frequency=252)
cs.ledoit_wolf()
| GOOG | AAPL | FB | AMZN | |
|---|---|---|---|---|
| GOOG | 0.015861 | 0.005803 | 0.009534 | 0.007781 |
| AAPL | 0.005803 | 0.021916 | 0.006753 | 0.004390 |
| FB | 0.009534 | 0.006753 | 0.025319 | 0.011138 |
| AMZN | 0.007781 | 0.004390 | 0.011138 | 0.019169 |
ポートフォリオ最適化
期待リターンとリスクはとりあえず標本平均、標本分散を用いることにします。
mu = expected_returns.mean_historical_return(df)
S = risk_models.sample_cov(df)
基本的なポートフォリオ最適化のメソッドには以下のものがあります。
- efficient_return: 分散最小化(目標リターン制約あり)
- min_volatility: 最小分散ポートフォリオ
- max_sharpe: シャープ・レシオ最大化
各メソッドは投資比率が返り値となります。なお、デフォルトでは空売り禁止制約があります。最適化にはscipy.optimizeのSLSQPを使っているようです。
from pypfopt.efficient_frontier import EfficientFrontier
ef = EfficientFrontier(mu, S)
分散最小化
ポートフォリオの期待リターンが目標リターン以上となる制約のもとポートフォリオの分散を最小化する基本的なモデルです。efficient_returnメソッドでは、目標リターンは正である必要があります。
ef.efficient_return(target_return=0.1)
{'AAPL': 0.3784758815412178,
'AMZN': 0.3788755190633175,
'FB': 2.168404344971009e-18,
'GOOG': 0.2426485993954646}
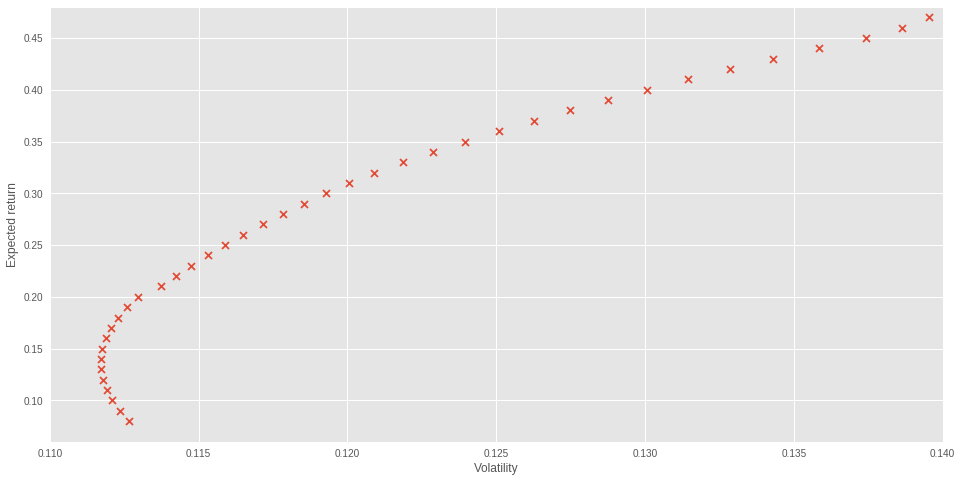
効率的フロンティア
効率的フロンティアをプロットします。
trets = np.arange(0.08, 0.48, 0.01)
tvols = []
for tr in trets:
w = ef.efficient_return(target_return=tr)
w = pd.Series(w).values
v = np.sqrt(np.dot(w.T, np.dot(np.array(S), w)))
tvols += [v]
plt.style.use('ggplot')
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(1, 1, 1)
ax.scatter(tvols, trets, marker='x')
ax.set_xlim([0.11, 0.14])
ax.set_ylim([0.06, 0.48])
ax.set_xlabel('Volatility')
ax.set_ylabel('Expected return')
ax.grid(True)
plt.show()
最小分散ポートフォリオ
目標リターンの制約がない分散最小化モデルです。
ef.min_volatility()
{'AAPL': 0.27828638691271423,
'AMZN': 0.2997733541261708,
'FB': 4.683753385137379e-17,
'GOOG': 0.4219402589611148}
シャープ・レシオ最大化
ポートフォリオのリターンを$r_p$、標準偏差を$\sigma_p$、リスクフリーレートを$r_f$としたとき、シャープ・レシオは
$$SR=\frac{r_p-r_f}{\sigma_p}$$
となります。リスクフリーレートは引数で指定します。
ef.max_sharpe(risk_free_rate=0.02)
{'AAPL': 3.469446951953614e-15,
'AMZN': 0.0,
'FB': 2.7755575615628914e-17,
'GOOG': 0.9999999999999971}
空売りを許す場合
引数のweight_boundsで空売り制約を調整できます。
ef = EfficientFrontier(mu, S, weight_bounds=(-1, 1))
ef.efficient_return(target_return=0.1)
{'AAPL': 0.3943771761924584,
'AMZN': 0.4342707677358275,
'FB': -0.08626091354681668,
'GOOG': 0.2576129696185309}
CVaR計算
CVaR(Conditional Value at Risk)は、ポートフォリオのリターンの損失がある確率水準を上回るときの期待損失のことです。(参考: Portfolio Value at Risk and Conditional Value at Risk)
from pypfopt.objective_functions import negative_cvar
適当な投資比率のときのCVaRを計算します。
weights = [0.25, 0.25, 0.25, 0.25]
negative_cvar(weights=weights, returns=df.pct_change().dropna(how='all'), s=10000, beta=0.95, random_state=None)
0.013806171739498746
CVaR最小化
基本的なポートフォリオ最適化のメソッドとは別にCVaR最小化のメソッドがあります。線形計画法ではなく、noisyoptというライブラリでSPSA(同時摂動確率近似)という手法を使って求めているようです。ただデフォルトのサンプル数$s=10000$では、解が安定しません。
from pypfopt.value_at_risk import CVAROpt
cvaropt = CVAROpt(df, weight_bounds=(0, 1))
cvaropt.min_cvar(s=10000, beta=0.95, random_state=None)
まとめ
- 1行で最適化のコードが書けるので、細かい制約条件など考えないのであれば手軽で便利です。
- リスク尺度が豊富です。
- そのうち他のライブラリとの比較もしたいと思います。
免責とか
本内容について、責任は負いません。もし内容に間違いがあれば修正しますのでコメントいただけるとありがたいです。
参考
以前、ポートフォリオ最適化について書きました。