目的
カルマンフィルタの性能をしっかりと引き出すために,フィルタの設計方法を知る必要があります。ここではカルマンフィルタを動作原理を理解するために必要な知識を紹介し,1からプログラムを組んで行こうと思います。可読性のために普段使用しないpythonでコードを書いたので,変な記述があったらすいません。
カルマンフィルタ
センサ信号の雑音を除去したいとなると思いつくのがこのフィルタだと思います。カルマンフィルタの行なっていることは
(1) 予測する
(2) 実信号を観測する
(3) 予測信号と観測信号を比べて,予測精度と観測精度を考慮して混ぜ合わせる
といったことをしています。ということは,
(1) 予測のためにモデルを作る
(2) 混ぜ率を考える
というステップが必要になります。学術的な言葉に置き換えると,モデルを用いて予測を行うことはオブザーバを設計すること,混ぜ率を考えることはカルマンゲインを決定することに相当します。
カルマンフィルタの使い道
カルマンフィルタがなぜ必要かというと,センサ信号は真値を含むが雑音が多い,しかしモデルを用いた予測は雑音の少ない推定ができるがモデルの誤差や入力の不確かさによって真値がわからない,そこで両者の良いところをとって真値を推定しようということです。
簡単な例を用いて説明します。直動モータが硬い壁に粘性,ばねを介して繋がれた慣性に作用するとします。推力を制御することができて,モータの位置を位置センサが取得できるとします。
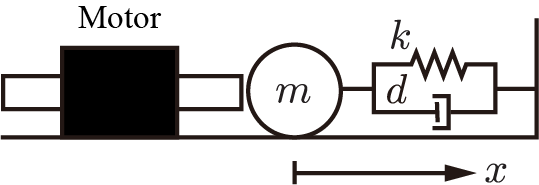
この時,モータ推力のリプルはシステムの入力として作用し,位置の変動を起こします。そして,位置センサの誤差は真値からの誤差です。予測は入力雑音の真値に対する影響がわからないため,真値がわかりません。ここで,観測雑音だけみても,これがセンサ由来の誤差なのか,それとも入力雑音由来の実際の位置変動なのかを見分けることができません。
記事の目的
今回は,簡単なシステムを用いてモデル化を行い,オブザーバを作ります。つまり,予測ステップを実装するところまで進めます。ここでは上の対象の位置の真値を求める問題を取り扱います。
シミュレータとデータセットの作成
上のシステムのシミュレータを作成し,推力指令値と位置応答値のデータセットを作成します。
import numpy as np
import math
# Time
time=0.0
time_sampling=1e-4
# Motion
position=0
velocity=0
acceleration=0
force=0
# For Integration with Tustin Transformation
velocity_z1=0
acceleration_z1=0
# Environment
env_k=3400
env_d=2.35
env_m=1.3
# Input and Sensor
force_ref=0
position_get=0
# simulator
sim_loop=100
# make data set
f=open("result.txt","w")
while time <= 30:
force_ref=3.0 if time>0.1 else 0.0
force=force_ref
for i in range(sim_loop):
#Position
position+=(velocity+velocity_z1)*time_sampling/sim_loop/2.0
velocity_z1=velocity
#Velocity
velocity+=(acceleration+acceleration_z1)*time_sampling/sim_loop/2.0
acceleration_z1=acceleration
#Acceleration
acceleration=(-env_k*position-velocity*env_d+force)/env_m
position_get=position
result = "{:.7f} {:.7f} {:.7f}\n".format(time, force_ref,position_get)
f.write(result)
time+=time_sampling
f.close()
このシミュレータでは開始から0.1秒後に3.0Nのモータ推力を発生させ,30秒間の応答を確認します。位置応答は次のようになりました。
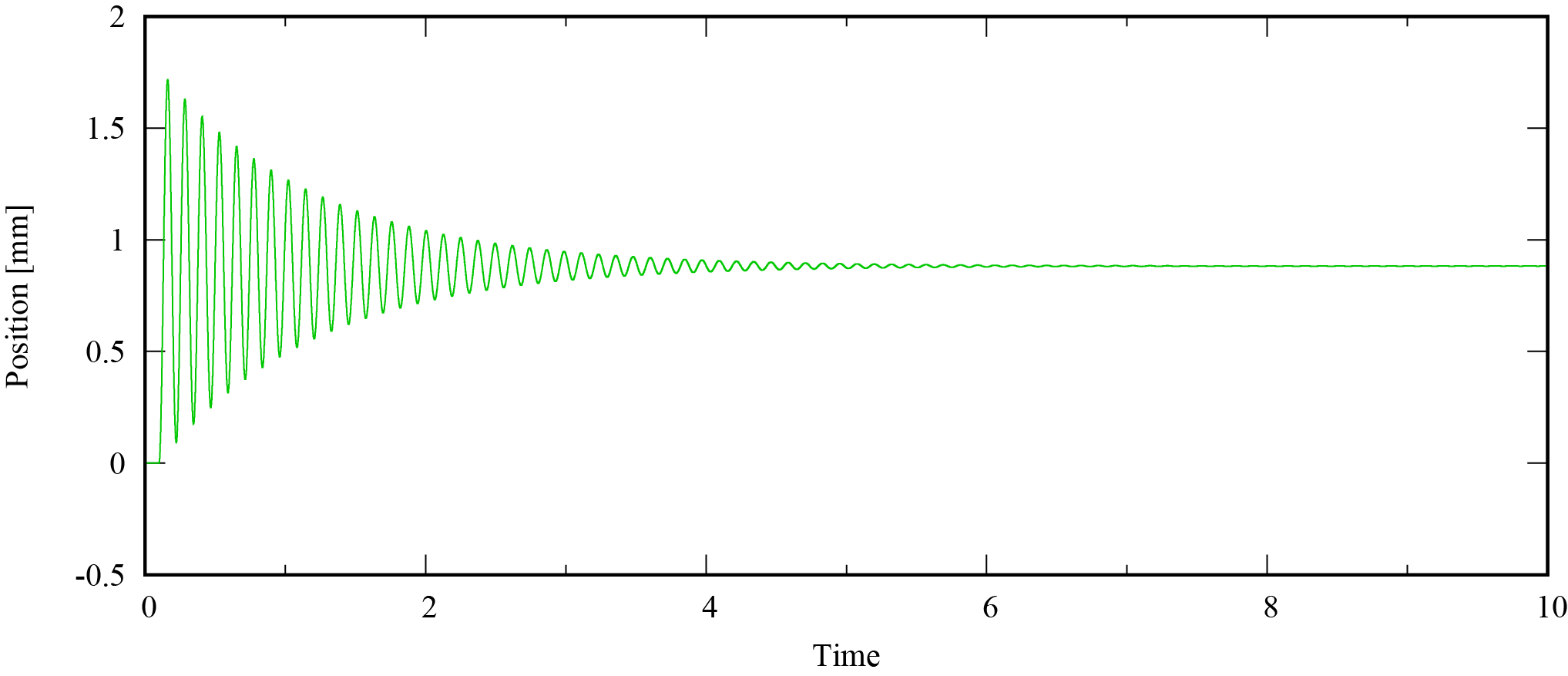
この時系列を用いて,モデルを作成していきます。
2019/10/31 追記
システム同定のやりかた?のような物を書きました。
https://qiita.com/wcrvt/items/e9188249a728582f162d
モデル化
制御工学では,システムを状態空間表現を用いたモデルを使用します。
\dot{x}=Ax+Bu\\
y=Cx
$x$は状態,$y$は観測値,$u$は入力です。$A$,$B$,$C$は状態(遷移)行列,入力行列,観測行列と呼ばれます。$A$は状態$x$の自由運動を表すパラメータ,Bは入力$u$の影響度を表すパラメータとなります。上のシステムの運動方程式を書くと,
f=-(kx+d\dot{x})+F_{\rm motor}=m\ddot{x}\\
\iff \ddot{x}=-\frac{1}{m}(kx+d\dot{x})+\frac{1}{m}F_{\rm motor}
となり,状態空間表現を次のように作ることができます。
\begin{bmatrix}
\dot{x} \\ \ddot{x}
\end{bmatrix}
=
\begin{bmatrix}
0 & 1\\
-\frac{1}{m}k & -\frac{1}{m}d
\end{bmatrix}
\begin{bmatrix}
x \\ \dot{x}
\end{bmatrix}
+
\begin{bmatrix}
0 \\ \frac{1}{m}
\end{bmatrix}
F_{\rm motor}\\
\iff
\frac{d}{dt}
\begin{bmatrix}
x \\ \dot{x}
\end{bmatrix}
=
\begin{bmatrix}
0 & 1\\
-\frac{1}{m}k & -\frac{1}{m}d
\end{bmatrix}
\begin{bmatrix}
x \\ \dot{x}
\end{bmatrix}
+
\begin{bmatrix}
0 \\ \frac{1}{m}
\end{bmatrix}
F_{\rm motor}
入力不確かさ$v$や観測誤差$w$があると次のように表現されます。
\dot{x}=Ax+Bu+v\\
y=Cx+w
そして,運動の流れを示すブロック線図は次のようになります。
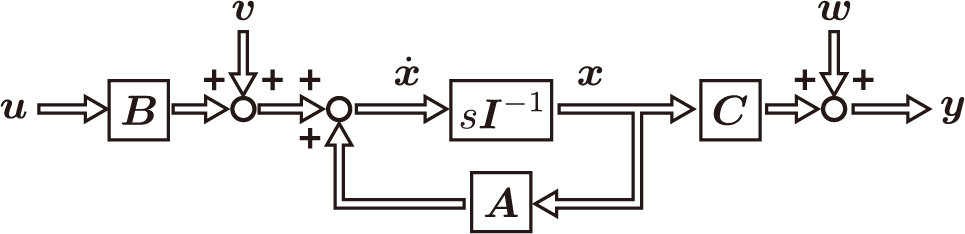
これは連続時間モデルと呼ばれますが,予測を行うときには都合がよくありません。そのため,離散時間モデルに変換します。
x[k+1]=A_dx[k]+B_du[k]\\
y[k]=C_dx[k]\\
\left(A_d=e^{AT_s},
B_d=\int^{T_s}_0 e^{A\tau}d\tau B,
C_d=C\right)
$T_s$はサンプリング時間です。上記の例は,入力$u$が区間内一定値をとる場合の厳密離散化です。どうやって変換しているかというと,まず連続時間状態空間表現の微分方程式を解いて時間応答を求めます。
x(t)=e^{At}x_0+\int^t_0 e^{A(t-\tau)}Bu(\tau) d\tau
ここで,$x_0$は状態量の初期値を表す。右辺第一項は初期値に対する自由運動を表し,第二項の畳み込み積分はインパルス応答の蓄積値を表す。任意サンプル時刻$kT_{\rm s}$と次回サンプリング時刻$(k+1)T_{\rm s}$の状態の関係は以下のようになる。
x((k+1)T_{\rm s})=e^{A(k+1)T_{\rm s}}x_0+\int^{(k+1)T_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau\\
=e^{AT_{\rm s}}e^{AkT_{\rm s}}x_0+e^{AT_{\rm s}}\int^{(k+1)T_{\rm s}}_{kT_{\rm s}} e^{A(kT_{\rm s}-\tau)}Bu(\tau) d\tau + \int^{kT_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau\\
=e^{AT_{\rm s}}x(kT_{\rm s})+\int^{kT_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau
ここで,入力$u$が区間内一定であるとすると,次式のように変形できる。
x((k+1)T_{\rm s})=e^{A}T_{\rm s}x(kT_{\rm s})+\int^{(k+1)T_{\rm s}}_{kT_{\rm s}} e^{A((k+1)T_{\rm s}-\tau)} d\tau Bu(kT_{\rm s})
また,積分計算において変数$\gamma=-\tau+(k+1)T_{\rm s}$を導入することで,次式を得る。
x((k+1)T_{\rm s})=e^{AT_{\rm s}}x(kT_{\rm s})+\int^0_{T_{\rm s}}e^{A\gamma} (-d\gamma) Bu(kT_{\rm s})\\
=e^{AT_{\rm s}}x(kT_{\rm s})+\int^{T_{\rm s}}_{0} e^{A\gamma} d\gamma Bu(kT_{\rm s})
時刻$kT_{\rm s}$における状態および入力を$x[k],\ u[k]$と書くと,離散時間状態空間表現のパラメータは次のようになる。
A_d=e^{AT_s},
B_d=\int^{T_s}_0 e^{A\tau}d\tau B,
C_d=C
証明終了。
なので,連続時間のモデルを作ってから離散時間モデルを作成することができます。しかしながら,離散時間空間でモデル化を行なった方が,モデル化の精度が高くなります。理由は,離散時間モデルの表現方法と評価回数の多さにあります。これを確認するために,離散時間空間でのモデルの表現と同定方法を確認していきます。
ARXモデルの同定
常微分方程式に支配される運動は,過去の運動に影響されて現在の運動が決定します。たとえば,位置は速度の積分値であり,前時刻の位置と速度から現在の位置が決まります。したがって,離散時間空間では時系列は次のように表現できます。
x[k]=A_1x[k-1]+A_2x[k-2]+...A_n[k-n]+B_1u[k-1]+...B_m[k-m]
過去の状態量をいくつ使用するかは設計者の経験に依存するところですが,$A$に関しては微分方程式の階数分の状態量(制御工学では極の数に相当します),$B$は入力の零点の個数を見て決めれば良いと思います。なぜこのモデルが良いかというと,パイプラインのように各時刻でモデルの妥当性を検証できるからです。つまり,N点サンプルすれば,(N-過去の状態量の個数)回の評価ができます。システムには雑音が存在しますので,複数の評価を行うことで妥当性を上げていくことができます。
このモデルと実測値を比較して,誤差の和が最小化すれば,それは精度の良いモデルが得られたということになります。評価を数式で表すと,次のようになります。
J=\sum (y[k]-\hat{y}[k])^2=\sum (y[k]-\theta\phi)^2\\
\theta=
\begin{bmatrix}
A_1 & A_2 & ... & A_n & B_1 & ... & B_m
\end{bmatrix}\\
\phi=
\begin{bmatrix}
x[k-1] & x[k-2] & ... & x[k-n] & u[k-1] & ... & u[k-m]
\end{bmatrix}\\
ここで,$\theta$はパラメータセット,$\phi$はデータセットになります。この$J$を最小化する$\theta$が見つかれば,良いパラメータセットに違いありません。$J$は二乗関数なので凸関数なので,$\frac{d}{d\theta}J=0$となる$\theta$を探す問題となります。
J=\frac{1}{N}\sum_{k=1}^N\left( y^2[k]-2\theta^{\mathrm T}\phi[k]y[k]+\theta^{\mathrm T}\phi[k]\phi^{\mathrm T}[k]\theta\right)\\
=\frac{1}{N}\sum_{k=1}^Ny^2[k] -2\theta^{\mathrm T}\frac{1}{N}\sum_{k=1}^N \phi[k]y[k]+\frac{1}{N}\theta^{\mathrm T}\left(\sum_{k=1}^N\phi[k]\phi^{\mathrm T}[k]\right)\theta\\
\therefore \frac{d}{d\theta}J=-\frac{2}{N}\sum_{k=1}^N \phi[k]y[k] + \frac{2}{N}\left(\sum_{k=1}^N\phi[k]\phi^{\mathrm T}[k]\right)\theta
したがって,パラメータベクトル$\theta$の満たすべき条件は次のようになる。
\theta=\left(\sum_{k=1}^N\phi[k]\phi[k]^{\mathrm T}\right)^{-1}\sum_{k=1}^N \phi[k]y[k]
これを解くプログラムは次のようになります。
import numpy as np
import pandas as pd
import json
import math
def fifo(src,a):
p=np.roll(src,1)
p[0]=a
return p
ARX_Psize=2
ARX_Usize=1
x_vec=np.zeros(ARX_Psize)
u_vec=np.zeros(ARX_Usize)
y=0
u=0
yz1=0
uz1=0
phi=np.zeros(ARX_Psize+ARX_Usize)
Phi=np.zeros((ARX_Psize+ARX_Usize,ARX_Psize+ARX_Usize))
Psi=np.zeros(ARX_Psize+ARX_Usize)
# ARX
f = open("result.txt","r")
for i in f.readlines():
data = i[:-1].split(' ')
t = float(data[0])
uz1=u
yz1=y
u=float(data[1])
y=float(data[2])
u_vec = fifo(u_vec,uz1)
x_vec = fifo(x_vec,yz1)
phi=np.hstack((x_vec,u_vec))
Phi+=np.outer(phi, phi.T)
Psi+=y*phi;
f.close()
theta=np.ravel(np.dot(np.linalg.inv(Phi),np.matrix(Psi).T))
print theta
np.savetxt('ModelParam.txt', theta)
ついでに,得られたパラメータに推力指令値を渡した際の応答をシミュレーションするプログラムも用意しました。
# Validation
est=0
x_vec=np.zeros(ARX_Psize)
u_vec=np.zeros(ARX_Usize)
f = open("result.txt","r")
w = open("estimation.txt","w")
for i in f.readlines():
data = i[:-1].split(' ')
t = float(data[0])
uz1=u
u=float(data[1])
y=float(data[2])
u_vec = fifo(u_vec,uz1)
x_vec = fifo(x_vec,est)
phi=np.hstack((x_vec,u_vec))
est=np.dot(theta,phi)
result = "{:.7f} {:.7f} {:.7f}\n".format(t, y, est)
w.write(result)
f.close()
w.close()
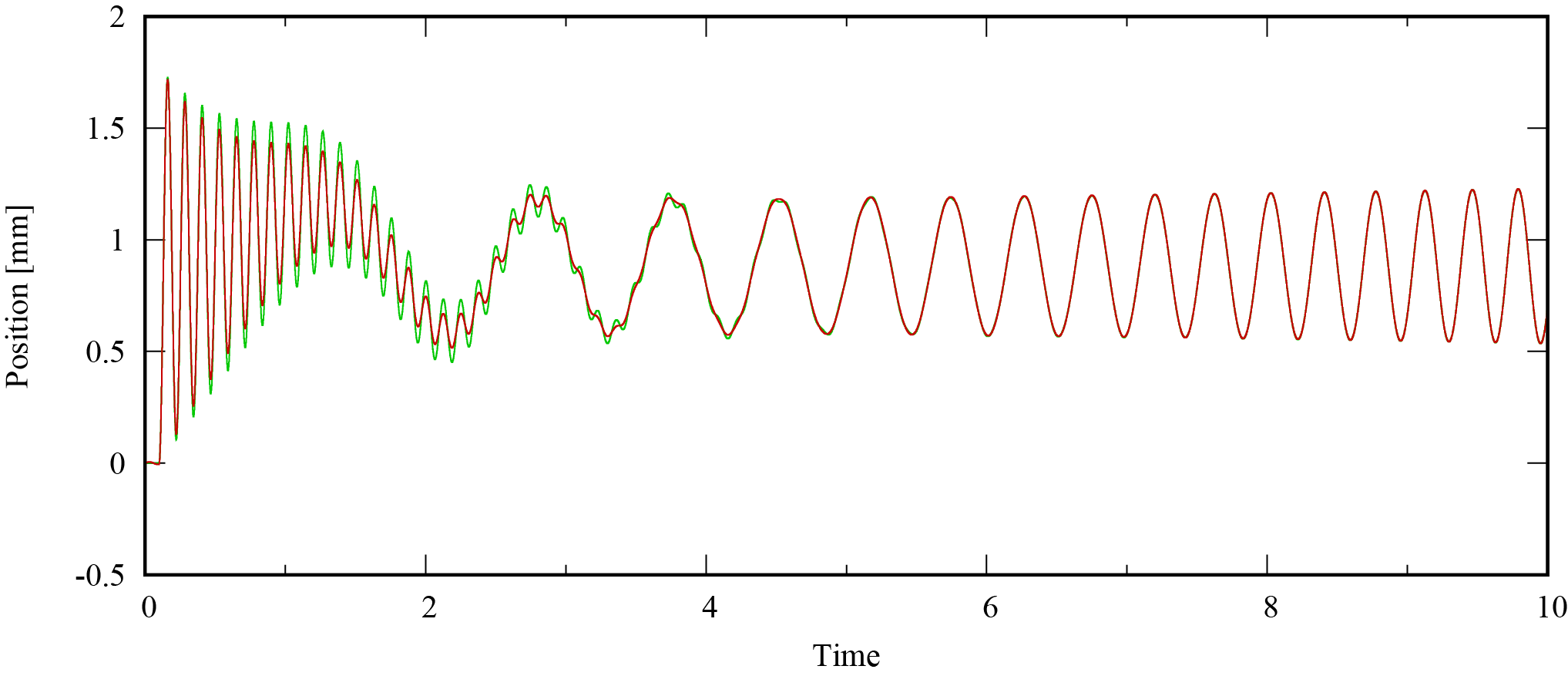
そのときの位置応答値と推定値は次のようになりました。緑は応答値,赤は推定値です。
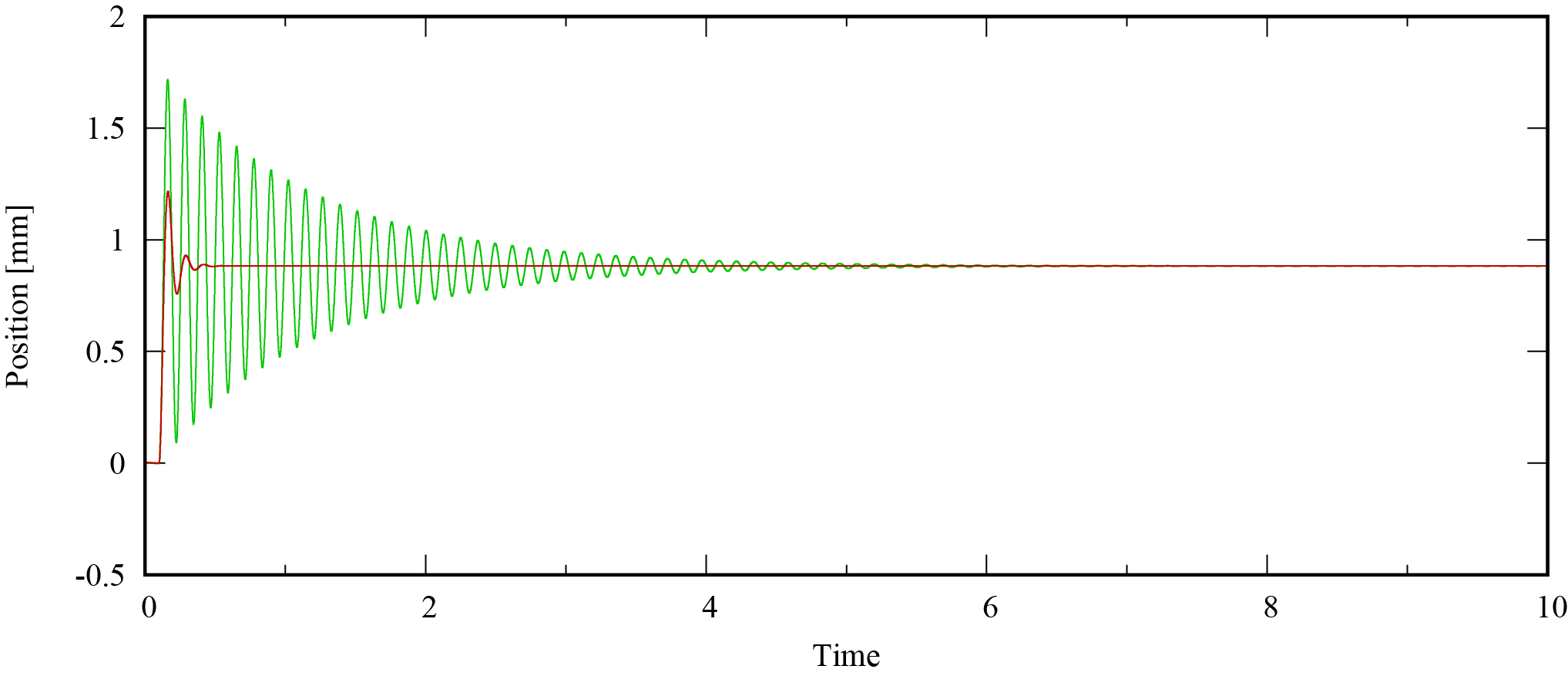
全然推定できていません。これには理由があります。$\theta$を算出するときに,データセットの外積の逆行列を解く必要がありましたが,***入力がシステムの様々な運動を引き起こさないとこの外積内のベクトルに従属関係が生まれ,逆行列の精度が著しく低くなります。***これはPersistent Excitation(PE性)と呼ばれています。そのため,データセットを作る際に入力を工夫します。
force_ref=3.0+math.sin(1.0*time*time) if time>0.1 else 0.0
こうすれば,割としっかり推定されます。ただし,高周波領域の誤差は残りました。これも入力を選定すれば推定可能だとは思いますが,今回はこれくらいで次にいきます。
この試験を雑音を含んだシミュレータを使って行い,パラメータセットが得られればモデル同定完了です。雑音を含んだデータセット作成のプログラムは次のようになります。
import numpy as np
import math
# Time
time=0.0
time_sampling=1e-4
# Motion
position=0
velocity=0
acceleration=0
force=0
# For Integration with Tustin Transformation
velocity_z1=0
acceleration_z1=0
# Environment
env_k=3400
env_d=2.35
env_m=1.3
# Input and Sensor
force_ref=0
position_get=0
# simulator
sim_loop=100
# make data set
f=open("result.txt","w")
while time <= 10:
force_ref=3.0+math.sin(1.0*time*time) if time>0.1 else 0.0
force=force_ref+np.random.normal(0.0, 0.1)
for i in range(sim_loop):
#Position
position+=(velocity+velocity_z1)*time_sampling/sim_loop/2.0
velocity_z1=velocity
#Velocity
velocity+=(acceleration+acceleration_z1)*time_sampling/sim_loop/2.0
acceleration_z1=acceleration
#Acceleration
acceleration=(-env_k*position-velocity*env_d+force)/env_m
position_get=position+np.random.normal(0.0, 0.0001)
result = "{:.7f} {:.7f} {:.7f}\n".format(time, force_ref,position_get)
f.write(result)
time+=time_sampling
f.close()
得られた回帰モデルは,次のように状態空間表現することができます。あくまで一例です。
\begin{bmatrix}
x[k+1]\\x[k]
\end{bmatrix}
=
\begin{bmatrix}
A_1 & A_2 \\ 1 & 0
\end{bmatrix}
\begin{bmatrix}
x[k]\\x[k-1]
\end{bmatrix}
+
\begin{bmatrix}
B_1\\0
\end{bmatrix}
u[k]\\
y[k]=
\begin{bmatrix}
1&0
\end{bmatrix}
\begin{bmatrix}
x[k]\\x[k-1]
\end{bmatrix}
オブザーバの設計
オブザーバの動作原理は,「予測」して「補正」するです。まずはプラントと同じように動作するシステムモデルを作成して,予測してみます。
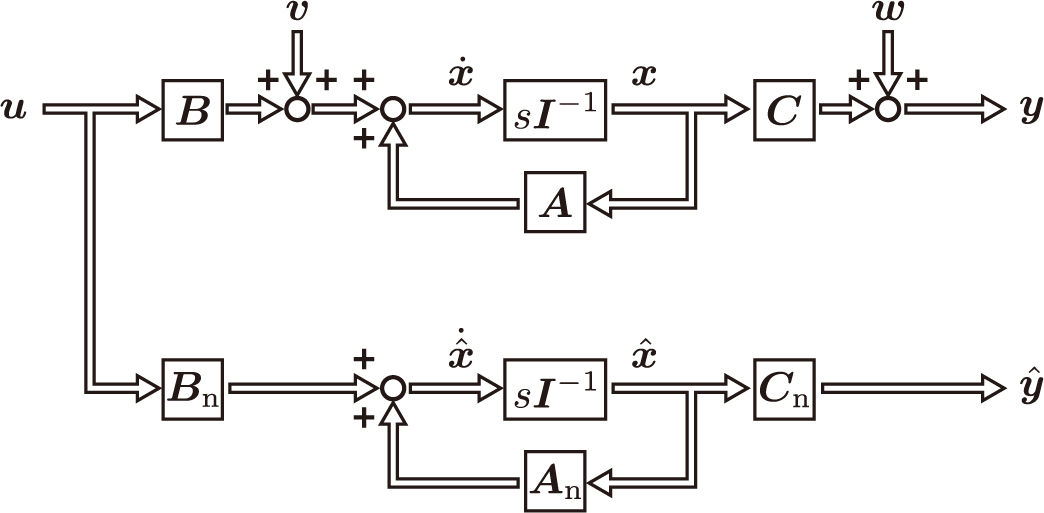
予測はできますが,予測値が真値である保証はどこにもありません。試しに,予測を行うプログラムを作成して実行してみました。
import numpy as np
import math
theta=np.loadtxt('ModelParam.txt')
# Time
time=0.0
time_sampling=1e-4
# Motion
position=0
velocity=0
acceleration=0
force=0
# For Integration with Tustin Transformation
velocity_z1=0
acceleration_z1=0
# Environment
env_k=3400
env_d=2.35
env_m=1.3
# Input and Sensor
force_ref=0
position_get=0
# simulator
sim_loop=100
def fifo(src,a):
p=np.roll(src,1)
p[0]=a
return p
ARX_Psize=2
ARX_Usize=1
x_vec=np.zeros(ARX_Psize)
u_vec=np.zeros(ARX_Usize)
phi=np.zeros(ARX_Psize+ARX_Usize)
y_est=0
# make data set
f=open("response.txt","w")
while time <= 10:
force_ref=3.0+math.sin(1.0*time*time) if time>0.1 else 0.0
force=force_ref+np.random.normal(0.0, 0.1)
for i in range(sim_loop):
#Position
position+=(velocity+velocity_z1)*time_sampling/sim_loop/2.0
velocity_z1=velocity
#Velocity
velocity+=(acceleration+acceleration_z1)*time_sampling/sim_loop/2.0
acceleration_z1=acceleration
#Acceleration
acceleration=(-env_k*position-velocity*env_d+force)/env_m
y_est=np.dot(theta,phi)
position_get=position+np.random.normal(0.0, 0.0001)
u_vec = fifo(u_vec,force_ref)
x_vec = fifo(x_vec,y_est)
phi=np.hstack((x_vec,u_vec))
result = "{:.7f} {:.7f} {:.7f} {:.7f} {:.7f}\n".format(time, force_ref,position,position_get,y_est)
f.write(result)
time+=time_sampling
f.close()
実行結果は次のようになりました。緑は測定位置,青は実位置,赤は予測値です。
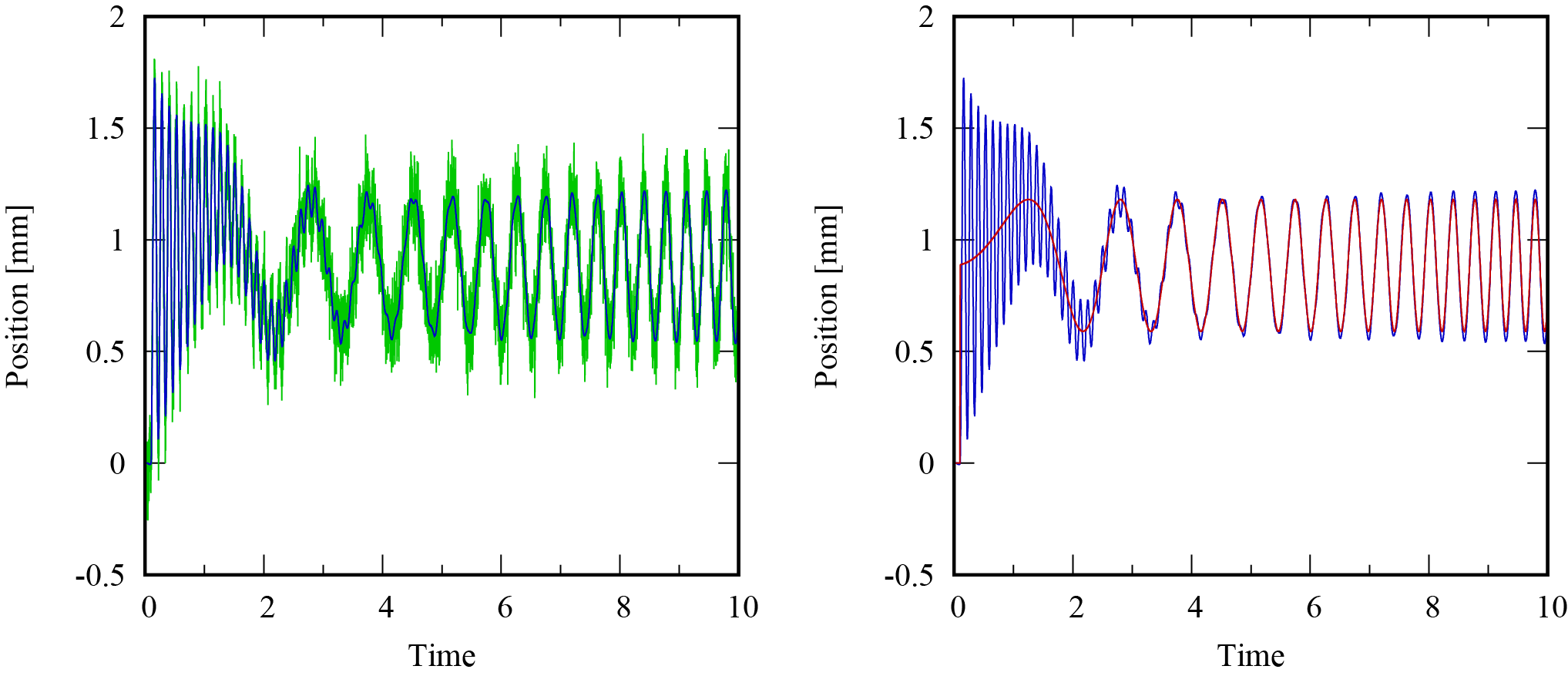
予測値は雑音成分があまり含まれていませんが,入力成分由来の実位置変動を捉えられていません。そこで,フィードバックループを追加して予測値の補正を行います。
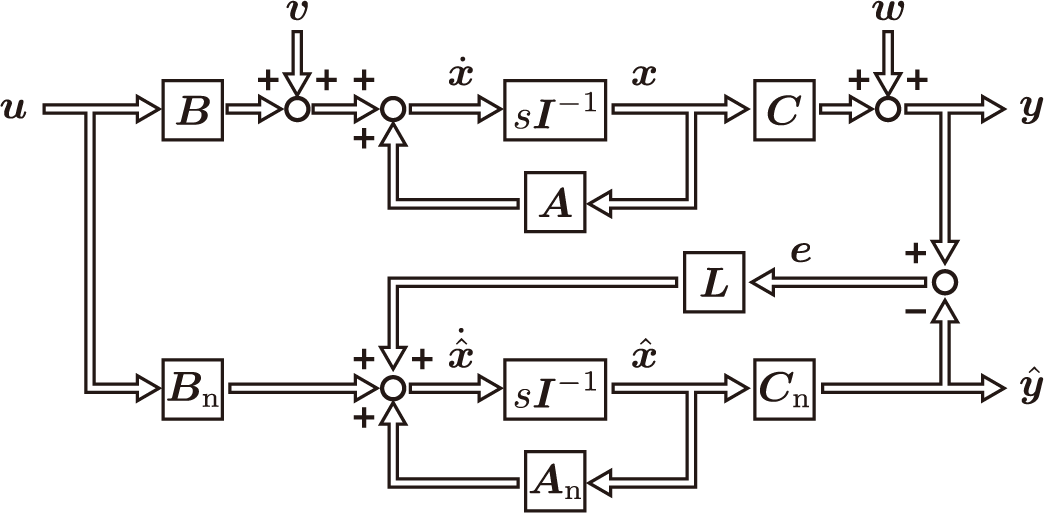
これをLuenbergerのオブザーバと呼びます。このオブザーバがなぜ動作するかについては,ここでは割愛します。このオブザーバの動作を確認するために,プログラムを1行だけ編集します。
y_est=np.dot(theta,phi)+0.4*(position-y_est)
ここでは,オブザーバゲイン$L=0.4$としています。この時の推定結果は以下のようになりました。
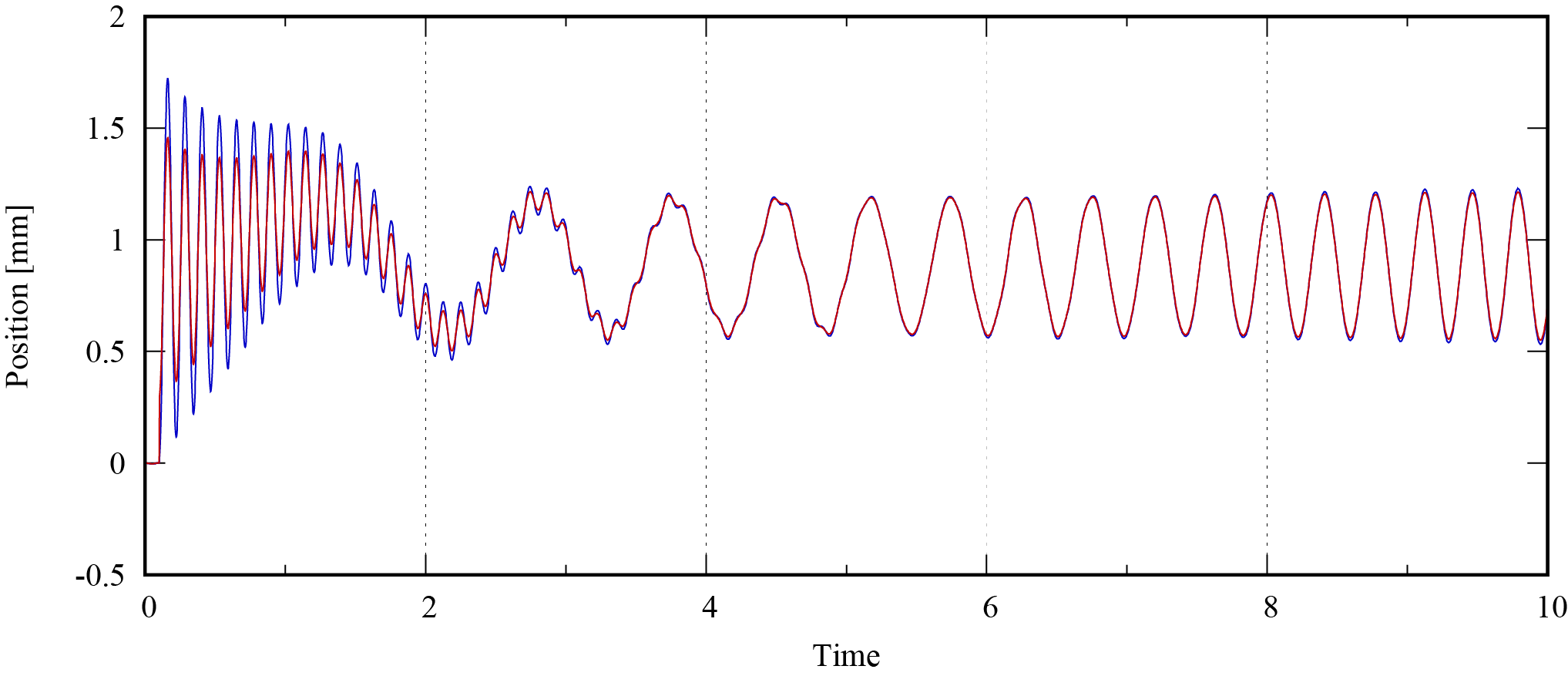
これにより,単純な予測では得られなかった推定が可能になりました。
おわりに
カルマンフィルタは,Luenbergerオブザーバのクラスに属します。カルマンフィルタの何が凄いかというと,オブザーバゲインが推定誤差の分散を最小化する(最小二乗推定)ように決定されるという点です。このカルマンゲインの決定は,気が向いたら書ければと思います。
(6月12日追加) この記事を事前知識として知っていると、足立先生の解説論文が見やすいかもしれません。
足立修一、線形カルマンフィルタの基礎、計測と制御、56巻、9号、pp. 632-637、2017
https://www.jstage.jst.go.jp/article/sicejl/56/9/56_632/_article/-char/ja/
一応,Luenbergerオブザーバから最小二乗推定を行おうとすると,カルマンフィルタと同様の形式のフィルタが導出されます。導出をここに置いておきます。Luenbergerオブザーバの一般化推定式は次のようになります。
\hat{x}[k+1]=F\hat{x}[k]+B_du[k]+Ly[k]
(k+1)ステップでの推定誤差は,次のようになります。
e[k+1]=(A_d-LC_d-F)x[k]\\
+A_de[k]+v-Lw.
ここで,プロセス雑音および観測雑音の平均値が0であるとすれば,推定誤差の期待値は次のようになります。
{\rm E}\{e[k+1]\}=(A_d-LC_d-F){\rm E}\{x[k]\}+F{\rm E}\{e[k]\}.
推定誤差の差分方程式が上式のように表される中で,関数を最小化する条件は$F=A_d-LC_d$となります。また,推定誤差の分散に関しては次のようになります。
P[k+1]=FP[k]F^{\mathrm T}+Q+LRL^{\mathrm T}\\
P[k]:={\rm E}\{e[k]e^{\mathrm T}[k]\}.
ここで,$P[k]$は共分散行列と呼ばれます。$Q$,$R$はプロセス雑音の分散,Rは観測雑音の分散です。最適な$L$を得るためには変分法が有効です。$P[k]$を$L$の関数($P[k]=f(L)$)と見ると,$L$は次の式を満たす必要があります。
\forall \varepsilon,\ f(L+\varepsilon)-f(L)\geq0.
したがって,次の式を得ます。
L=A_dP[k]C_d(R+C_dP[k]C_d^{\mathrm T})^{-1}.
したがって,最小二乗推定のプロセスは以下のように実現されることがわかりました。
\hat{x}[k+1]=A_d\left\{(I_n-KC_d)\hat{x}[k]+Ky[k]\right\}+B_du[k]\\
K=P[k]C_d(R+C_dP[k]C_d^{\mathrm T})^{-1}\\
P[k+1]=A_d(I_n-KC_d)P[k]A^{\mathrm T}_d+Q
この式をよく見て見ると,カルマンフィルタと一緒です。この導出からわかるように,線形時不変系では雑音の色,分布,相関に関わらずカルマンフィルタを組めば最小二乗推定が達成されるとも見ることができます。
また,カルマンフィルタを使用しなくても,FPGAを使えば雑音成分が削れたりするので,宜しければご覧ください。
https://qiita.com/tvrcw/items/3dbb27a1798b737ffb3f
拙文ですが,制御工学の基礎を纏めた資料を公開しております。宜しければこちらもご覧ください。
https://craftservo.com/textbook/BasicControl1.pdf