システム同定を学習するためのToolBox

#はじめに
軽量なシステム同定用ToolBoxが欲しくなったので作ろうと思ったのですが，実運用するためには様々な機能(後述)を搭載する必要があり，作るのを止めていたのですが，システム同定の勉強用には良い教材になりそうなので公開しようと思います。

前記事 https://qiita.com/wcrvt/items/cd1930598ef72055d20b に記載しているように，カルマンフィルタを設計する上でもシステム同定は非常に重要な準備です。システム同定の原理等は上記記事にあります。

Qtでアプリケーションを作成しています。実行ファイルとソースコードは以下にあります。
https://github.com/wcrvt/SystemIdentification
Macで開発したため，Macのみ実行可能です。Winでソースをコンパイルすれば実行可能になります(要FFTW)。システム同定，FFTのコードがソース内にありますので，そちらだけ欲しい人は持って行ってください。

*このアプリケーションは実際に測定したデータセットを使うと良いモデルが出なかったりします。あくまでも勉強用です。

##動作

アプリケーションを開くと，次のような画面が立ち上がります。

ここに，時系列のデータを渡します。データフォーマットは.datもしくは.csvを読み込めます。データが正常に読み込めない場合はデータの区切りを変更してLoadすると直ります。今回は勉強用として，理想的な条件でデータを入力・観測できた場合のデータセットを作成し，アプリケーションに渡します(ソースコード内にデータセット生成用のプログラムがあります)。

dataset.py

import numpy as np
import math

#Time
time=0.0
time_sampling=1e-4

#Motion
position=0
velocity=0
acceleration=0
force=0

#For Intefgration with Tastin Transformation
velocity_z1=0
acceleration_z1=0

#Environment
env_k=3400
env_d=2.35
env_m=1.3

#Input and Sensor
force_ref=0
position_get=0

#simulator
sim_loop=100

#make data set
f=open("b.dat","w")
while time <= 50:
    force_ref=10.0*math.sin(5.0*time*time) if time>0.1 else 0.0
    force=force_ref+np.random.normal(0.0, 0.001)
    for i in range(sim_loop):
        #Position
        position+=(velocity+velocity_z1)*time_sampling/sim_loop/2.0 
        velocity_z1=velocity
        #Velocity
        velocity+=(acceleration+acceleration_z1)*time_sampling/sim_loop/2.0
        acceleration_z1=acceleration
        #Acceleration
        acceleration=(-env_k*position-velocity*env_d+force)/env_m
    position_get=position+np.random.normal(0.0, 50e-9)
    result = "{:.7f} {:.7f} {:.7f}\n".format(time, force_ref,position_get)
    f.write(result)
    time+=time_sampling
f.close() 

モータで物体を押しているような状況を想定しています。連続時間における推力入力から位置応答までの伝達関数$G(s)$が

G(s)=\frac{1}{1.3s^2+2.35s+3400}

となるようなプラントシミュレータでデータを生成しました。入力にはスイープ信号を使用しています。このデータを読み込むと，時間波形と周波数成分が自動で描画されます。

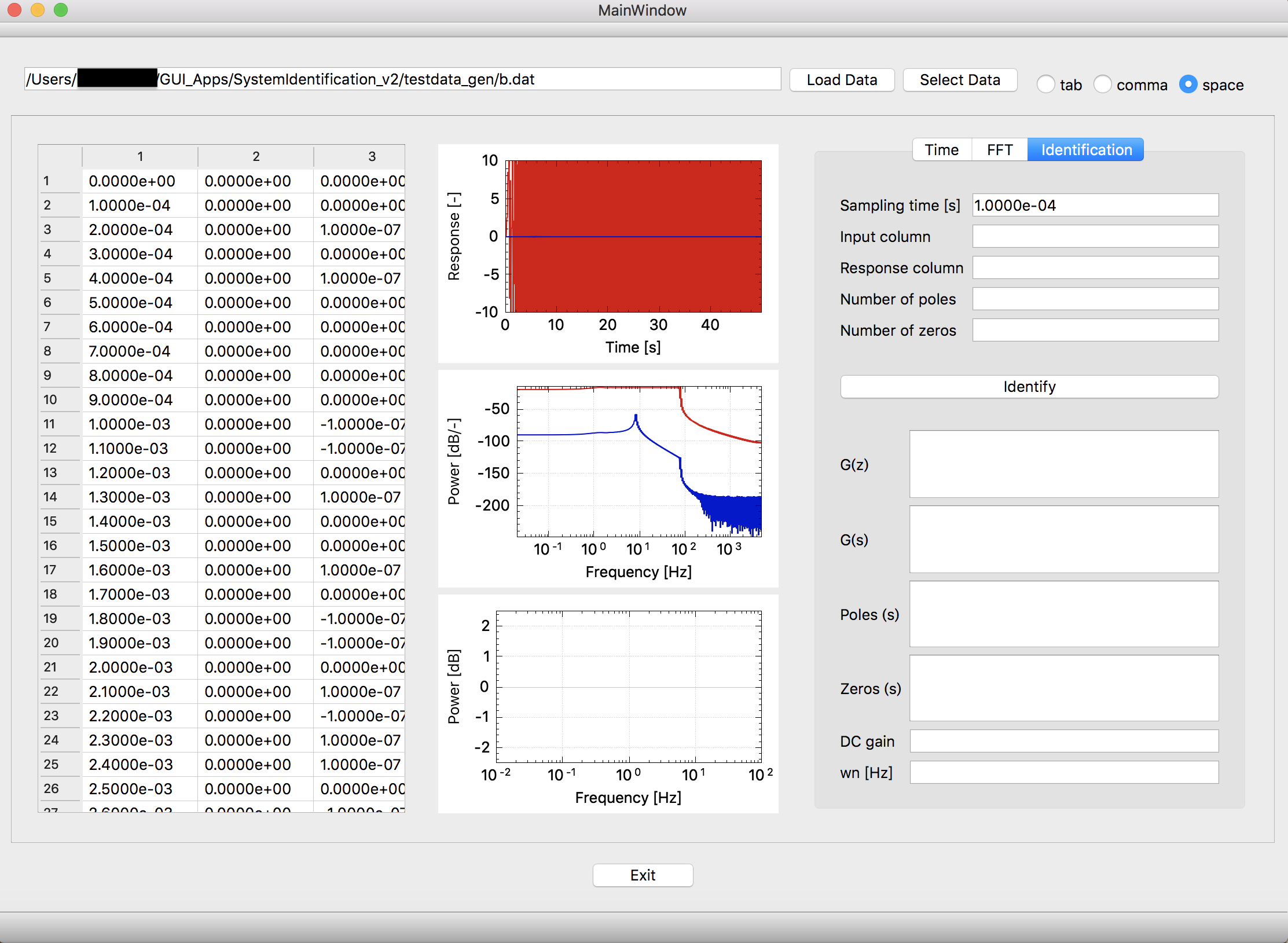
次に，Identificationのタブでデータ内における入力と出力の行数，作成するモデルの次数(極と零点の数)を記入してIdentifyボタンを押すと，離散時間伝達関数，連続時間伝達関数，極，零点，定常ゲイン，固有周波数を算出してくれます。

作成したプラントシミュレータと同様の結果が得られました。そして，一番下のグラフに，入力と出力の周波数成分から得られるだろうゲイン線図とシステム同定で得られたゲイン線図を表示しています。ここの波形が合っていればシステム同定が成功しているといった感じになります。

##使用上の注意

このアプリケーションに実装されているシステム同定は記事 https://qiita.com/wcrvt/items/cd1930598ef72055d20b に記載されている最小二乗法を使用しています。上記時にPE(Persistent Excitation)性とテプリッツ行列の正定値性について軽く触れていますが，システム同定では入力の選定が非常に重要です。簡潔に話すと，連立方程式を解くようなもので，複数の周波数帯における入出力関係がなければ連立方程式を解くための情報が足りていない，といった感じになります。入力にはスイープ信号やM系列信号を使用しますが，各々特徴があるため，確認してみてください。私は位相情報を見るためにスイープ信号の方をよく使います。

この他にも，実運用には多くの問題があります。

• 最小二乗法を行なうためにはテプリッツ行列が正定であると同時にテプリッツ行列の逆行列を正確に導出する必要があります。観測値が大きなDC値を持っていたり，サンプリング周波数が高すぎてサンプル値が非常に近い値を持ったりすると，テプリッツ行列の要素同士が近い値を持つため，計算機の丸め込みの影響を受けて正確な逆行列が算出されないことがあります。慶應義塾大学 足立先生の経験則では,着目する周波数帯域の10倍のサンプリング周波数を使用するのが望ましいとのことです(先生著「システム同定の基礎」より)。上記アプリケーションはデシメーション機能を搭載していません。

• 実際にデータを取得してシステム同定を行なう場合には，観測におけるノイズや位相遅れの影響を考慮する必要があります。観測値がノイズに埋もれてしまう(高周波領域で起こりやすい，これはシステムの駆動帯域の制限により高周波領域の応答が励起されないため)場合には，システム同定がうまく行かない場合が多いです。このような場合には，なるべく振幅の大きな入力を入れるとうまくいくことがあります。また，システム同定は入出力の因果関係に基づくため，位相遅れは大きな誤差要因となります。特に，サンプリング周波数が高い場合には入出力間の時間遅れも目立ち，離散時間表現に時間シフト作用素を入れる必要があります。上記のアプリケーションは時間シフト機能を搭載していません。

• 極と零点の数の決定には，実機の時間応答や周波数応答を確認して，ある程度の枠組みはありますが，経験的に決定する必要があります。「モデル化」とは何かにするにあたり必要な分(本質)だけを記述することですが，制御系設計に必要な分の帯域を見極め，次数を決定したりします。高次モデルを作成して制御系実装ができなくては意味がありませんし，低次モデルを使用して制御系の不安定化を引き起こしてもいけません。低次遅れ系に高次極モデルをフィッティングさせると，支配極がシステムの特性のほとんどを記述して，残りの極は支配極の記述を邪魔しないようにしていたりします。少ない方から選んで行って，フィッティングがうまくできたところで止めたりすると良いかもしれません。

このように，システム同定のアルゴリズム，システムのデバイス特性，入力信号の選定方法等を知らなければシステム同定を行なう以前の問題となります。これはMatlab等を使用しても同じことだと思います。このようにToolBoxを作っても使う人を選ぶことになる予想されますし，実運用上の機能の搭載が非常に面倒なので作成を止めています。興味のある方はご自由にソースコードを使ってください。