はじめに
制御工学専門です。制御系を設計する際,ノイズレベルを如何に減らすかに日々苦心しています。カルマンフィルタに代表される統計フィルタも使用します。ただ,FPGAを使うともっと簡単にノイズレベルの低減が実現できます。
「FPGAを使用するとノイズレベルが減ります」と行った時,「どれくらい?」という話になります。そんな時に定量的なデータを示せる指標を作りましたので参考になれば幸いです。
必要な知識
離散フーリエ変換
フーリエ変換は時間-周波数空間写像です。時間信号を単一周波数の波の集合として捉え,時間信号を構成する周波数成分を出力します。理想的なフーリエ変換は無限の周波数まで使って信号を表現しますが,離散フーリエ変換はナイキスト周波数(サンプリング周波数の半分,離散演算器が認識できる信号の周波数帯域)までの周波数を使って信号を表現します。
パーセバルの定理
フーリエ変換がユニタリであることを示します。細かいことを省くと,時間空間と周波数空間の写像において,エネルギが保存されるということです。離散変換でも成立します。周波数空間上でパワースペクトルを見れば時間信号の特定の周波数成分のパワーが観れます。ノイズのパワーも保存されます。
時空間分解能とノイズパワーの関係
証明は割愛しますが,ノイズパワーと時間・空間分解能には関係式が存在します。下記の式は静的量子化器を使用した際の関係式です。ここで,Ncはノイズパワー,qは量子化器の幅,Kはオーバーサンプリング比です。
N_c = 20\log_{10} q − 10\log_{10} K − 7.78\ {\rm [dB]}
デルタシグマ変調器等の動的量子化器はKを上げてSNRを上げます。動的量子化器ではKの係数が変わります。この式が示すのは,インタフェースの空間分解能を上げる(qを半分にする)と6.02 dB,時間分解能を上げる(サンプリング周波数を2倍)にすると3.01 dBノイズレベルが低減します。ただし,空間分解能に関しては,インタフェース前段に重畳するノイズが量子化幅と比較して大きい場合はこの低減は望めません。今回は,静的量子化器を用いて時間分解能を上げた際にノイズレベルがどれだけ変化するかを示します。
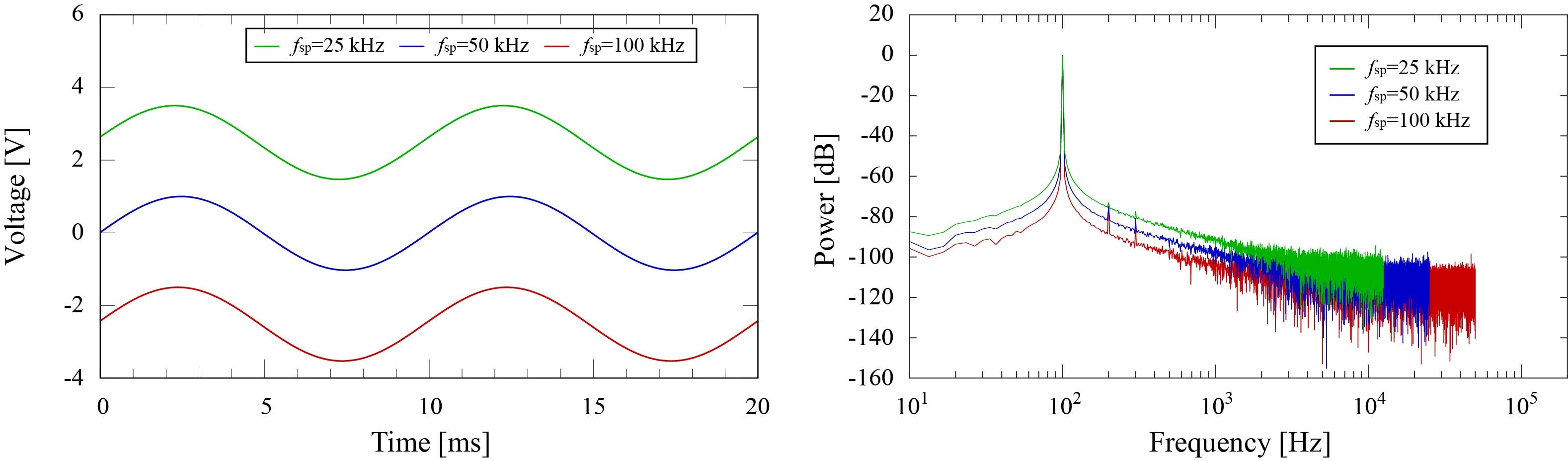
("Experimental Validation of Noise Power in System Under Hardware Constraints", IEEE-ICIT 2019, Feb. 2019から引用)
この図はファンクションジェネータで振幅1,周波数100 Hzの波を発生させ,25 kHz,50 kHz,100kHzで動作するAD変換器で取得したものの時間信号と周波数成分です。時間信号に違いは見られませんが,周波数空間上では3 dBずつパワーが落ちます。ここで確認すべきことは,ナイキスト周波数の違いです。これを考察すると,以下のことが伺えます。
・パーセバルの定理から帯域内のノイズパワーは保存されてる(積分値が一緒)ので,低サンプリング周波数の際の結果は高周波成分のノイズパワーを補填するために低周波数帯域のノイズレベルが上がっている。
・折り返し(エイリアシング)によって高周波成分のノイズが返ってきて低周波数帯域のノイズレベルが上がっている。
どちらの見方でも良いと思います。これが離散処理系の特性という感じです。特筆すべきことは,一般的なノイズフィルタである低域通過フィルタやカルマンフィルタ各種は低周波数帯域に存在するノイズに作用しませんが,サンプリング周波数を上げる手法は全帯域においてノイズレベルを低減します。これだけでもFPGAを使用することの良さが伝わると思います。
マルチレート系でのノイズレベル
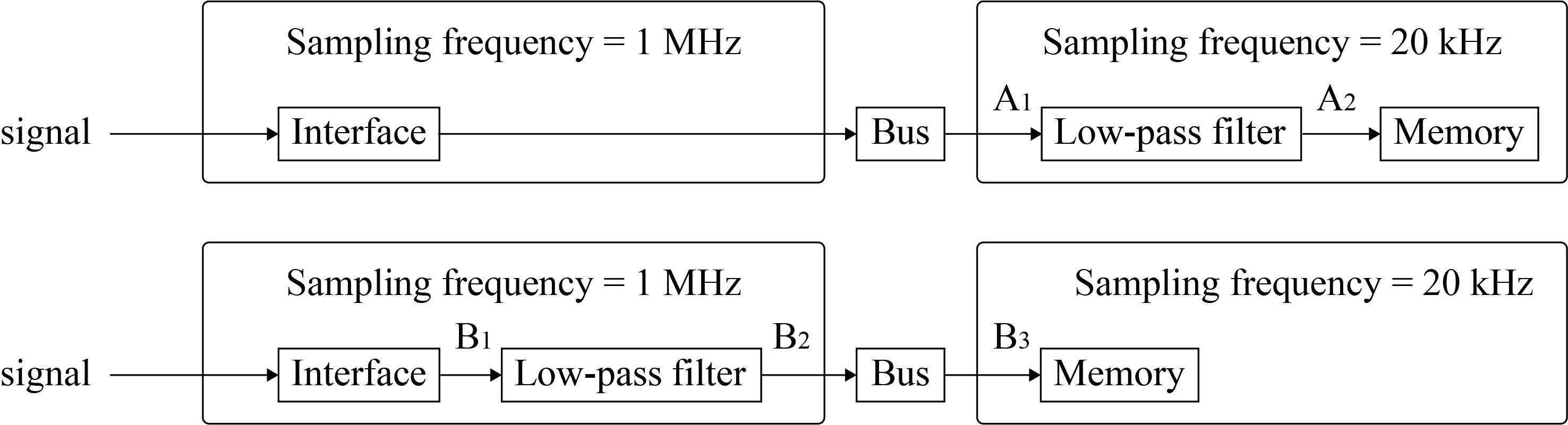
FPGA上で信号処理しても,扱うのはノイマン型のプロセッサが良いと言う方も沢山いらっしゃると思います。そこで,タスクパーティションの一例を示します。
FPGAからプロセッサにデータを送る時には,動作周波数の違いからダウンサンプリングを行います。この時,パーゼバルの定理から二つの時間軸上で信号のパワーは保存されることに留意してください。ここで,低域通過フィルタをFPGAとプロセッサ上に設計するケースを考えます。
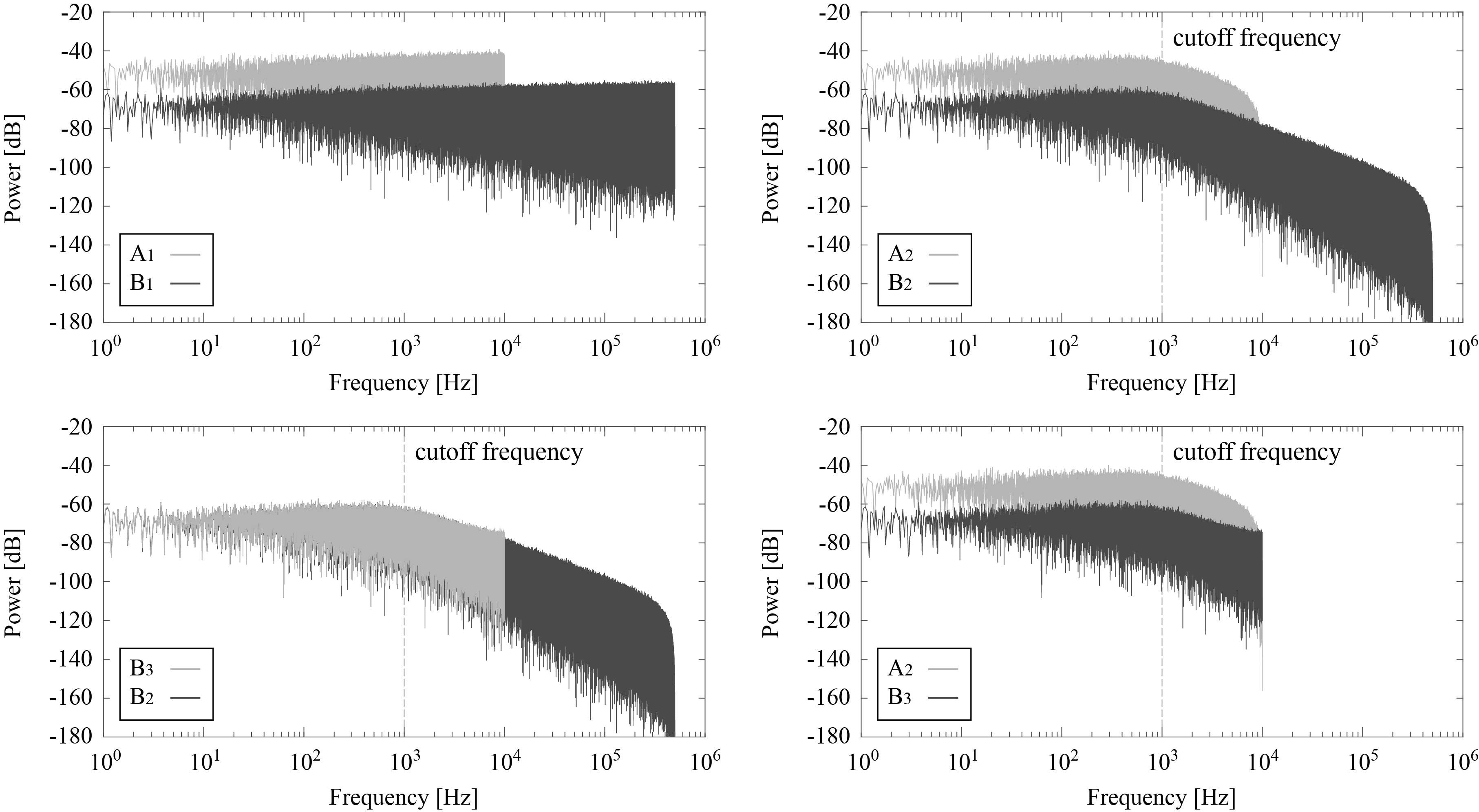
システムへの入力として,ボックスミュラー法で作成した擬似白色雑音を入力します。FPGAおよびプロセッサ上に設計された低域通過フィルタの遮断周波数は1 kHzです。ここで,各点Ai,Biの信号の周波数成分は以下のようになります。
最終的に得られる値はA2およびB3ですが,ノイズレベルに大きな違いが見られます。これはなぜかと言うと,ダウンサンプリングではノイズは保存されますが,低域通過フィルタが除去できるノイズの総量が異なるからです。FPGAでは広帯域のノイズを取り扱えるため,FPGA上に低域通過フィルタを設計した方が多くのノイズを除去できます。FPGAを使用するにあたり,パイプライン化をしてスルーレートを向上するとこのノイズレベル低減効果は増大します。
これらの理由から,複雑なカルマンフィルタをプロセッサ上に設計することは望ましくないと考えています。また,上記フィルタをFPGA上に実装するのも,状況次第だと思います。シンプルに速いことがノイズ処理に一番効果的であると考えているからです。
カルマンフィルタについて
現代制御理論の父と呼ばれるRudolf Kalmanが提案したカルマンフィルタは最小二乗分散推定フィルタであることは有名だと思います。線型近似を使う拡張カルマンフィルタ,Unscentedカルマンフィルタ,最近では高次モーメントを考慮可能であるMaximum correntropy Kalman filterなども現れています。そもそもカルマンフィルタは現代制御で扱われる状態空間表現に基づき,ルーエンバーガのオブザーバの形式で導出されています。そのため,どこまで行っても低域通過フィルタであることには変わらないと思います(Unscentedカルマンフィルタだけあまり知りません)。
簡単なカルマンフィルタの導出から確認してみます。以下の予測ステップ,修正ステップを考えます。
\hat{x}_{\rm p}[k+1]=A_{\rm Tr1}\hat{x}[k]+B_{\rm Tr1}u[k]\\
P_{\rm p}[k+1]=A_{\rm Tr1}P[k]A^{\mathrm T}_{\rm Tr1}+H_{\rm Tr1}QH_{\rm Tr1}^{\mathrm T}\\
\hat{x}[k+1]=(I_n-KC_{\rm Tr1})\hat{x}_{\rm p}[k+1]+Ky[k]\\
P[k+1]=(I_n-KC_{\rm Tr1})P_{\rm p}[k+1]\\
K=P_{\rm p}[k]C_{\rm Tr1}(R+C_{\rm Tr1}P_{\rm p}[k]C_{\rm Tr1}^{\mathrm T})^{-1},
A,B,Cは状態空間表現のシステム行列,入力行列,観測行列,Pは共分散行列,Kはカルマンゲイン,Q,Rはプロセスノイズおよび観測ノイズの分散,添字pは予測値,添字ハットは推定値です。少し式変形すると,次の式を得ます。
\hat{x}[k+1]=(I_n-G)\hat{x}_{\rm p}[k+1]+G(x[k]+C_{\rm Tr1}^{-1}w[k]),\\
G=(H_{\rm Tr1}QH_{\rm Tr1}^{\mathrm T}+A_{\rm Tr1}P[k]A^{\mathrm T}_{\rm Tr1})(C_{\rm Tr1}^{\mathrm -T}RC_{\rm Tr1}^{-1}+H_{\rm Tr1}QH_{\rm Tr1}^{\mathrm T}+A_{\rm Tr1}P[k]A^{\mathrm T}_{\rm Tr1})^{-1}.
これは一般的な離散低域通過フィルタです。Gは遮断周波数になります。周波数Gまでセンサの値を信頼し,それ以降の帯域では予測値を使うというものです。この遮断周波数ですが,QとRの分散の大きさから決定されるのですが,何を示しているかと言うと,入力の精度と観測の精度で遮断周波数を決めるということです。
このカルマンフィルタですが,共分散行列の初期値やノイズの分散や定常性に強く依存します(京都大学の方々が詳しく研究されていたと思います)。したがって,適当に使えばそれなりに効果がでる低域通過フィルタです。QとRの設定で良い結果が出たり出なかったりと,現代制御的にはセンスのないフィルタになりかねないので注意が必要です。
余談ですが,パーティクルフィルタも処理数が必要なのでFPGAでいいかなあ...と思っています。