生命ってコードで作れるの？試してわかったALIFEのヤバさ（前編）

SapeetでSWEをやっている渡辺です。
最近は社内メンバーとARC Raidersにハマっています。
自分も自作ARC（機械生命体）を作ってみたいと思い、Artificial Life（人工生命）に興味を持ちました（）。

なぜ今 ALIFEなのか

ALIFE（Artificial Life の略）は、生命システムを人工的に再現することを目指す分野です。
特に、進化の再現（突然変異など）やパターン創発などの研究が有名です。

例）

• Evolution Gym: 仮想生物の進化を再現した研究
  
• L-system: 植物の構造を再現した研究
  （画像元：wikipedia）

ゆくゆくは人間などの複雑怪奇な生命システムも再現することができれば、病気などの問題の解決に役立てられる研究分野です。

AIとALIFE

大まかに、AIは目的に対して最適化して作られる（トップダウン手法）に対し、ALIFEは偶発的進化に委ねる（ボトムアップ手法）というアプローチの違いがあります。

フィジカルAIの現場でも、人間が作ったアルゴリズムを適用するアプローチから、シミュレーション環境で成長させるアプローチ（Sim2Real）が増えています。

ALIFE試してみた

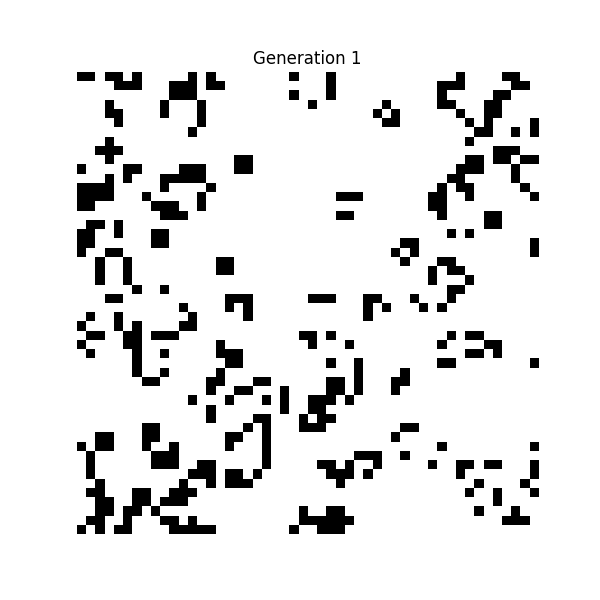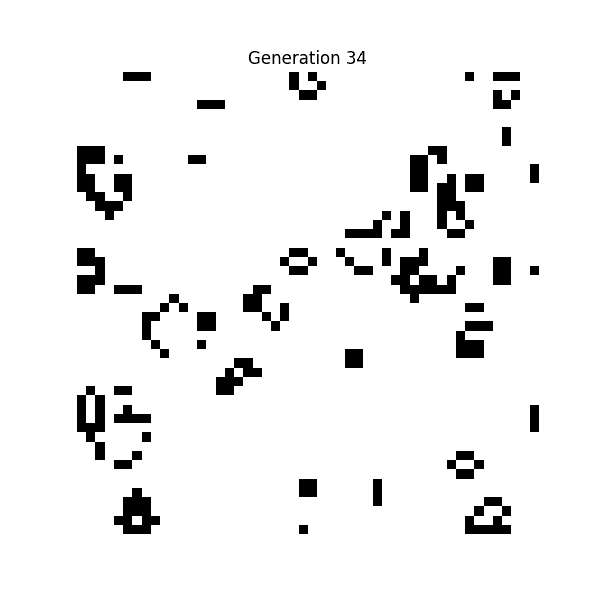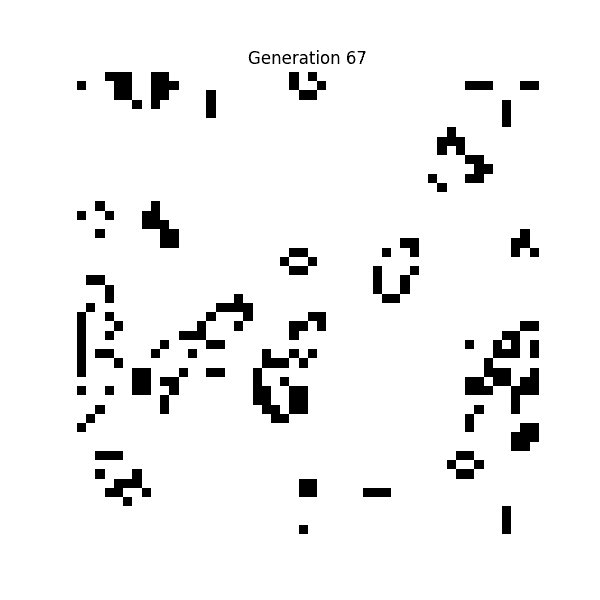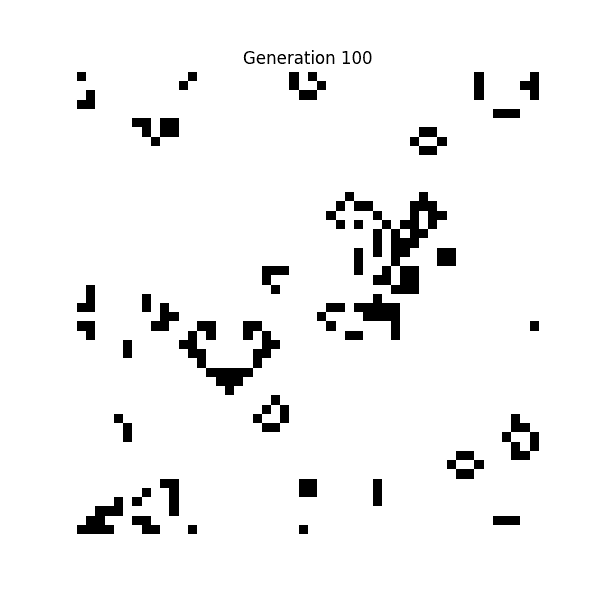
① ライフゲーム（Conway's Game of Life, 1970年）

数学者ジョン・ホートン・コンウェイが考案したセル・オートマトンです。
（※セル・オートマトン ＝ 格子状に並んだ「セル」が、単純な「ルール」に従って自身の状態（色や値など）を時間とともに変化させていく離散的な計算モデル）

白と黒のドットが「過疎なら死ぬ」「適度なら増える」という極めて単純なルールに従って動くだけのシミュレーションですが、これが人工生命研究の原点となったそう。

ライフゲームのルール

• 誕生: 死んでいるセルの周囲にちょうど3つの生きたセルがあれば、次の世代で生まれる
• 生存: 生きているセルの周囲に2つまたは3つの生きたセルがあれば、次の世代でも生き続ける
• 過疎: 生きているセルの周囲に1つ以下の生きたセルしかなければ、孤独で死ぬ
• 過密: 生きているセルの周囲に4つ以上の生きたセルがあれば、過密で死ぬ

ライフゲームを試してみる

💡 単純なルールから、複雑なパターンが創発されているのが確認できます。すぐ消滅してしまうパターンや、長い間存続するパターンも生まれる。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

def game_of_life(size=50, steps=100):
    # ランダムな初期状態を生成
    grid = np.random.choice([0, 1], size=(size, size), p=[0.8, 0.2])

    fig, ax = plt.subplots(figsize=(6, 6))
    img = ax.imshow(grid, cmap='binary')
    ax.set_title('Conway\'s Game of Life')
    ax.axis('off')

    def update(frame):
        nonlocal grid
        # 隣接セルの数をカウント
        neighbors = sum(
            np.roll(np.roll(grid, i, 0), j, 1)
            for i in (-1, 0, 1) for j in (-1, 0, 1)
            if (i != 0 or j != 0)
        )
        # ルールを適用
        grid = ((grid == 1) & (neighbors >= 2) & (neighbors <= 3)) | \
               ((grid == 0) & (neighbors == 3))
        grid = grid.astype(int)
        img.set_array(grid)
        ax.set_title(f'Conway\'s Game of Life - Generation {frame + 1}')
        return [img]

    anim = FuncAnimation(fig, update, frames=steps, interval=100, blit=True)
    plt.close()  # 静止画が出るのを防ぐ
    return HTML(anim.to_jshtml())

# 実行
game_of_life(size=50, steps=100)

---

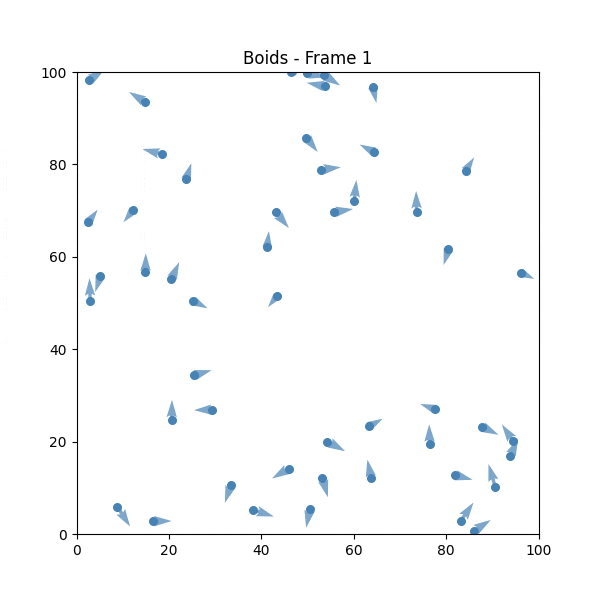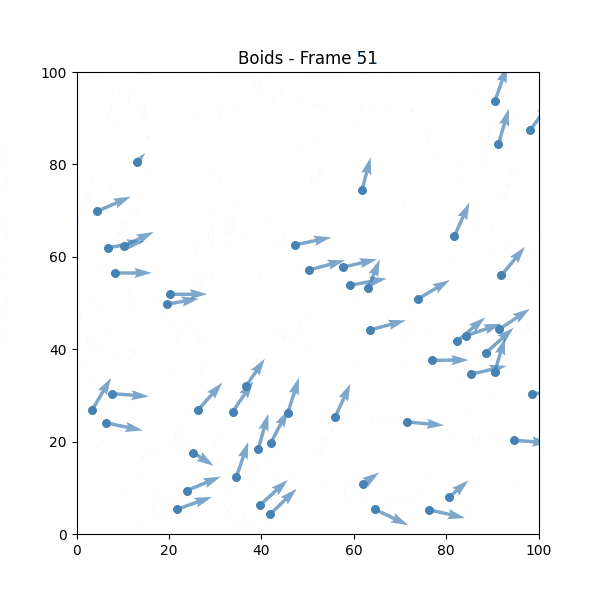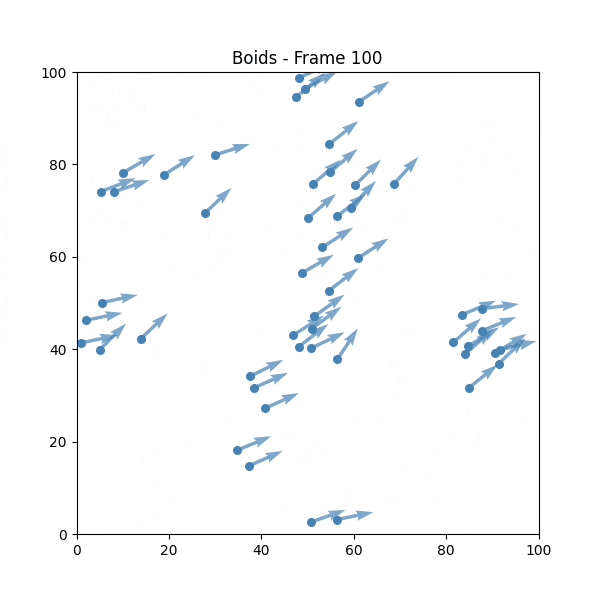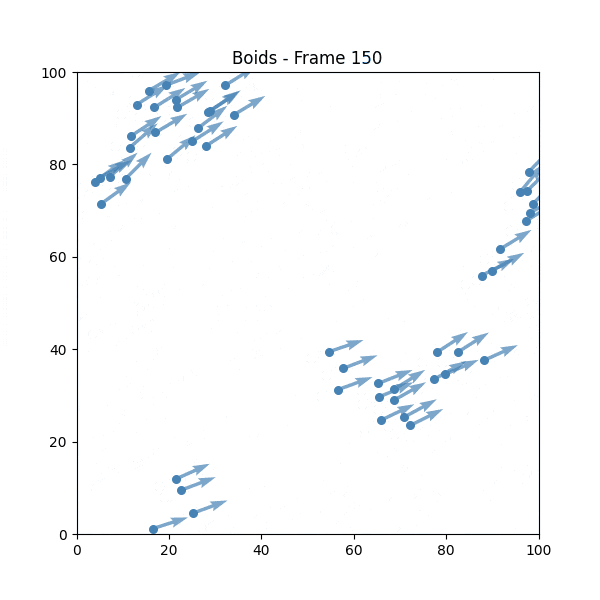
② Boids（1986年）

クレイグ・レイノルズが開発した、群行動をシミュレートするアルゴリズムです。
"Boids"は"bird-oid object"（鳥っぽいオブジェクト）の略です。

Boidsのルール

• 分離: 近くの仲間と衝突しないように距離を取る
• 整列: 近くの仲間と同じ方向に向かおうとする
• 結合: 群れの中心に向かって移動しようとする

Boidsを試してみる

💡 単純なルールでありながら、バラバラな動きから群行動が創発されているのが確認できます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

class Boid:
    def __init__(self, x, y):
        self.position = np.array([x, y], dtype=float)
        angle = np.random.uniform(0, 2 * np.pi)
        self.velocity = np.array([np.cos(angle), np.sin(angle)]) * 2

def boids_simulation(num_boids=50, steps=200):
    width, height = 100, 100

    # 初期化
    boids = [Boid(np.random.uniform(0, width), np.random.uniform(0, height))
             for _ in range(num_boids)]

    fig, ax = plt.subplots(figsize=(6, 6))

    # 初期の位置と速度を取得
    initial_positions = np.array([b.position for b in boids])
    initial_velocities = np.array([b.velocity for b in boids])

    scatter = ax.scatter(initial_positions[:, 0], initial_positions[:, 1], c='steelblue', s=30)
    quiver = ax.quiver(initial_positions[:, 0], initial_positions[:, 1],
                       initial_velocities[:, 0], initial_velocities[:, 1],
                       color='steelblue', scale=50, alpha=0.7)
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)
    ax.set_title('Boids Simulation')
    ax.set_aspect('equal')

    def update(frame):
        for boid in boids:
            neighbors = [b for b in boids if b != boid and
                        np.linalg.norm(b.position - boid.position) < 15]

            if neighbors:
                # 分離: 近すぎる仲間から離れる
                separation = np.zeros(2)
                for n in neighbors:
                    diff = boid.position - n.position
                    dist = np.linalg.norm(diff)
                    if dist < 5:
                        separation += diff / (dist + 0.1)

                # 整列: 近くの仲間の平均速度に合わせる
                alignment = np.mean([n.velocity for n in neighbors], axis=0)

                # 結合: 群れの中心に向かう
                cohesion = np.mean([n.position for n in neighbors], axis=0) - boid.position

                # 力を合成
                boid.velocity += separation * 0.05 + alignment * 0.05 + cohesion * 0.01

            # 速度制限
            speed = np.linalg.norm(boid.velocity)
            if speed > 4:
                boid.velocity = boid.velocity / speed * 4

            # 位置更新（境界でループ）
            boid.position = (boid.position + boid.velocity) % [width, height]

        positions = np.array([b.position for b in boids])
        velocities = np.array([b.velocity for b in boids])

        scatter.set_offsets(positions)
        quiver.set_offsets(positions)
        quiver.set_UVC(velocities[:, 0], velocities[:, 1])
        return scatter, quiver

    anim = FuncAnimation(fig, update, frames=steps, interval=50, blit=True)
    plt.close()
    return HTML(anim.to_jshtml())

# 実行
boids_simulation(num_boids=50, steps=200)

---

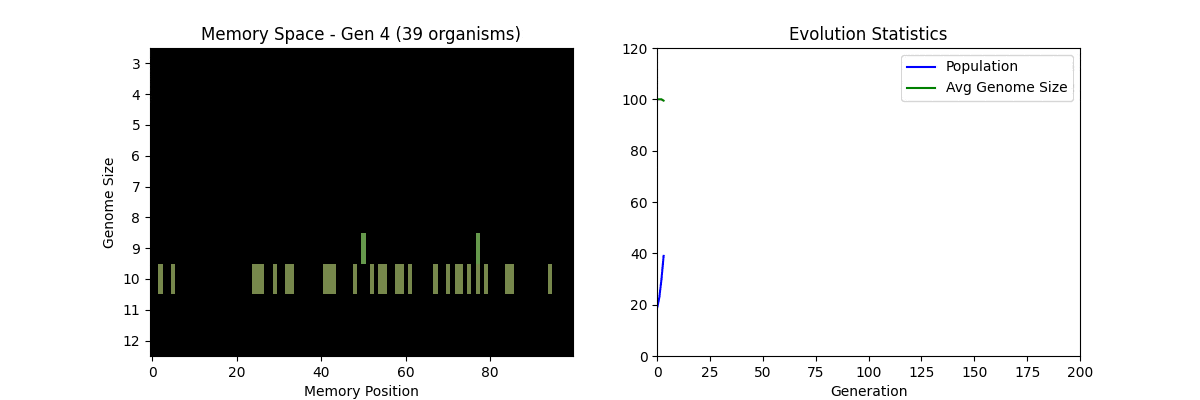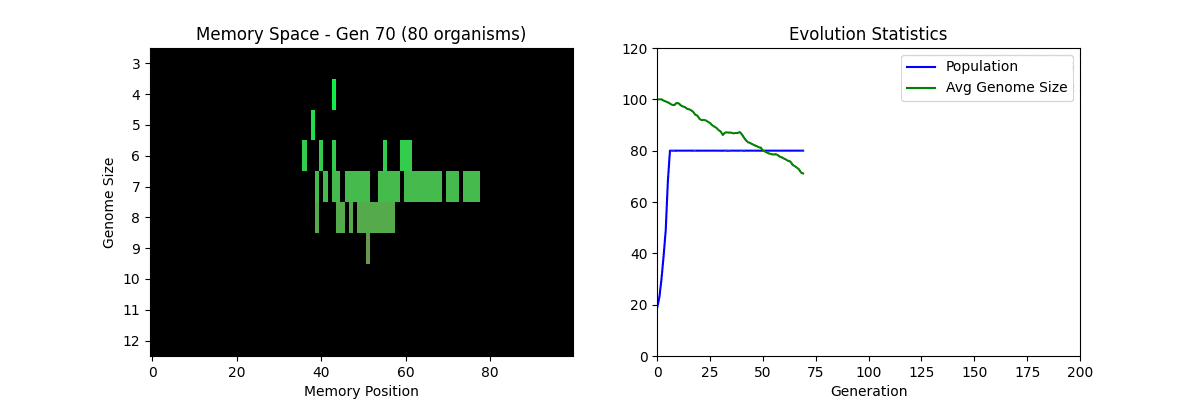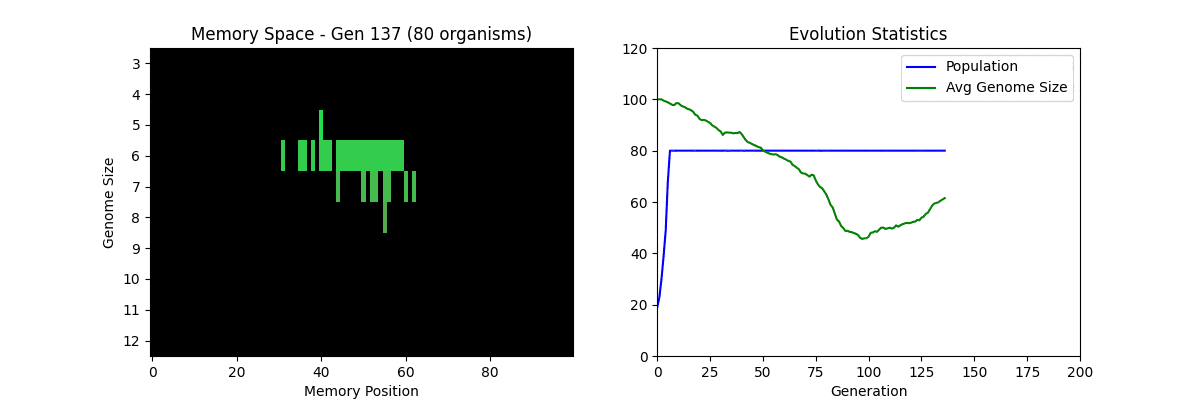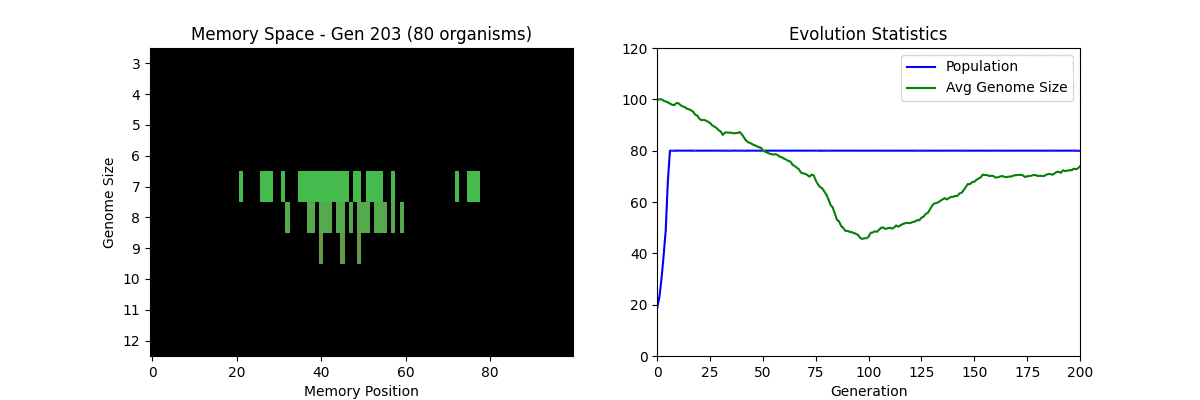
③ Tierra（1990年）

生態学者トーマス・S・レイが開発した、コンピュータ上で遺伝子の突然変異を観察するシステムです。
"Tierra"はスペイン語で「地球」を意味します。

Tierraのルール

Tierraでは、自己複製を行う1個のプログラム（遺伝子コード）を「仮想生物」と見立てます。

• 自己複製: 仮想生物はCPU時間（エネルギー）とメモリー空間（生存領域）を使って自己複製する
• 死: メモリーが80％以上使われると「死神（Reaper）」が現れ、古い個体やエラーの多い個体から消去される
• 突然変異: 宇宙線を模倣し、自己複製時に一定確率で遺伝子コード（CPU命令）のビットが反転する

Tierraを試してみる（簡易版）

本来のTierraは、実際のメモリ上でCPU命令（機械語）が自己複製するシステムです。
ここでは概念を理解しやすくするため、Pythonのリストで「ゲノム」を表現した簡易版を実装しています。

💡 左のメモリ空間で生物の分布が見えます。上=効率的（短いゲノム）、下=非効率（長いゲノム）。進化とともに効率的な短いゲノムの仮想生物が増えている（淘汰されている）ことが確認できます。

Pythonコード

import random
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
from collections import Counter
from IPython.display import HTML

class Organism:
    """デジタル生物: ゲノム（命令列）を持ち、自己複製する"""
    def __init__(self, genome=None, position=None):
        if genome is None:
            self.genome = [random.randint(0, 9) for _ in range(10)]
        else:
            self.genome = genome.copy()
        self.age = 0
        self.errors = 0
        self.position = position if position else random.randint(0, 99)

    def replicate(self, mutation_rate=0.02):
        """自己複製（突然変異あり）"""
        new_genome = []
        for gene in self.genome:
            if random.random() < mutation_rate:
                mutation_type = random.choice(['change', 'insert', 'delete'])
                if mutation_type == 'change':
                    new_genome.append(random.randint(0, 9))
                elif mutation_type == 'insert':
                    new_genome.append(gene)
                    new_genome.append(random.randint(0, 9))
            else:
                new_genome.append(gene)
        if len(new_genome) < 3:
            return None
        return Organism(new_genome, position=(self.position + random.randint(-5, 5)) % 100)

    def fitness(self):
        bonus = self.genome.count(7) * 2
        return 100 - len(self.genome) + bonus - self.errors

    def get_color(self):
        """ゲノムサイズに基づく色（短い=上、長い=下）"""
        size = len(self.genome)
        ratio = min(1.0, max(0.0, (size - 3) / 15))
        return (ratio, 1 - ratio, 0.3)

class TierraVisualSimulation:
    def __init__(self, memory_size=100, initial_population=10):
        self.memory_size = memory_size
        self.memory_width = 100
        self.organisms = []
        self.generation = 0

        for _ in range(initial_population):
            self.organisms.append(Organism())

    def step(self):
        self.generation += 1

        for org in self.organisms:
            org.age += 1
            if random.random() < 0.01:
                org.errors += 1

        offspring = []
        for org in self.organisms:
            if random.random() < 0.3:
                child = org.replicate()
                if child:
                    offspring.append(child)
        self.organisms.extend(offspring)

        while len(self.organisms) > self.memory_size:
            self.organisms.sort(key=lambda o: o.fitness() - o.age * 0.5, reverse=True)
            self.organisms.pop()

    def get_memory_view(self):
        """メモリ空間の可視化用データを生成"""
        memory = np.zeros((10, self.memory_width, 3))
        for org in self.organisms:
            x = org.position % self.memory_width
            y = min(9, len(org.genome) - 3)
            color = org.get_color()
            memory[y, x] = color
        return memory

    def animate(self, steps=200):
        """アニメーション表示"""
        fig, axes = plt.subplots(1, 2, figsize=(12, 4))

        # メモリビュー
        memory_img = axes[0].imshow(self.get_memory_view(), aspect='auto')
        axes[0].set_title('Memory Space (Y=genome size, color=fitness)')
        axes[0].set_xlabel('Memory Position')
        axes[0].set_ylabel('Genome Size')
        axes[0].set_yticks(range(10))
        axes[0].set_yticklabels(range(3, 13))

        # 統計グラフ
        pop_line, = axes[1].plot([], [], 'b-', label='Population')
        size_line, = axes[1].plot([], [], 'g-', label='Avg Genome Size')
        axes[1].set_xlim(0, steps)
        axes[1].set_ylim(0, 120)
        axes[1].set_xlabel('Generation')
        axes[1].legend()
        axes[1].set_title('Evolution Statistics')

        history = {'pop': [], 'size': []}

        def update(frame):
            self.step()

            # メモリビュー更新
            memory_img.set_array(self.get_memory_view())

            # 統計更新
            if self.organisms:
                history['pop'].append(len(self.organisms))
                avg_size = sum(len(o.genome) for o in self.organisms) / len(self.organisms)
                history['size'].append(avg_size * 10)  # スケール調整
            else:
                history['pop'].append(0)
                history['size'].append(0)

            pop_line.set_data(range(len(history['pop'])), history['pop'])
            size_line.set_data(range(len(history['size'])), history['size'])

            axes[0].set_title(f'Memory Space - Gen {self.generation} ({len(self.organisms)} organisms)')

            return memory_img, pop_line, size_line

        anim = FuncAnimation(fig, update, frames=steps, interval=50, blit=True)
        plt.close()
        return HTML(anim.to_jshtml())

# 実行
sim = TierraVisualSimulation(memory_size=80, initial_population=15)
sim.animate(steps=200)

前編まとめ

本記事では、ALIFEの代表的なシミュレーション3つを紹介しました。

シミュレーション	年代	創発される現象
ライフゲーム	1970年	単純なルールから複雑なパターンが生まれる
Boids	1986年	個体の局所的判断から群行動が生まれる
Tierra	1990年	自己複製と淘汰から進化が生まれる

共通して言えるのは、シンプルなルールから複雑な振る舞いが創発されるという点です。
これがALIFEのヤバさであり、何億年という時間繰り返されることで、人類というヤバい発明へと繋がってくるのかもしれません。

＝＞後編へ続く👉

参考文献

• Conway's Game of Life - Wikipedia
• Boids - Craig Reynolds
• Tierra - Tom Ray
• L-system - Wikipedia
• Evolution Gym - MIT