ViTのLayer NormとSoftmaxを量子化する【FQ-ViT】

原論文
FQ-ViT: Post-Training Quantization for Fully Quantized Vision Transformer
https://arxiv.org/pdf/2111.13824.pdf

結論

ViTのLayer NormとSoftmaxを他の量子化とは異なり，工夫して量子化した．

概要

画像認識分野のViTは，大規模で高性能なモデルである．しかし，モデルサイズが大きい場合に，スマホなどの組み込みデバイスに組み込むことが困難になる問題点がある．この大規模なモデルを組み込みデバイス用にモデル圧縮する方法は，様々あるが，その中で，数値をよりコンピュータが計算しやすい低ビットで表現してモデルの圧縮と計算の高速化を実現する量子化を提案する．

具体的に量子化は，通常32や16bitで表現される小数点を含む数値を8や4bitで表現する方法である．しかし，量子化すると数値の持つ表現力が低下して，精度低下する可能性がある．そこで，本論文では，ViTの量子化にあたる精度低下する原因を調査し，改善する．

• ViTの精度低下の原因は，2つある

  • 1つ目，MSAやMLPの前段階で導入されLayer Normalization（LN）の入力にチャンネル間のバラツキがある．LNは全チャンネルを考慮して計算するため，チャンネル間の大きなバラツキは，量子化に大きな誤差を発生させる．これをPower-of-Two Factor (PTF)で解決する

  • 2つ目，softmaxの出力の分布のほとんどの値が，0~00.1間に集中しており，残りのわずかに1に近い値で，かなり歪んだ分布を持つ．このまま，量子化すると誤差が発生する．これをLog-Int-Softmax (LIS)で解決する

これらの方法を組み合わせることで，完全量子化ビジョン変換器の事後学習量子化を実現した最初の研究である．

従来研究

量子化には，モデルの学習後に量子化するPost Training Quantization（PTQ）と学習中に量子化するQuantization-Aware Training (QAT) がある．

• PTQは，学習後のモデルを圧縮して組み込みデバイスに応用できる．また，学習したモデルの数値を変換するだけなので，再学習の必要がなく，簡単に（必要なGPUがいらないで）実装が可能である．本論文で提案する．FQ-ViTは，学習後の量子化である
  $ $
• QATは，学習中に量子化を行うため，学習中に低ビットで計算され，高速に学習可能である．また，最終的に量子化されるモデルを見越して学習しているため，学習後に量子化した際，精度低下に強い可能性を持つ

ViTの量子化では，LNとsoftmaxを量子化すると精度が著しく低下する（Post-Training Quantization for Vision Transformer）．

方法

量子化方法を説明する．

一様量子化

一般的に使用される量子化方法である．本論文で，Cocv，Linear，MatMulモジュールには一様量子化を採用する．

下に一様量子化の式を示す．
clipでは，最低値が0より小さい場合に0へ変換，$s^b-1$より値が大きい場合は，$s^b-1$へ変換する．$b$は表現したいビット数である．8bitで表現したい場合は$b=8$．
式が機能すると，最大値は$s^b-1$に近似して，最小値は0に近似する．

Q(X|b) = \text{clip}\left(\frac{bX}{s} + zp, 0, 2^b - 1\right)

$l$と$u$の式

l = \min(X), \quad u = \max(X)

$s$（量子化スケール）と$zp$（ゼロポイント）の式．

s = \frac{u - l}{2^b - 1}, \quad zp = \text{clip}\left(\frac{b - l}{s}, 0, 2^b - 1\right)

量子化スケールは，値がちょうどよく0から$s^b-1$の範囲に収まるように変換させる．
ゼロポイントは，0の位置を変更させる．例えば，値が100から120の中に集中している場合に，0を0と置いていたら表現幅の無駄遣いなので，100の位置を0として表現して，無駄な表現幅を軽減する．

Log2量子化

LNやSoftmaxに使用される量子化方法である．下に式を示す．

Q(X|b) = \text{sign}(X) \cdot \text{clip}\left(\frac{b - \log_2 |X|}{\max(|X|)}, 0, 2^{b-1} - 1\right)

sign()は，数値が正の場合に1，数値が0の場合に0，数値が負の場合に-1を出力する．

LNの量子化方法

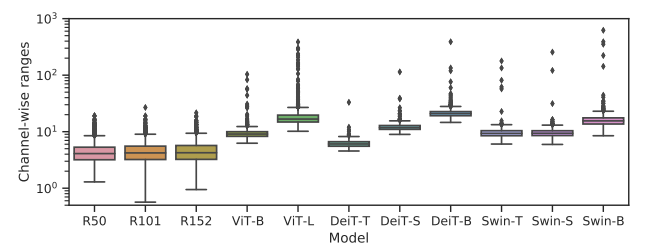
下図では，各モデルのLNの入力に対して，特徴量のチャンネル間のバラツキを示す．ViT系モデル(DeiT，Swin)は，CNN系モデル（ResNet）と比較してバラツキが大きい（ResNetにはLNがないのでLNをつけた）．

LNは全てのチャンネルの値を考慮して計算しているため，このようなバラツキがあると量子化した際に大きな誤差が発生してしまう．
可能な解決策は，グループ単位の量子化，または，チャンネル単位の量子化を使用する方法があるが，これらは小数点のある数値で平均と分散をするため計算が簡略化されない．

• Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT
• Fully Quantized Network for Object Detection

Power-of-Two Factor (PTF)

LNの量子化の問題を解決するPTFを提案する．

量子化方法を以下に示す．

X_Q = Q(X|b) = \text{clip}\left(\frac{bX}{2^\alpha s} + zp, 0, 2^b - 1\right)

量子化シフトの計算方法

s = \frac{\max(X) - \min(X)}{2^b - 1} / 2^K

ゼロポイントの計算方法

zp = \text{clip}\left(\frac{b - \min(X)}{2^K s}, 0, 2^b - 1\right)

各チャンネルで，$a_c$を決定
$a_c$は整数であり，{${{0,1,\dots,K}}$}の中から選択されます．論文ではK=3として，Kは0から3の4通りの整数から量子化誤差が小さくなるように$a_c$が決定されます．
これは，各チャンネルのバラツキを制限するために，チャンネル毎に量子化方法を変化させている．

\alpha_c = \arg\min_{\alpha_c \in \{0,1,\dots,K\}} \left\| X_c - \frac{bX_c}{2^{\alpha_c}s} \cdot 2^{\alpha_c}s \right\|_2

Softmaxの量子化方法

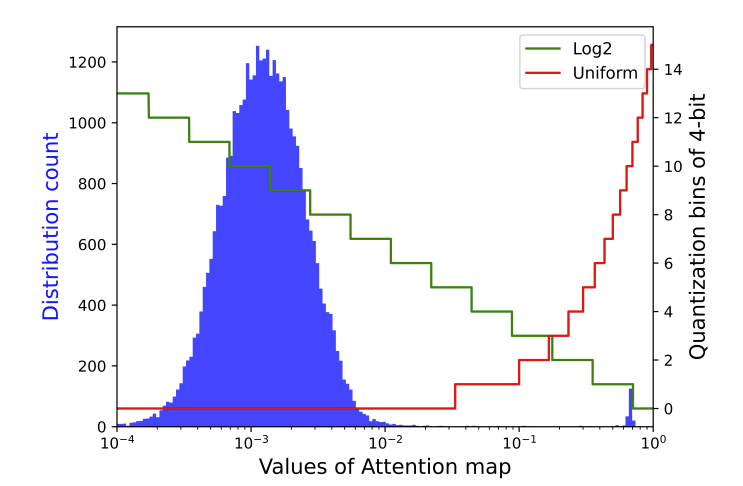
Softmaxは，ViTのSelf-Attention（SA)のQK内積後に導入され，softmaxの出力は，0~1の範囲で値が決定する．そのほとんどの値が，0~00.1間に集中しており，残りのわずかに1に近い値でかなり歪んだ分布を持つ．

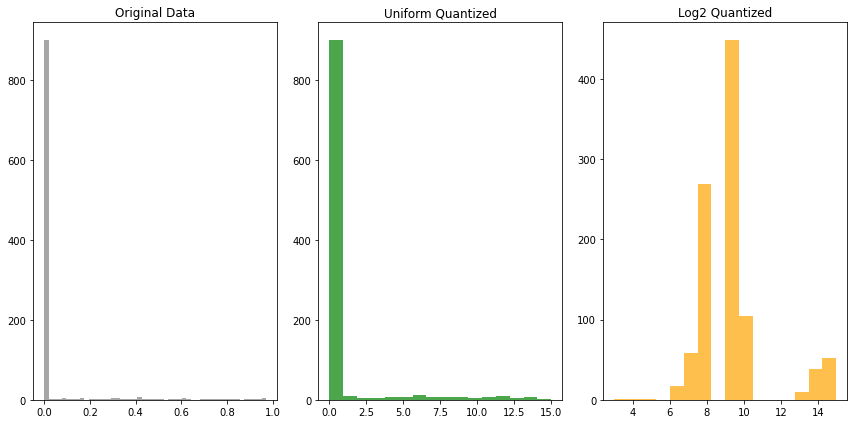
例えば，下図の左のような分布で，ほとんどが0に近似した状態のデータから，中央の一様量子化をした場合に，中央の値の表現力が小さすぎて死んでしまう問題がある．右のlog2量子化は，中央の値を保持する．

また，違う図で表すと，一様分布（赤）では，ほとんどの小さく細かい値を1つの値に量子化している．これは，小さな細かい表現が全て死んでしまう．Log2量子化（緑）は，その問題を多少解決するように量子化する．

Log2の式を以下に示す．
Attnは，SAのQKの内積後の特徴量である．

Q(\text{Attn}|b) = \text{clip}\left(b - \log_2(\text{Attn}), 0, 2^b - 1\right)

また，この量子化で4bitまで圧縮した際に，AttenのVの内積は，BitShiftで計算が可能になる．
BitShiftとは，通常の積和で計算するのではなく，その値をシフトするだけで計算することで，計算効率が向上する．

整数のみの推論

通常のsoftmaxの式

y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)}

新しいsoftmaxに代わる式
sは，量子化スケール．Nは，$2^{b-1}$を示す．

\exp(s \cdot X_Q) \approx s' \cdot \text{i-exp}(X_Q)

\text{LIS}(s \cdot X_Q) = N - \log_2 \left( \frac{\sum \text{i-exp}(X_Q)}{\text{i-exp}(X_Q)} \right)

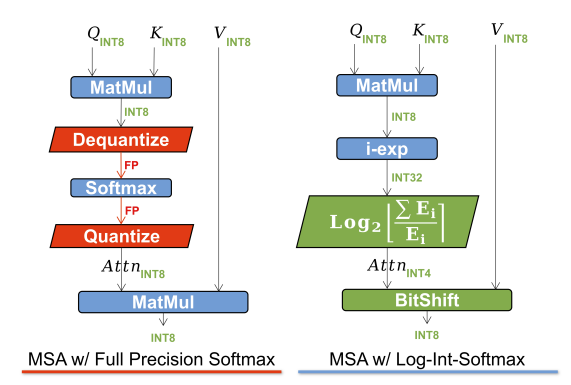
最終的に，下図のような変化がある．
左に通常のSAを示し，右に量子化したSAを示す．QKの内積後，i-expとlog2[・]でsoftmaxを表現．その後Attnでsoftmax後の値を量子化．量子化されたAttnはVとの計算がBitShiftになるので高速!

結果

量子化したViTの性能を比較する．公平な比較のため，重みの量子化はMinMaxに固定する．

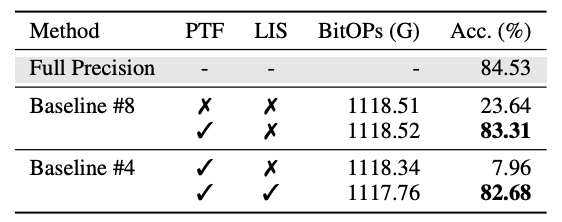
下表に示す．PTFとLISの有無を比較する．
上段に量子化なし，中断に8bit量子化，下段に4bit量子化を示す．PTFとLISの両方を導入した際に，4bitで量子化なしと同等な精度を達成する．

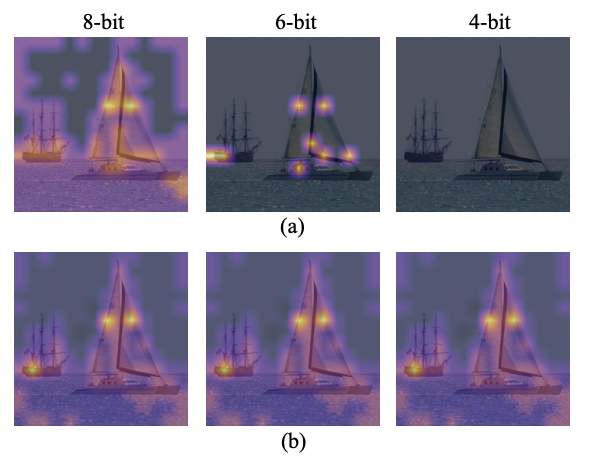
また，上段に示す，通常の量子化の場合は4bitで注目位置を見失ってしまう．これは，値がLNやsoftmaxの影響で死んでしまったことを意味する．下段の論文手法を導入した場合に，可視化の状態は，ほとんど変化しない．

まとめ

今回は，ViTのLayer NormとSoftmaxを量子化する【FQ-ViT】について解説した．ViTのLNとSoftmaxの特性を理解して，それに合った量子化方法を提案する．これにより精度を劣化せずに量子化が可能になる．