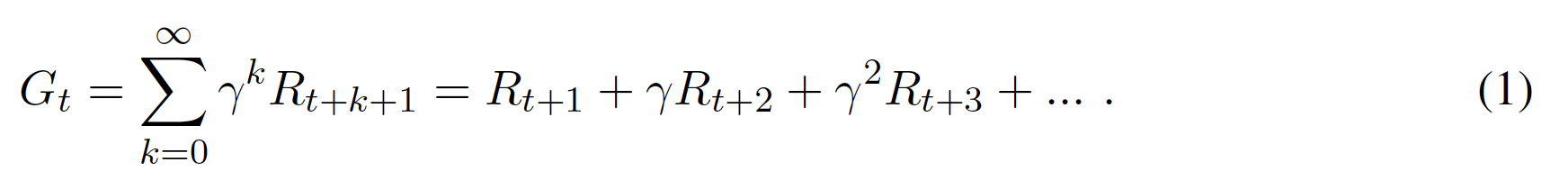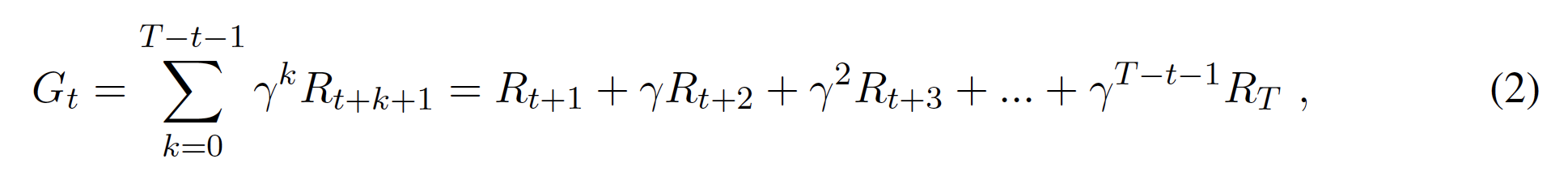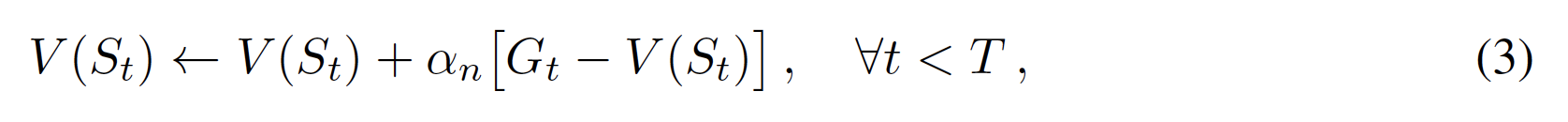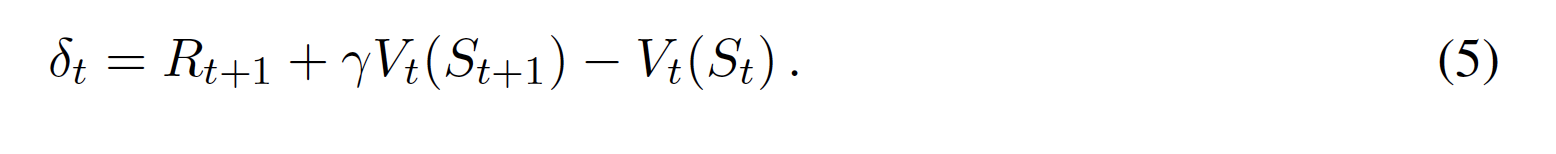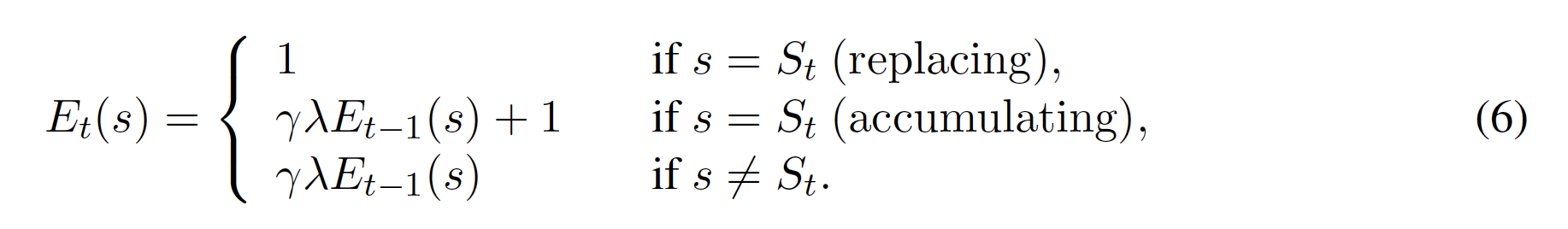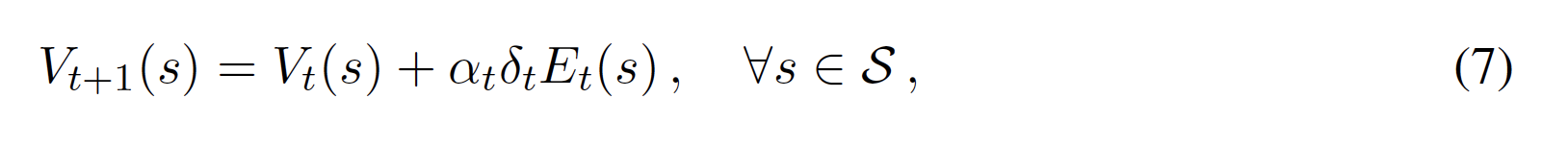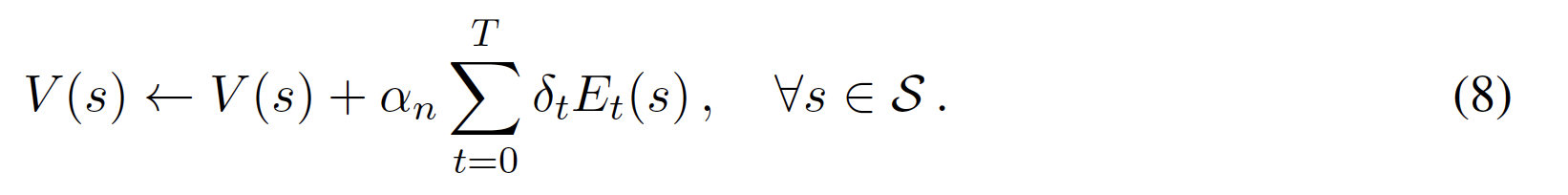Journal of Artificial Intelligence Research 2017
On Monte Carlo Tree Search and Reinforcement Learning
Tom Vodopivec, Spyridon Samothrakis, Branko ˇ Ster
*は注釈(解説)。
<概要>
モンテカルロ木探索(MCTS)は、コンピュータ囲碁での成功をきっかけに、ゲーム業界で広く採用されるようになった。従来の強化学習(RL)手法との関連性については、これまでも説明されてきましたが、木探索におけるRL手法の利用については、まだ十分に検討されていない。
本論文では、この2つの分野の密接な関係を徹底的に再検討し、2つのコミュニティの相互認識を向上させることを目的とする。RLセマンティクスを木探索に単純に適用することで、従来のMCTSがバリエーションの一つに過ぎないような、新しいアルゴリズムが豊富に得られることを示す。RLとオンライン検索を組み合わせた計画手法は、いくつかの古典的なボードゲームやアーケードビデオゲームの大会で有望な結果を示し、最近では我々のアルゴリズムが1位になったことを確認した。本研究は、学習、計画、および探索に関する統一的な見解を示すものである。
<はじめに>
MCTSは、与えられたモデルをサンプリングして最適な決定を見つけるための探索・計画フレームワークとして導入された。その最初の形の一つである木の上側信頼境界(UCT, Kocsis & Szepesva´ri, 2006)は、ゲームをするエージェントにほとんど革命をもたらした。エージェントが内部の*メンタルシミュレーションにアクセスできれば、特に囲碁のゲームにおいて、従来の探索方法と比較してかなりの性能向上を達成することができる。
*メンタルシミュレーション
京都大学大学院 人間・環境学研究科 言語科学 TANAKA YUSUKE氏 2018の論文より、「メンタルシミュレーションとは、世界、身体、心に関する経験の中で獲得した知覚、運動、内省的な状態を再現すること(Barsalou 2008)」
素晴らしい結果を示した後、このアルゴリズムは様々なドメインで広く採用されるようになった。MCTSは単独のアルゴリズムとして開発されたが、その直後に強化学習(RL)との関連性が示唆された。しかし、この関連性は簡単には明らかにならず、ゲームの人工知能(AI)のコミュニティでは広く採用されなかった。この2つの分野の関係は不透明なままで、ほとんどの応用研究者には知らされていなかった。MCTSとRLの手法の関連性について。ゲーム研究者とRL研究者の間に共通の言語が存在しないことが、主な要因の1つである。
この論文では2つのコミュニティが別々に進化した理由を概説し、MCTSとRLの分野のつながりを包括的に分析する。MCTSの観点からゲームAIコミュニティに焦点を当て、2つの分野の類似点と相違点の両方を明らかにする。RL理論を用いてMCTSのメカニズムを徹底的に説明し、伝統的なRL手法では珍しく、それゆえに新規性があると理解されるものを分析する。また、(意図的にも非意図的にも)RLのメカニズムを統合し、RLの用語を使って説明している数多くのMCTSの改良点についても調査している。強化学習の専門家は、この研究の最初の部分を、MCTSの品質のいくつかを理解するのに役立つ拡張された背景と考えるかもしれない。このフレームワークは、MCTSを時間差(TD)学習で一般化したものであると同時に、従来のTD学習法を新しいMCTSコンセプトで拡張したものであると理解できる。本論文では、Sarsa-UCT(λ)と名付けたTDTSアルゴリズムを紹介する。
そのアルゴリズムは、
(1) 表形式の非近似表現で、ドメイン固有の特徴を持たない漸進的に成長する木構造を用いて、ブートストラップ学習法をオリジナルのMCTSフレームワークに適用することに成功した。
(2) *UCB(Upper confidence bounds)選択ポリシー(Auer, Cesa-Bianchi, & Fischer, 2002)と効率的に組み合わせる
(3) このような条件でTDバックアップを評価・分析する。この新しいアルゴリズムは、UCTを適格性トレースのメカニズムで拡張し、新しいパラメータを情報に基づいた値に調整した場合に、その性能を向上させる。さらに、最近では、一般的なビデオゲームAI(GVG-AI)のコンペティション(Perez et al.2015)において、2人対戦のコンペティションで2つの1位を含む素晴らしい結果を達成している
*UCB(upper confidence bounds):行動の選択回数を考慮することで知識活用と探索のバランスを上手く保ち,ε-greedy 手法など
と比べ優れた性能を持つ.コンピュータ囲碁における人工知能 Zen の行動選択にも用いられ(正確には UCBアルゴリズムをベースにした UCT探索を用いている),その強さでよく知られるようになってきている.(参照: 強化学習におけるUCB行動選択手法の効果 2014, 大阪府立大学 斎藤、野津、本田)
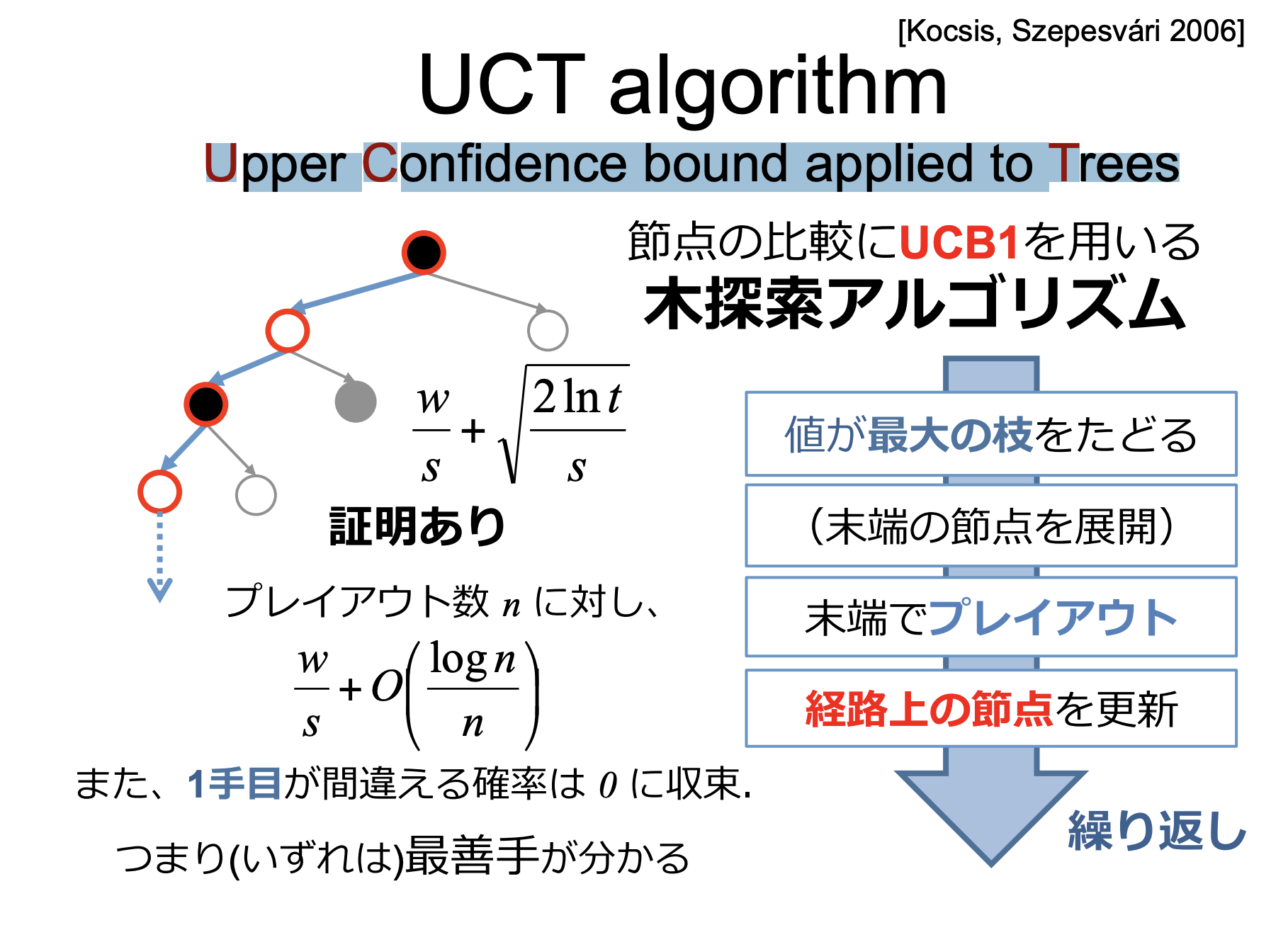
*UCT(Upper Confidence bound applied to Trees) 上記UCBを用いる木探索アルゴリズム [資料:東京工業大学 美添 ⼀樹教授 モンテカルロ木探索の理論と実践2014]
<マルコフ 決定プロセス 以下;MDP>
・状態 s∈Sで、sは一般的な状態、St∈Sは時間tにおける(特定の)状態
・行動 a∈ A aは一般的な行動 At ∈ A (St)は、状態Stで利用可能な行動の中から選択された時間tにおける行動。もし、ある状態に行動がない場合、その状態は終局的である(例えば、ゲームにおけるエンドゲームのポジション)
・遷移確率 p(s' |s, a): 状態sで行動aをとったときに遷移する確率を状態s'で行う。Pr{St+1 = s'|St = s, At = a}となる
.報酬 r(s, a, s' ): 状態sで行動aを取り、状態s'に移動した後の期待報酬。ここでRt+1 = r(St, At, St+1)
・報酬割引率 γ ∈は、後から受け取った報酬の重要性を低下させる
状態に応じて行動を選択する確率を定義するもので、与えられた状況でエージェントがどのように行動するかを定義する。これは、現在の状態から行動への単純なマッピングである場合もあれば、探索プロセスのような複雑なものもあります。MDPを解くには、累積割引報酬を最大化するような方策を見つける必要があり、収益(return)と呼ばれる。
状態(価値)関数vπ(s)は、エージェントが状態sから方策πに従ったときの期待リターンであり、状態行動価値関数qπ(s, a)は、エージェントが状態sで行動aを行い、その後政策πに従ったときの期待リターンである。 MDPと*バンディット問題には明確な関連性があり、後者は「複数状況問題として定式化された場合のプロトタイプMDP」と見なすことができる(Sutton & Barto, 2017)
*バンディット問題:複数のアームと呼ばれる候補から最も良いものを逐次的に探す問題のこと。予測者はいくつかのスロットマシンを与えられ、それぞれのスロットマシンを引くと対応した報酬が得られる。繰り返す試行(アームの選択)を通じて得られる報酬を最大化するのが、予測者の目標である。「参照:人工知能学会、 2016 東京大学 小宮山純平」
MDPのタスクには、一時的なものと継続的なものがあります。一時的なタスクは、限られた長さのシーケンスで構成され、エピソードと呼ばれている。ここでは、1つのエピソードの最終的な時間ステップをTとします。Tは各エピソードに固有のものであることを知っている(すなわち、エピソードの長さは異なるかもしれない)。一方、継続タスクにはエピソードがない(あるいは、T = 1の単一のエピソードを持つと理解できる T = ∞)。 エピソードのある状況で、現在のタイムステップtから最後のタイムステップTまでの収益は
T - t は、エピソード期間のままである。
ディスカウント(γ<1)は、早期に得られた報酬をより重要視し、実際には解への最短経路を優先することになる。これとは別に、ディスカウントは、無限サイズのMDP、サイクルを持つMDP、関数近似を使用する場合に収束性を確保するために必要である。しかし、本稿では、γを1に設定した場合を強調して説明する。これは、実験しているゲームの多くがツリー状の構造(サイクルがない)を持っており、慣習的にγ<1では扱われないからである。ほとんどのゲームでは、勝利を得るために何手必要かは関係ない
<強化学習>
強化学習(RL)は、エージェントが経験から学習するための確立されたパラダイムである(Sutton & Barto, 2017)1998,。RL問題では、エージェントが環境内でアクションを実行し、報酬や環境の現在の状態の観測値の形でフィードバックを受け取る。エージェントの目標は、期待収益(リターン)を最大化すること。エージェントは、環境内でどの行動を行うかを記憶または学習しようとする。
どのような状態がより高い報酬につながるのかを知ることで、将来のより良い行動に役立てるためである。RL問題を定義する方法はいくつかあるが、AI研究ではMDP形式が一般的である。
エージェントはどのような行動を取るべきかを知らされていないため、RL問題は教師付き学習問題よりも難しい。エージェントは、試行錯誤的に状態空間を探索することで、最適な行動を発見することが求められ、また、(自身の)経験(すなわち、環境との相互作用のサンプル)から学ぶことができなければならない。報酬が時間的に遅れている場合は、問題が難しくなる。もう1つの大きな課題は、探索-搾取のジレンマである。エージェントは、過去に高い報酬を得た行動をとるか、あるいは、より良い結果が得られるかもしれない未知の行動を探索するかを決定しなければならない。このジレンマは、MDPやバンディット問題でも中心的な問題である。
一般に、RLの問題は、価値関数を学習し、それを用いて良い政策を設計することで解決できる。このような手法はアクションバリュー法と呼ばれ、ダイナミックプログラミング法、モンテカルロ法、時間差法の3つが代表的である。後者の2つはサンプルベースのRL手法に分類され、*動的計画法とは異なり、環境のモデルを必要とせず、サンプルのインタラクションから学習することができる。本研究では、これらに焦点を当てるが、RL問題は、例えば政策勾配法や進化的アルゴリズムのように、価値関数を明示的に学習することなく、別の方法で解決することも可能である。最先端のRLアルゴリズムについては、Wiering and Otterlo (2012)が紹介している。
*動的計画法: 探索問題を解くための技法の一つ。探索空間中の異なる解が共通の部分問題をもつ場合に、その部分問題の解をメモリー上に蓄えることによって、同じ部分問題が繰り返し解かれないようにすることで効率をあげる。たとえば、東京から福岡までの最短経路を求める際、ある経路の探索の結果、大阪から福岡までの最短経路が得られたとする(部分問題の解)。この場合、別の経路の探索中に大阪に達したら、その後福岡までの最短経路はすでにわかっているので、あらためて計算する必要がない。これが動的計画法の基本的な考え方である。(参照:日本大百科全書(ニッポニカ)
<時間差学習>
TD(Temporal-Difference)学習(Sutton, 1988)は、おそらく最もよく知られたRL手法であり、モンテカルロ(MC)法と動的計画法(DP)を組み合わせたものと理解することができる。MC法のように、環境のモデルを必要とせず、探索空間のサンプリングから経験を得ることができる。DPのように、最終的なフィードバックを受け取るまで待つのではなく、前回の推定値に基づいて状態値の推定値を更新する。これにより、評価の分散が減少し、バイアスが増加するが、通常、学習性能は向上する(Sutton & Barto, 1998)。時間差という言葉は、次の時間ステップにおける状態値の前回の推定値が、現在の時間ステップにおける状態値の現在の推定値に影響を与えるという事実に由来する。
モンテカルロ法では、通常、訪問した各状態St値を、これまでに状態Stを訪問したしたn個のエピソードから集めた収益(リターン)Gの平均値として計算する。インクリメンタル形式に書き換えると、状態値の推定値V (s)は、各エピソードの終わり(t = Tのとき)に次のように更新される。
ここで、更新ステップサイズαn[0, 1]は、ノードへの訪問回数nに応じて減少し、しばしばαn=/1nとなる。 最初のエピソードは、初期状態の値Vinit(s)とn = .1 モンテカルロ法は通常、(Gがすぐには得られないため)値の推定値を更新する前に時間Tまで待たなければならず、オフライン更新を行う。
一方、TD法では、Gtの代わりに予測された状態値Rt+1+γtV(St+1)をターゲットとし、各タイムステップtでオンライン更新を行うことができる。
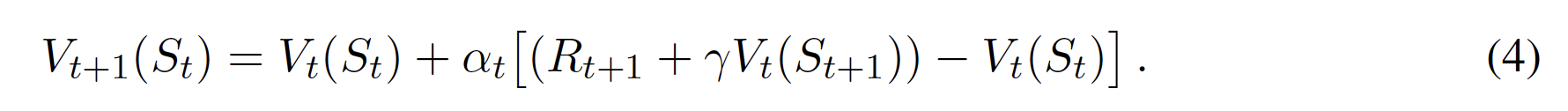
他の推定値に基づいて推定値を更新することをブートストラップといいます。予測された状態値Rt+1+γtV(St+1)と現在の状態値Vt(St)の差をTD誤差δtと呼ぶ。
ターゲットGtとRt+1 + γtV(St+1)の間には、n-ステップリターンと呼ばれる中間的なターゲットを定義することが可能であり、また、それらを様々な方法で組み合わせることができ、その一つがλリターンである(様々な方法で表現可能であり、例えばFairbank and Alonso (2012)を参照)。
同じ問題に別の視点からアプローチすると、(4)のように1つのTDエラーδが最後に訪れた状態の値Vだけをtt更新する必要はなく、複数の(またはすべての)以前に訪れた状態の値を更新するために使用することができると言える。このようなアルゴリズムは、どの状態が以前に訪問されたかを追跡し、どのくらい前に訪問されたかに関して信用、つまり適格性を与える。これは、1ステップのバックアップの代わりに、nステップのバックアップを行うこととして知られており、バックアップされたTDエラーの重みを定義するパラメータは、適格性トレース減衰率λ[0, 1]として知られている。適格性トレースEはメモリ変数であり、各タイムステップですべての状態に対して更新される。更新メカニズムの一般的な2つのバリエーションは、適格性トレースの置き換えと蓄積であり、ここでは
適性トレースを使用することで、各時間ステップ後に状態値を以下のようにオンラインで更新することができる
または、各エピソードの最後にオフラインで
<モンテカルロ木探索とUCTアルゴリズム>
一般に、モンテカルロ木探索(MCTS)アルゴリズムは、強い(ヒューリスティックな)探索手法を用いて、与えられた状況で利用可能な最善の行動を特定する(Browne et al., 2012)。MCTSは、与えられた問題をシミュレーションすることで知識を得るため、少なくともその生成モデル(フォワードモデル、シミュレーションモデル、サンプルモデルとも呼ばれる)を必要とする。MCTSの計画プロセスでは、非対称の探索木を段階的に構築する。
この探索木は、探索的な行動選択ポリシーによって最も有望な方向へと導かれ、反復的に実行される。このプロセスは反復的に実行され、反復回数を増やすことで改善される。MCTSの反復は、通常、4つの連続したフェーズで構成される。(1)木に既に記憶されている行動の選択(ルートからリーフノードへの降下)、(2)新しいノードによる木の拡張、(3)プレイアウト、すなわち、終局状態に達するまでの行動の選択、(4)フィードバックの木へのバックプロパゲーション
ツリーポリシーは選択段階で、デフォルトポリシーはプレイアウト段階で使用される。私たちは、このようなセレクションとプレイアウトの段階で行われる一連のアクションについて、シミュレーションを行う。
MCTSの枠組みは、2006Coulom (2006)がモンテカルロ探索とインクリメンタルな木構造を組み合わせて考案したものである。 同時に、KocsisとSzepesva´ri(2006)は、木構造探索とUCB1選択ポリシー(Auer et al., 2002)を組み合わせ、最初の、そして現在最も人気のあるMCTS手法である木の上層信頼区間(UCT)アルゴリズムを設計した。
MCTSフレームワークに関しては、最初のUCT実装(Kocsis & Szepesva´ri, 2006)では、木のポリシーとしてUCB1選択を、デフォルトのポリシーとしてランダム選択を使用し、各反復において(十分なメモリが利用可能な場合)参照されるすべての状態を記憶し、異なるアクションのシーケンスから到達できる等しい状態(すなわち、転置)を特定し、結果を平均することで評価し、転置表に格納する(すなわち、有向グラフを構築する)(Kocsis, Szepesva´ri, W.)。また,MDPに基づく報酬の割引を考慮し,最終報酬と非最終報酬を区別して,訪問した状態の値をそれぞれ適切なリターンで更新する(すなわち,シミュレーションで訪問した後の報酬の合計で更新する).対照的に,MCTSプラクティショナーは,反復ごとに1つの新しい状態のみを記憶し,転置を識別せず,グラフの代わりに木を構築し,リワードの割引を無視し,末端報酬と非末端報酬を区別せず,最終的な結果(すなわち,シミュレーションにおけるすべての報酬の合計)のみをバックアップし,訪問したすべての状態を同じ値で更新するUCTの変種を広く採用している(Browne et al.,2012).この2つのアルゴリズムを,それぞれオリジナルと標準UCTアルゴリズムと呼ぶ。それぞれのアルゴリズムの擬似コードは,原著論文に記載されている。
UCTの基本的なアルゴリズムは一様乱数のデフォルト・ポリシーを用いているが、強力なMCTSアルゴリズムでは、インフォームド・プレイアウト・ポリシー(事前に知っていることを取り入れたポリシー)を備えていることがほとんどであり、これによりアルゴリズムの性能が大幅に向上する(Browne et al.2012)。また,現在の状態に近い空間をよりよく探索するために,プレイアウトを切り詰める(すなわち,最終状態に到達する前に停止する)こともよく行われる(Lorentz, 2008).最後に、適用されたMCTSアルゴリズムは、多くの場合、ドメイン固有の拡張機能を備えている。一般的な例としては、移動平均サンプリング法(MAST, Finnsson & Bjo¨rnsson, 2008)、全移動優先ヒューリスティック法(AMAF, Gelly & Wang, 2006)、迅速行動値推定法(RAVE, Gelly & Silver, 2011)などがある。
<モンテカルロ木探索と強化学習の関連性について>
最初に、学習、計画、探索に関する異なる視点について議論する。これは、RLコミュニティとサーチ&ゲームコミュニティが別々に発展した理由の一つであろう。次に、MCTS法とRLをプランニングに適用した場合の類似点について説明する。基本的な用語をリンクさせて、多くの仕組みが実際には同じであることを示す。また、基本的な違い、つまり、MCTS法がRLの観点から導入する新しいコンセプトについても調査する。最後に、RLと同様のメカニズムを実装したMCTSの拡張機能を調査する。
学習、計画、検索について
学習法と計画法の間には強い関連性があることが何十年も前から観察されており(Sutton & Barto, 1998)、近年も複数の研究者によって再分析されている(Asmuth & Littman, 2011; Silver, Sutton, & Mu¨ller, 2012; Sutton & Barto, 2017)。どちらのパラダイムも似たような問題を似たようなアプローチで解決しており、どちらも同じ価値関数を推定し、更新して、段階的に推定することができる。
重要な違いは、経験のソースであり、環境との実際のインタラクション(学習)から得られるものか、シミュレーションされたインタラクション(計画)から得られるものかである。このことは、シミュレーション環境に適用すれば、どのような学習方法でもプランニングに使用できることを意味している。その後、MCTSが探索および計画手法とみなされていることから、その探索メカニズムはサンプルベースのRL手法と同等であり、MCTSのフレームワーク全体は計画に適用されるRLと同等である。しかし、このような関係は一見すると明らかではなく、両分野の関係はわずかなものと認識している研究者も少なくない。以下では、この不一致の原因をいくつか提案しますが、同時に、この分野は実際には非常に類似した概念を記述しており、異なる視点から見ているだけであることも主張する。
この2つのコミュニティの視点が異なるのは、(ヒューリスティック)探索法と(強化)学習法の根本的な動機や目標が根本的に異なるからである。MCTSの研究者は、一般的な学習ソリューションにはあまり興味がなく、特定のゲームを特定のアプローチで攻略することに熱心である。ゲームはしばしばエピソード的なものですが、知識(すなわち学習)は通常、エピソードや異なるゲーム間では転送されない。
一方、RLコミュニティでは、より広範なクラスの問題に対して普遍的に適用可能なソリューションを重視しており、その哲学的基盤は、(過剰な)専門家の知識を無原則な方法で使用することを抑制している(ただし、これは実際には非常に効果的であることがわかる)。
一方、RL手法は、得られた知識を更新するための強力な技術を開発することに重点を置き、選択方針にはあまり注意を払わない。この例として、2つのクラスの手法がどのように探索を扱うかが挙げられる。MCTS法は通常、選択ポリシー(UCBポリシーが多い)に任せるのに対し、RL法は楽観的な初期推定値を設定し、それが選択ポリシーを状態空間のあまり訪問されない部分に導くことが多い。このような違いはあるものの、どちらの手法も上記のような共通のタスクを実行する必要がある。つまり、どちらも行動を効率的に選択し、知識を更新し、探索-搾取のジレンマのバランスを取る必要がある
もう一つの大きな理由は、環境のモデルを持っていないというRLの共通の仮定である。強化学習では、サンプルベースの計画シナリオを特殊なケースとして理解している。つまり、学習手法をシミュレーションされた環境に適用することで、モデルが必要になるのです。とはいえ、完全なモデルが必要なわけではなく、(MCTSのように)近似的または生成的なモデルがあれば十分かもしれない。また、モデルが与えられていなくても、手法がオンラインで学習する(つまり、遷移確率を追跡する)こともできる。最近のRLにインスパイアされた研究では、MCTSのようなアルゴリズムが、シミュレーションされていない経験に対してもそのような方法で適用できることが確認されている(セクション5.3)。さらに、生成モデルが利用可能な従来のMCTSにおいても、モデルは必ずしも完全ではなく、非常に確率的であったり、環境の一部しかシミュレートしていなかったり(2015,例えば、GVG-AI競技会のように)、通常は遷移確率を開示しておらず、タスクに関与する他のエージェントの動きをシミュレートしていないこともある。例えば、マルチプレイヤーゲームでは、他のプレイヤーは容易に予測できない環境の一部として理解され、むしろ別個にモデル化されることが多い。
以上をまとめると、MCTS法もRL法と同様にモデル関連に対処する必要がある。探索手法では、ほとんどのゲームがそのような性質を持っていることから、決定に基づいて木構造を構築することが多く、状態観測可能性は転置テーブルを使用することができるボーナスと考えられている。一方、RLでは、状態の観測が可能であることは当然のことと考えられている(そうでなければMDPのMarkov特性は成立しません)。RLの研究では、より一般的な、完全に連結された状態のグラフに焦点を当てている。
実際には、グラフが明示的に表現されることはほとんどなく、より単純なMDP解法では表形式の表現(転置表と同じ)が用いられ、ほとんどのRL法では関数近似技術が用いられている。このような表現方法の違いにもかかわらず、探索手法もRL手法も、得られた知識を一般化し、状態空間の関連する部分に移すことを目指している。MCTSとRLを連携させる際、Baier(2015)は、知識を共有する(同じ推定値で表される)状態空間の部分に対して「neighbourhoods」という概念を用いている。MCTSでは、近傍領域は通常、専門家の知識やヒューリスティックな基準に従って状態をグループ化する特定の拡張機能(2006,例えばAMAF、Gelly & Wangなど)によって定義されるのに対し、RLでは、関数近似に使用される特徴(実際には、これも専門家の知識に従って選択されることが多いが、例えばダイレクトボードの画像のように非常に自然なものであることも多い)によって定義される。
最後に、ゲームと検索のコミュニティは、囲碁のゲームで素早く成功したことから、MCTSを検索技術として採用した(Gelly, Wang, Munos, & Teytaud, 2006)。オリジナルのUCTアルゴリズム(Kocsis & Szepesva´ri, 2006)は、MDP(セクション2.4)を用いて設計・分析されていたが、MDP(セクション2.1)やRL法に不可欠な報酬の割引を無視した改良版が採用された。
以上のことから、MCTS分野とRL分野の間には共通言語が存在しないと考えられます。その結果、異なる視点からではあるが、似たようなコンセプトで多くの研究が行われてきた。この相互認識を改善することは、両方のコミュニティにとって有益である。次のセクションでは、この目標に向けて一歩を踏み出し、モンテカルロ・サンプリングを用いたRL手法をMCTS手法の一般化としてどのように理解できるかを説明する。
<次回へ続く!>