この記事は理情 Advent Calendar 2025の16日目の記事です。
よかったら、他の記事も読んでくださると幸いです。
tl; dr
- MinCaml to Brainfuckトランスコンパイラを作ったよ
- CPS変換 + Lambda Lifting + Defunctionalizationでスタックマシンで実行できる形式にすることで達成したよ
- Brainfuckでランダムアクセスメモリーを再現した方がおそらく簡単だけど、今回は縛ったよ
- 現在のAIでも、コンパイラを独立して書くこととesolangを書くことはできないっぽいよ
- 期限が決まっているタイプのアドカレみたいな記事では、あらかじめ見通しを立ててない限り難しすぎるトピックに挑戦するべきタイミングではないよ
はじめに
理学部情報科学科には「CPU実験」という名物授業(実験)があります。
この実験では、初めの授業で「このレイトレを動かせる様なコンピュータを作ってきてくれ」と野に放たれ、好き勝手にCPU作成に悪戦苦闘するものとなっています。
班員は基本的に4人で構成され、ほとんどの班が「コア係」、「メモリ・FPU係」、「シミュレータ係」、「コンパイラ係」に役割を分担します。
詳しい説明は本題とは逸れてしまうため、割愛しますが、コンパイラ係であるYutchyがふと「MinCamlをBrainfuckにコンパイルできたら楽しいんじゃね?」と思って軽い気持ちで作成し始めた記事です。
結論から言うと、Brainfuckを舐めすぎていました。1:
今回の目標
Ocamlのサブセットであり、仕様のサイズが小さい関数型言語であるMinCaml(のさらにサブセット)を、かの有名なesolangであるBrainfuckにコンパイルするトランスコンパイラの作成を目標とします。
部分関数を返す様な関数など、関数自体をオブジェクトとして扱うコードは未検証です。
また、入出力が現状未対応です。
具体的なレギュレーション
- コンパイルするMinCamlにはFloat, Tuple, Arrayが含まれないものとする
- Brainfuckの仕様は想定される最も厳しいものを想定します。2
- 各cellは127以下の非負整数値しか入れることができず、オーバーフローした時の処理は未定義
- 0より小さいポインタにアクセスするのは未定義
- テープ長は無制限とする3
- コンパイラはなるべくBrainfuckでランダムアクセスメモリをシミュレートしないようにする
- これをすると普通に実行をシミュレートするだけで、あまり面白くないので
前提知識
前提としてMinCaml言語4とBrainfuckについて軽い紹介と、MinCaml処理系で既に行われている処理について軽く紹介します。
MinCaml言語
関数型言語であるOcamlのサブセットです。
以下のような見た目をしています。
let x = 42 in (* 変数 *)
let rec f x y = x + y in (* 関数定義 *)
let rec g x = (* 再帰関数も表現できる *)
if x = 0 then 0
else x + g (x - 1)
in
let k = 57 in
let y =
let t = g 1 in t + k in (* nested-letと外部変数; y = 58 *)
print_int (f y x) (* 100 *)
この記事を読む上では、
-
let ... inで変数定義 -
let rec f args = ... inで関数定義 -
if ... then ... else ...で条件分岐
であることを理解していれば問題ありません。
その他MinCamlに含まれないOcamlの仕様として、
let partial_f =
(let rec f x y = x + y in f 42) (* 部分適用 *)
in
let x = partial_f 57 in (* x = 99 *)
let y = (fun x -> x + 42) 57 (* 無名関数、y = 99 *)
- 引数が十分与えられてない時は、与えられた分の引数のみ評価する
- 無名関数は
fun args -> ...の様に書く
ことを把握していただけると、記事の理解がスムーズになると思います。5
詳しいMinCaml言語の仕様はMinCamlの構文と型を参照してください。
Brainfuck
+-><[].,のみからなる非常に使用サイズが小さい難解プログラミング言語(esolang)です。
上記の文字以外はコメントとして無視されます。
実行時には整数が書き込める十分長いテープと、その番地を指すポインタが存在します。
テープは初めに0クリア、ポインタは0に初期化され、あとは以下に従ってプログラムを実行します。
| 記号 | 意味 |
|---|---|
+ |
ポインタの指している番地に1を足す |
- |
ポインタの指している番地に1を引く |
> |
ポインタを1つ正の向きに動かす |
< |
ポインタを1つ負の向きに動かす |
[ |
ポインタの指している番地の値が0なら次の]の次まで実行をスキップする |
] |
前の[まで戻る |
, |
入力を1byte分読む |
. |
ポインタの指している値に対応するASCII文字を出力する |
言語仕様は非常にシンプルであるため、esolangの中ではかなり素直な部類ではあります。
しかし、特にループ[]が指しているポインタの値に依存しているため、ランダムアクセスが非常に難しいという問題があります。
今回はこれを全力で回避していきます。6
MinCaml処理系
MinCaml処理系の最適化部分以外 + 独自で実装した7A正規化までを前処理として使います。
具体的には、
- 式のパース
- 型検査
- K正規化
- A正規化
- クロージャ変換8
を行なっています。
といっても、普段からコンパイラを書かない方々にはなんのこっちゃだと思うので、重要な部分のみ軽く説明します。
K正規化
ネストした式をなくすための正規化です。
let x =
let y = 42 in
y + 57 + 1
は、K正規化によって
let x =
let y = 42 in
let t1 = y + 57 in (* 一時変数を使ってネストした式を分割! *)
t1 + 1
の様に変換されます。
ここではネストされたletは解消されません。
ところで、K正規化は、ML Kitというコンパイラに由来しており、あまり一般名ではない様です。
A正規化
ネストしたletをなくすための処理です。
let x =
let y = 42 in
let t1 = y + 57 in (* 一時変数を使ってネストした式を分割! *)
t1 + 1
は、A正規化によって
let y = 42 in
let t1 = y + 57 in
let x = t1 + 1
の様に変換されます。ずいぶん読みやすくなりますね。
コンパイラを書く際もA正規化すると場合分けが減るので、雑に適用しておいています。
本題
本題のMinCaml to Brainfuck コンパイラで実装した部分を見ていきます。
バックエンド
コンパイラを作る際は低レイヤー側から考えると良いらしいので、低レイヤー側から考えます。9
今回ゴールとするBrainfuckのコードは以下の様にし、
+>+<[>[block1]>[block2]>[block3]>…[block_n]<<<…<<<]
テープの構造を以下の様にします。
[blockactivator...][registers...][variables...][stack...]
といってもさっぱりだと思うので、詳しく解説していきます。
Brainfuckのコードは、疑似コードで書くと次の様な感じです。
mem[0] = 1
mem[1] = 1
while (mem[0]){
if (mem[1]){
// block1...
}
if (mem[2]){
// block2...
}
...
}
のようなコードになっています。関数やif内の処理を分割することでblock間を飛ぶ様に処理ができます。
この様なコードを"Trampoline"というらしいです。10
ここでの問題は、関数のリターンが活用できないことと、外部変数をどのように扱うかが問題です。
この問題は一度さておくとして、次はメモリを見ていきましょう。
[block_activator...][registers...][variables...][stack...]
において、
| ブロック名 | 内容 |
|---|---|
| block activator | ブロックに入るためのmem[1], mem[2], ...を管理するための領域です。blockの数をBとして、O(B)の領域が必要です。11 |
| registers | 途中計算を保存するための領域です。128bitを確保しています。 |
| variables | 変数を保存するための領域です。変数の数をNとして、O(N)の領域の確保が必要です。 |
| stack | スタック領域です。純粋なLIFOスタックはランダムアクセスメモリよりかなり実装が楽です。引数や外部変数は全てここで制御します。 |
また、テープには127以下の数字しか入れることができないため、32個のcellをまとめて一つの整数を表現しています。これによって加算や値のコピーにかかる定数倍が32に抑えられるので、かなり嬉しいです。
CPS変換
Brainfuckには制御構文が[]しかないため、関数のreturnを表現するのは難しいです。
逆転の発想として、そもそも関数のreturnをなくせないでしょうか?
これは「CPS変換」と呼ばれる方法によって、達成できます。
CPS変換は、関数の呼び出しに継続、すなわちその後の処理を入れ込んだ関数を明示的に渡し続けることで末尾再帰の形を作り出し、結果的にreturnが不要になります。
ここからは具体例として、次のコード12を使用します。
let k = 42 in
let rec fib_alt n =
if n <= 1 then n
else
let t = fib_alt (n - 1) + fib_alt (n - 2) + k in
t + t
in
print_int (fib_alt 5)
これをCPS変換すると、
let k = 42 in
let rec fib_alt n cont =
if n <= 1 then cont n
else
fib_alt (n - 1) (fun x ->
fib_alt (n - 2) (fun y ->
let t = x + y + k in
t + t
)
)
in
fib_alt 5 (fun x -> print_int x)
の様になります。
ぱっと見だと複雑ですが、最後の呼び出し、fib_alt 5 (fun x -> print_int x)を見ればなんとなく意味がわかるのではないでしょうか?
これはつまり、fib_altを読んだあとは、その数をprintしてね、というのを関数の引数として明示的に渡しています。
MinCamlには無名関数が存在しないので、これを解消すると、
let k = 42 in
let rec fib_alt n cont =
if n <= 1 then cont n
else
let g x =
let h y =
let t = x + y + k in
cont (t + t)
in
fib_alt (n - 2) h
in
fib_alt (n - 1) g
in
let rec print x = print_int x in
fib_alt 5 print
の様になります。
Lambda Lifting
先のコードは継続を明示的に指定できてはいますが関数内に関数が存在しています。
そのため、外部で定義されている変数が存在し、厄介です。
これを解消するための一つの方法がLambda Liftingです。
これは、外部変数を全て明示的に引数に含む様にするための処理です。
もし関数に外部変数が存在しなければそのまま関数をトップレベルまで引き上げることができます。
まず先のfib_alt_cpsedの外部変数をなくすと、
let k = 42 in
let rec fib_alt k n cont =
if n <= 1 then cont n
else
let g n k fib_alt cont x =
let h k x cont y =
let t = x + y + k in
cont (t + t)
in
fib_alt k (n - 2) (h k x cont)
in
fib_alt k (n - 1) (g n k fib_alt cont)
in
let rec print x = print_int x in
fib_alt k 5 print
となり、関数をトップレベルまで引き上げると、
let h k x cont y =
let t = x + y + k in
cont (t + t)
in
let g n k fib_alt cont x =
fib_alt k (n - 2) (h k x cont)
in
let k = 42 in
let rec fib_alt k n cont =
if n <= 1 then cont n
else fib_alt k (n - 1) (g n k fib_alt cont)
in
let rec print x = print_int x in
fib_alt k 5 print
とまで変換できます。(どうしても部分適用が含まれてしまう点に注意が必要です。)
これでTrampolineの形にかなり近づいたのではないでしょうか?
defunctionalization / Trampoline
fib_alt_lambda_lifted.mlの関数になっている部分を全てlabelによるジャンプに書き換えます。
ここで重要な事実として、CPS変換されており、継続が最後の段階でしか呼ばれていないプログラム(Linear Continuation)は純スタックマシンによって実行可能であることです。
これは継続以外の関数は明示的にスタックに積み、継続はスタックの残りを用いて処理を行う様にすると達成されます。
例えば、
let h k x cont y =
let t = x + y + k in
cont (t + t)
in
let g n k fib_alt cont x =
fib_alt k (n - 2) (h k x cont)
in
let k = 42 in
let rec fib_alt k n cont =
if n <= 1 then cont n
else fib_alt k (n - 1) (g n k fib_alt cont)
in
let rec print x = print_int x in
fib_alt k 5 print
は、上側をスタックの末尾として、
fib_alt 5:
fib_alt
n = 5
k = 42
print
==================================================================
fib_alt 4:
fib_alt
n = 4
g
n = 5
k = 42
fib_alt
print
==================================================================
...
==================================================================
fib_alt: n = 1
g
n = 2
k = 42
fib_alt
g
...
g
n = 5
k = 42
fib_alt
print
==================================================================
g: x = 1, n = 2
fib_alt
n = 0
h
k = 42
x = 1
g
...
g
n = 5
k = 42
fib_alt
print
==================================================================
...
==================================================================
h: x = 1, y = 0, t + t = 86
g
n = 3
...
g
n = 5
k = 42
fib_alt
print
==================================================================
g: x = 86, n = 3
fib_alt
n = 1
h
n = 2
k = 42
x = 1
g
...
g
n = 5
k = 42
fib_alt
print
==================================================================
...
==================================================================
h: x = 86, y = 1, t + t = 258
g
n = 4
k = 42
fib_alt
g
n = 5
k = 42
fib_alt
print
のように実行すれば良いです。
ここで賢いのは、例えば最後のh: x = 86, y = 1, t + t = 258の時、
g
n = 4
k = 42
fib_alt
g ======= ここから全部継続cont
n = 5 |
k = 42 |
fib_alt |
print |
上図のように継続を部分適応部分の最後におくことで、スタックの下側を自然にcontとしている点です。これは継続を1度のみ使うLiniar Continuationの強みで、これによってスタックマシンによる再帰の実行が可能となります。
これを踏まえて関数の変換を行うと、
let h k x cont y =
let t = x + y + k in
cont (t + t)
in
let g n k fib_alt cont x =
fib_alt k (n - 2) (h k x cont)
in
let k = 42 in
let rec fib_alt k n cont =
if n <= 1 then cont n
else fib_alt k (n - 1) (g n k fib_alt cont)
in
let rec print x = print_int x in
fib_alt k 5 print
は、
h:
y = pop()
cont = pop()
x = pop()
k = pop()
t = x + y + k
push(t + t)
jump(cont)
g:
x = pop()
cont = pop()
fib_alt = pop()
k = pop()
n = pop()
push(cont)
push(x)
push(k)
push(h)
push(n - 2)
jump("fib_alt")
fib_alt:
cont = pop()
n = pop()
k = pop()
if n <= 1 then jump("if_fib_alt")
else jump("else_fib_alt")
if_fib_alt:
push(n)
jump(cont)
else_fib_alt:
push(cont)
push("fib_alt")
push(k)
push(n)
push("g")
push(n - 1)
jump("fib_alt")
print:
x = pop()
print_int x
Halt
main:
k = 42
push("print")
push(5)
push(k)
jump("fib_alt")
のように、非常にシンプルな形で記述できました。13
その後
あとはBrainfuckでそれぞれの命令を記述するだけです!
頑張りましょう!14
あとがき
Brainfuckトランスコンパイラと言いながら、ランダムアクセスメモリを縛ったことで、実質的にスタックマシンへのコンパイルが主になりました。自分はdcも好んで使っているので、もしかしたらスタックマシンが好きなのかもしれません。
さて、あとがきを書いている時点(12月16日の昼間)でも、まだ実装が終わっていません。
アドカレの記事を書くときには、まずちゃんと工数を見積もってからプロジェクトを決めましょう。15
当初は5時間くらいでできるかなぁと思ったプロジェクトに50時間以上かかっています。
この記事でやったことはCPU実験における「余興」に当たります。
余興のせいで本編を蔑ろにしてしまったのですが、一応色々な最適化手法に触れることができたり、メモリの配置について詳しくなったりしたので、班員の皆さん許してください。
ここまでお読みいただきありがとうございます。
作成したものがこちらになります
シミュレータの動作ですが、無事fib_altで2144が計算されたことが確認できます。1617
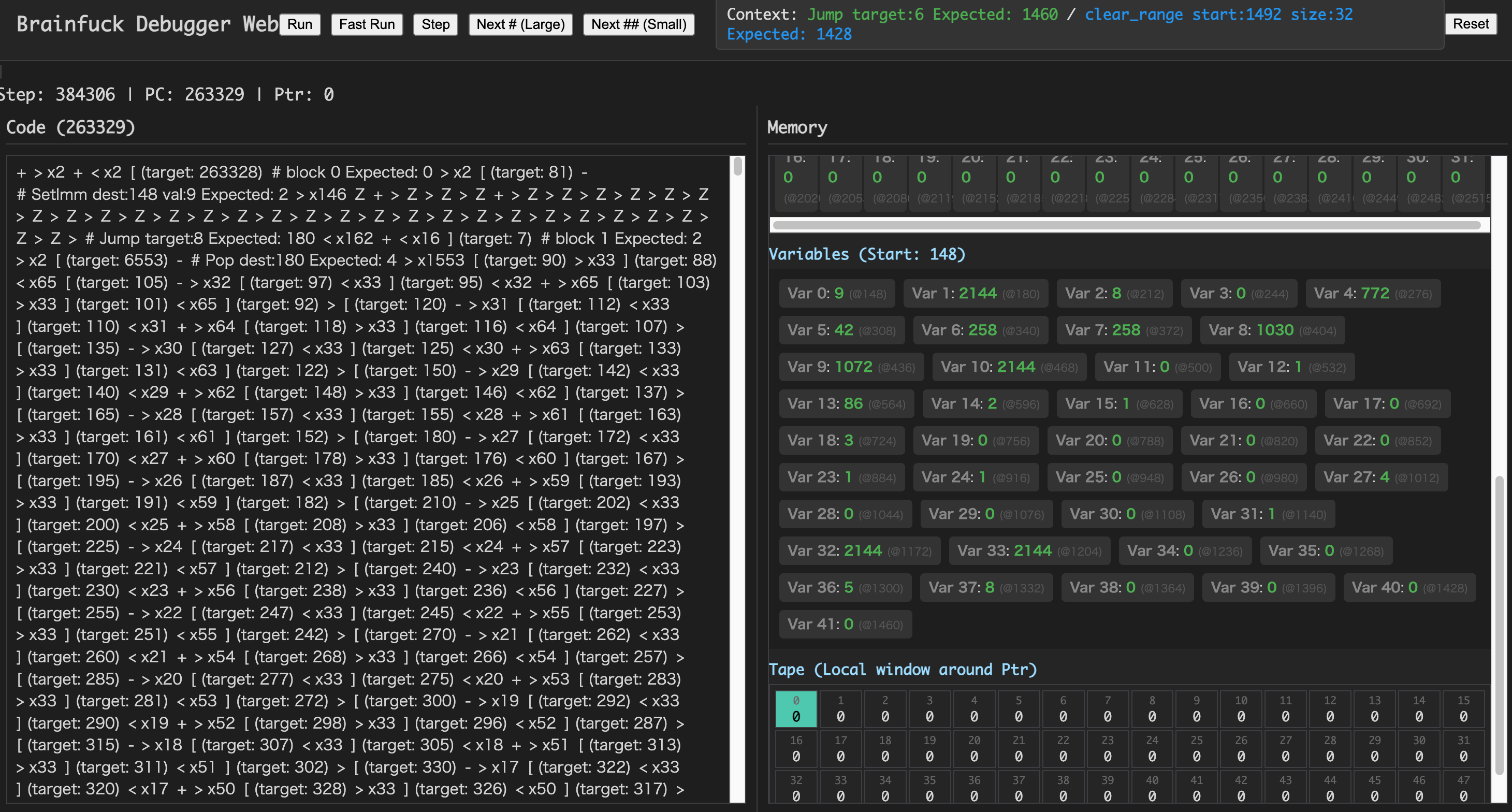
サンプルコードは膨大(~数十MB)なので、githubの方からご覧ください。
最後に
このプロジェクトを始めてから体感50%くらいでBrainfuckの悪夢を見る様になりました、助けてください
-
なんとこれを書いている12月15日現在、いまだにコンパイラのデバッグが終わっていません ↩
-
コンパイラで生成されたコードが環境依存していると嫌なので ↩
-
そうでないとチューリング完全でないので甘めに無制限としています。なおある程度のコードはテープ長30000以下でおさまります。 ↩
-
MinCamlがOcamlのサブセット言語としての呼び名と、MinCaml処理系としての呼び名でオーバーロードされているため、誤解が生じる際は以下MinCaml言語とMinCaml処理系と書き分けます。 ↩
-
最適化途中の疑似コードとして使用する機会があるので ↩
-
おそらくランダムアクセスを全力で回避するより、ランダムアクセスを実装した方が間違いなく簡単です。今回は面白さのために全力で回避します。 ↩
-
最適化パイプラインにもassoc.mlが存在して、A変換を行なっていますが、これは最適化パイプライン内なので改めて書いています。 ↩
-
後でLambda Liftingを行うのであまり重要ではなく、割愛します。 ↩
-
参考文献:アドカレ1日目記事、読んでね ↩
-
思いついたものには大体名前がついているものですね ↩
-
ランダムアクセスのために2Bの領域を確保しています ↩
-
2144を出力するコードです。 ↩
-
簡単のために多少の実行順序の変更を行なっています。 ↩
-
頑張りました ↩
-
理論が間違っていて、工数を見間違えたのが原因ではありましたが... ↩
-
printなどは力尽きたので後日... ↩
-
12月16日21時44分に実装完了しました ↩