はじめに
みなさん(特に業務で推薦システムの構築に関わっている方)は普段どのようにして, 推薦アルゴリズムの性能を評価しているでしょうか?よく使われる評価指標として, MSEやMAE, AUCなど色々挙げられると思います. 実は, それらの評価指標をそのまま使ってしまうと間違った性能評価をしてしまい兼ねません. また, 多くの人がその事実に気づかぬまま間違った性能評価を信じてしまっている可能性があります.
間違った性能評価をしてしまうのはどうしてなのか? それはどのように補正すれば良いのか?をなるべくわかりやすく解説したつもりなので, 推薦システムの評価について考え直すきっかけにしていただけたら嬉しいです.
目次
- Toy Example
- 問題の原因を特定する
- IPSによるBias除去
- 簡易実験
- 最後に
- 参考
Toy Example
問題のイメージを持っていただくために, 簡単な推薦評価の例を用います.
今, Horror Lovers・Romance Loversというユーザー属性とHorror・Rommance・Dramaという3つのジャンルのみが存在するシンプルな映画推薦の系を考えます. さらに各ユーザーがそれぞれの映画に対して付すRatingがユーザー属性と映画ジャンルの組み合わせのみによって決まる(つまりRatingの付き方は高々6通り)とします. この時, 予測1($\hat{Y}_1$(と予測2($\hat{Y}_2$)(例えば予測1は, Horror LoversがRomance映画に対してRating 1を予測するという見方です)の性能を自分たちが所持している推薦ログデータからMAEを用いて評価したいとします.

ここで重要なのが評価に用いるログデータの生成過程です. この例では, ログデータが右上の過去の推薦方策と名付けられている行列のように各ユーザー属性と映画ジャンルの組み合わせごとに異なる推薦確率を持った方策によって集められたログデータであるとします. これにより, 例えば3200個のRatingが含まれるログデータについては各ユーザーと映画ジャンルの観測回数は図のようになり, 要素ごとの観測回数がかなり異なることがわかります. この観測回数の不均衡はひとえにこのデータが各ユーザー属性と映画ジャンルの組み合わせごとに異なる推薦確率を持った方策によって集められたことに起因します.

このような各要素ごとに観測回数(生成確率)が一様ではないデータを推薦システムの評価に使ってしまうと図のように, 真の性能は予測1の方が良い(MAE = 0.33)にも関わらず, ログデータ上で計算されたMAEは予測2の方が良くなってしまうという非常に厄介な問題が生じます. では, どうしてこのような厄介な問題が生じてしまうのでしょうか?
問題の原因を特定する
前章の例で見た問題の原因を探るために,推薦システムの評価の問題を定式化します.
今各ユーザーを$u \in \{ 1, .., U \} = \mathcal U$, 各アイテムを$i \in \{1, ..., I \}=\mathcal I$と表します. また, $Y_{u,i}$をユーザー$u$がアイテム$i$に対して有する真のRating, $\hat{Y}_{u,i}$をそれに対する予測値とします. 私たちが達成したいのは, 予測値の集合 $ \hat {Y} = \{ \hat {Y}_{u, i} \}_{ (u,i) \mathcal U \times \mathcal I } $の性能を正確に評価することです.
予測値集合$\hat Y$を評価するためには, 何らかの評価指標が必要ですのでそれを$\delta \left( Y_{u,i}, \hat{Y}_{u,i} \right)$としておきます. $\delta$は真のRatingとそれに対する予測値を入力とする関数で, 例えばMSEを評価指標とするなら$\delta(x, y) = (x - y)^2$です. この評価指標$\delta$のもとでの$\hat{Y}$の真の性能を次のように定義します.
\begin{aligned}
R \left( \hat Y \right) = \frac{1}{U \cdot I} \sum_{u, i} \delta \left( Y_{u,i}, \hat{Y}_{u,i} \right)
\end{aligned}
単に全てのユーザーとアイテムのペアについて評価関数$\delta$の平均を取っているだけです. しかし, 私たちは全てのユーザーとアイテムのペアについて真のRatingを知ることはできないので, この真の評価値を知ることもまた不可能です. よって, 自分たちが観測してすでにRatingを知っているデータだけを使って$R \left(\hat{Y} \right)$を推定したいというモチベーションが自然と湧き上がります.
ここで自分たちが観測しているRatingと観測していないそれを区別するために, Observation(観測)の頭文字を取って新たな変数$O$を導入します. この$O$は2値確率変数であり各ユーザーとアイテムのペアに対応して独立に存在します. $O_{u,i} = 1$ならば, ユーザー$u$とアイテム$i$のペアについてのRatingを観測していることを意味し, $O_{u,i} = 0$ならば, そのペアについてのRatingを私たちが観測していないことを意味します. また, $O_{u,i}$の期待値 $ \mathbb{E} \left[ O_{u,i} \right] $は, $u$が$i$に対して有する真のRating $Y_{u,i}$が観測される確率を意味します.
この確率変数$O_{u,i}$を用いると真の評価値$R \left(\hat{Y} \right)$に対するNaiveな推定量(そしておそらく多くの方が性能評価に用いている推定量)を次のように書き下すことができます.
\begin{aligned}
\hat{R}_{Naive} \left( \hat{Y} \right) = \frac{1}{ \sum_{u, i} O_{u, i} } \sum_{(u,i): O_{u,i} = 1} \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right)
\end{aligned}
この式では, $O_{u,i} = 1$つまり, 自分たちがログデータとして観測しているRatingとそれに対する予測値の誤差の平均を取っています. 予測値集合$\hat{Y}$の評価の仕方としてごく自然な方法だと思います. しかし, $Y_{u,i}$が観測される確率が一様ではない場合, このNaive推定量$\hat{R}_{Naive}$が真の評価値$R$に対してBiasを持つということを次のように理論的に示すことができます. (証明については読み飛ばしても問題ないです.)
今分母の$\sum_{u, i} O_{u, i} $を任意の正の定数$N$で置き換えた上で, $\hat{R}_{Naive}$の確率変数$O$についての期待値をとります.
\begin{aligned}
\mathbb{E}_O \left[ \hat{R}_{Naive} \left( \hat{Y} \right) \right] & = \mathbb{E}_O \left[ \frac{1}{ N } \sum_{(u,i): O_{u,i} = 1} \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right) \right] \\
& = \mathbb{E}_O \left[ \frac{1}{ N } \sum_{u,i} O_{u,i} \cdot \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right) \right] \\
& = \sum_{u,i} \frac{\mathbb{E}_{O_{u,i}} \left[ O_{u,i} \right]} {N} \cdot \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right)
\end{aligned}
ここで, $\hat{R}_{Naive}\left( \hat{Y} \right) = R\left( \hat{Y} \right)$が成り立つためには, 任意の$u$と$i$ついて$\frac{\mathbb{E}_{O_{u,i}} \left[ O_{u,i} \right]} {N} = \frac{1}{U \cdot I} $が成り立つ必要がありますが, 観測確率が一様ではない場合, この条件を満たす定数$N$は存在しません. よって, $\hat{R}_{Naive}\left( \hat{Y} \right) \neq R\left( \hat{Y} \right)$であり, Naive推定量は真の評価値に対してBiasを持つことがわかりました. また, そのBiasは観測確率が一様ではないことに起因することも示唆されました.
もしもみなさんがNaive推定量と同様の方法で推薦システムの評価をしていたら, その評価はBiasを持っているため信頼できる指標ではなかったということになります.
IPSによるBias除去
前章では, Naiveな推定量がBiasを持ってしまうという悲しい事実を紹介しましたが, IPS (Inverse Propensity Score)と呼ばれる方法でBiasの除去が可能です. ここで, Propensity Score (傾向スコア) とは$u$が$i$に対して有する真のRating $Y_{u,i}$が観測される確率$ \mathbb{E} \left[ O_{u,i} \right] $のことです. 表記の簡略化のため, 傾向スコアを$P_{u,i} = \mathbb{E} \left[ O_{u,i} \right]$と置くと, IPSを用いた推定量$\hat{R}_{IPS} \left( \hat{Y} \right)$は, 次のように定義されます.
\begin{aligned}
\hat{R}_{IPS} \left( \hat{Y} \right) = \frac{1}{ U \cdot I } \sum_{(u,i): O_{u,i} = 1} \frac{ \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right)} {P_{u,i}}
\end{aligned}
summationが$O_{u,i} = 1$で条件付けられたデータに対するものであることから, この$\hat{R}_{IPS} \left( \hat{Y} \right)$は観測可能なデータから推定可能な統計量です. 少し天下り的に与えてしまった$\hat{R}_{IPS} \left( \hat{Y} \right)$ですが, その期待値が真の評価値$R \left( \hat{Y} \right)$に一致することを次のように示すことができます.
\begin{aligned}
\mathbb{E}_O \left[ \hat{R}_{IPS} \left( \hat{Y} \right) \right] & = \mathbb{E}_O \left[ \frac{1}{ U \cdot I } \sum_{(u,i): O_{u,i} = 1} \frac{ \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right)} {P_{u,i}} \right] \\
& = \mathbb{E}_O \left[ \frac{1}{ U \cdot I } \sum_{u,i} O_{u,i} \cdot \frac{ \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right)} {P_{u,i}} \right] \\
& = \frac{1}{ U \cdot I } \sum_{u,i} \frac{\mathbb{E}_{O_{u,i}} \left[ O_{u,i} \right]} {P_{u,i}} \cdot \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right) \\
& = \frac{1}{ U \cdot I } \sum_{u,i} \delta \left( Y_{u,i}, \hat{Y}_{u, i} \right) \\
& = R \left( \hat{Y} \right)
\end{aligned}
よってBiasの観点で議論すると, Naive推定量$\hat{R}_{Naive}$ではなくてIPS推定量を使って推薦システムの評価を行うべきであると言えます.
(補足)IPS推定量の解釈
$\hat{R}_{IPS} \left( \hat{Y} \right)$は観測されたユーザーとアイテムのペアについての損失$\delta$を, その観測確率$P_{u,i}$の逆数で重み付けしています. つまり, 観測されにくかったデータにより大きな重み を与えています. この重み付けにより観測確率が小さいが観測されたデータから実際に観測されなかったデータも考慮に入れた評価をしようとしているのがIPS推定量のお気持ちとして読み取れます.
簡易実験
ここまでは簡単な映画推薦の例や理論事実を用いて, Naive推定量がBiasを持つこととIPS推定量はBiasを持たないためより望ましい評価方法であることを主張してきました. しかし本当にそうなのか腑に落ちない人もいるかもしれないので人工データを用いた実験でもこれらの事実を示していきます.
実験に用いたノートブックはこちらにあります.
人工データ
今回の実験では簡単に推薦システムを模した人工データを用います.
まず, 各ユーザーとアイテムに対応する20次元のベクトルを独立にサンプリングします. $\lambda$は適当に0.5としました.
\begin{aligned}
\theta_u \sim \mathcal{N} \left( 0, \lambda {\bf I} \right), \; \beta_i \sim \mathcal{N} \left( 0, \lambda {\bf I} \right)
\end{aligned}
次にユーザーバイアス$b_u$とアイテムバイアス$b_i$を独立にサンプリングします. こちらも$\lambda$は0.5に設定しました.
\begin{aligned}
b_u \sim \mathcal{N} \left( 0, \lambda \right), \; b_i \sim \mathcal{N} \left( 0, \lambda \right)
\end{aligned}
これらのサンプリングされたベクトルやスカラー値を用いてRatingを次のように生成したあとで, 整数値に直し, Ratingの最小値が1, 最大値が5になるような処理を加えました. 末尾のrating_biasは, ratingの全体平均を調整するために入れています. 今回の実験では3に設定しています.
\begin{aligned}
Y_{u,i} = \theta_u^{\top} \beta_i + b_u + b_i + rating\_bias
\end{aligned}
コードで書くとこのような感じになります.
# theta, beta, user_bias, item_biasからratingを生成.
preference = theta @ beta.T + user_bias + item_bias.T + rating_bias
rate = np.clip(np.round(preference), a_min=1., a_max=5.)
最後に傾向スコアを次のように生成します. $\sigma (\cdot)$はシグモイド関数です. このように傾向スコアを生成することで高いRatingを有するユーザーとアイテムのペアの観測確率が高いと言う現実に起こっていそうなBiasを意図的に起こしています. 末尾のpropensity_biasは, 観測されるユーザーとアイテムのRating行列のsparsityを調整するためのパラメータで, 今回は-5に設定しました.
\begin{aligned}
\mathbb{E} \left[O_{u,i} \right] = \sigma \left( \theta_u^{\top} \beta_i + b_u + b_i + propensity\_bias \right)
\end{aligned}
# theta, beta, user_bias, item_biasからpropensity scoreを生成.
propensity = np.clip(sigmoid(theta @ beta.T + user_bias + item_bias.T + rating_bias + propensity_bias), a_min=.0005, a_max=.20,)
上記のような過程で生成されたRatingの分布は次の通りです.
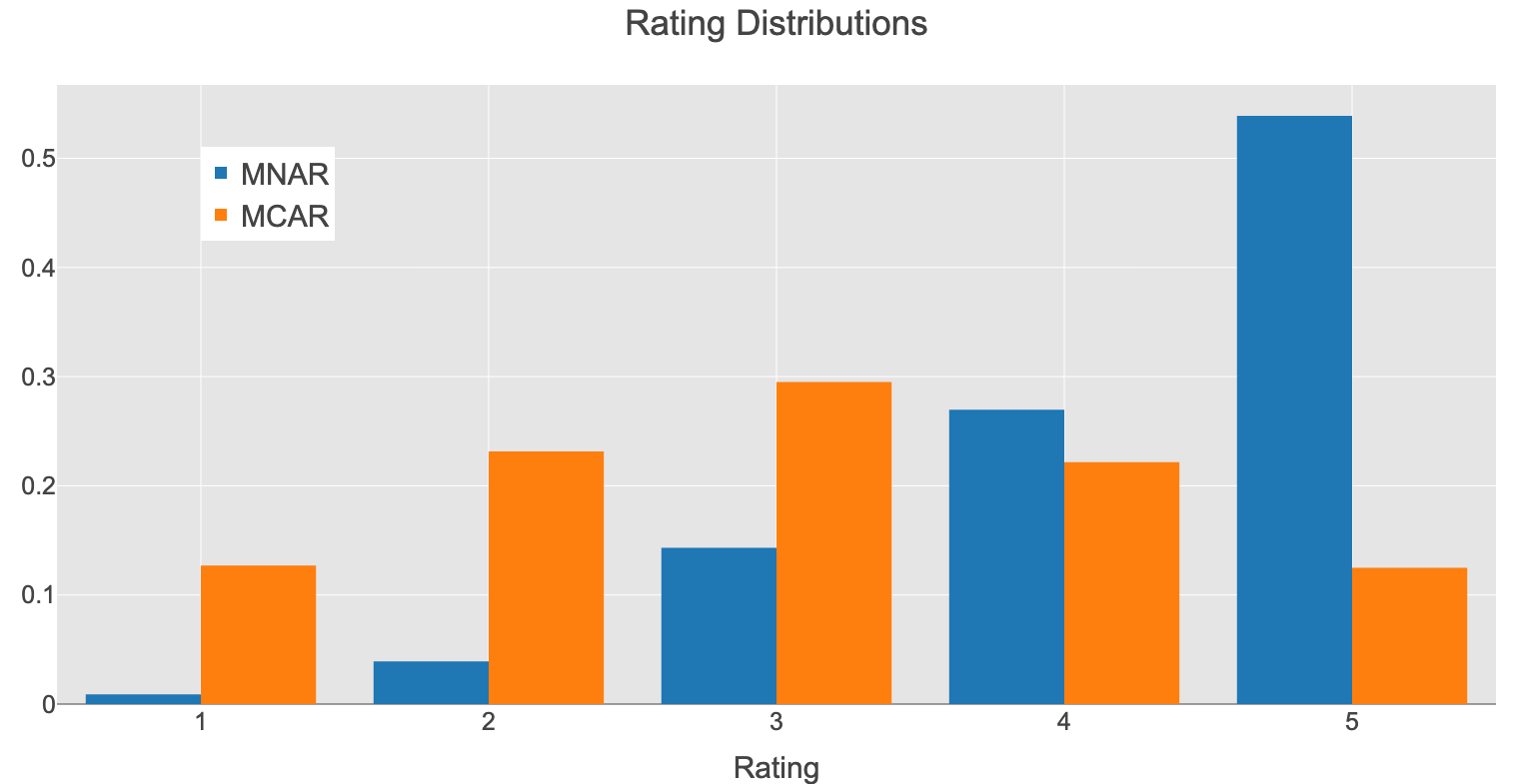
MNAR(Missing Not At Random)は観測されたデータのRating分布でMCAR(Missing Completely At Random)は真の母集団のRating分布です. この二つの分布が大きく異なっていることが一目瞭然だと思います. また, 傾向スコアの分布は次のようになりました. データごとに傾向スコアの値が大きく異なっている様子が見て取れます.
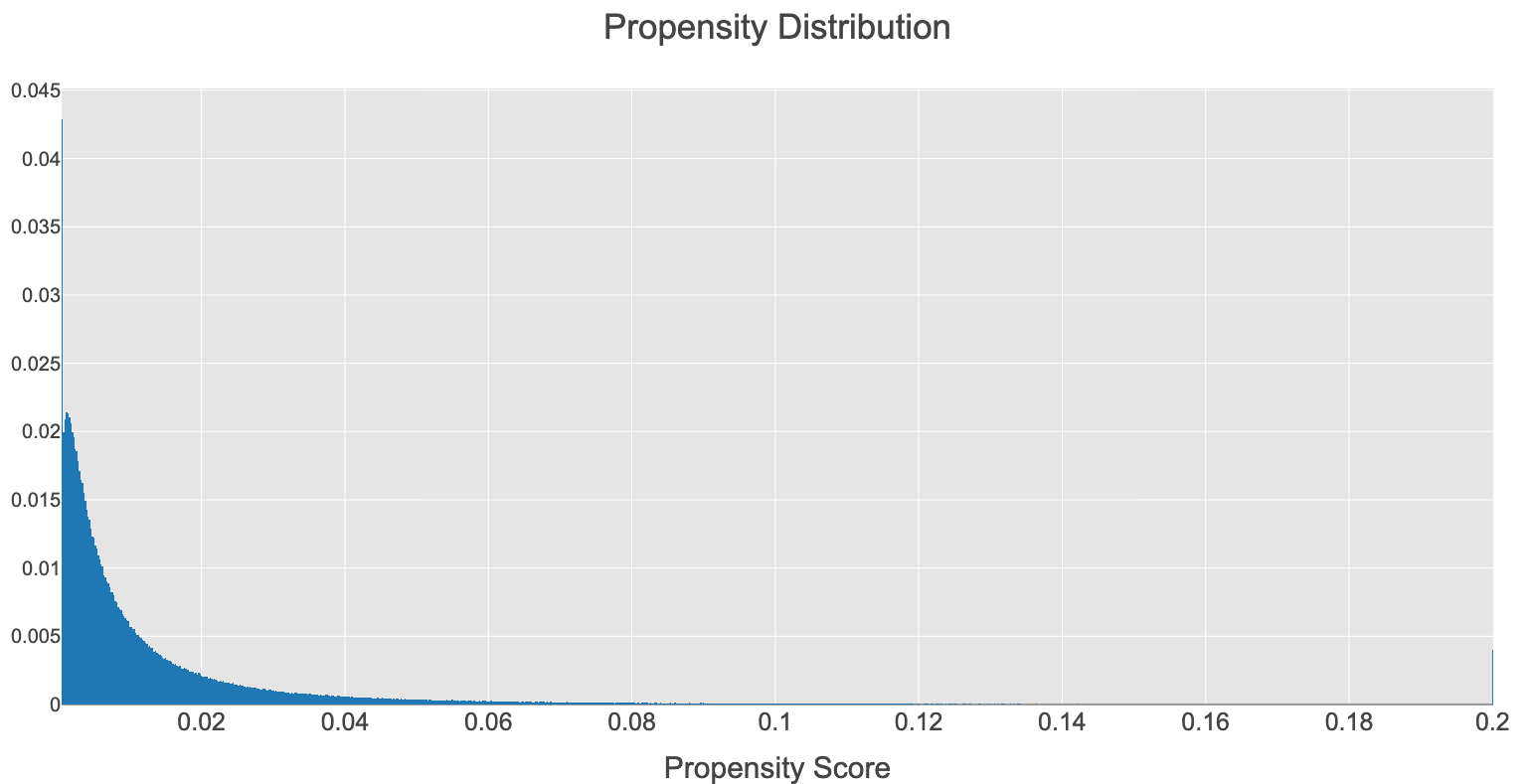
Ratingの予測集合
今回は[1]の実験に倣い, 次の5つの方法で予測値集合$\hat{Y}$を作って, それらの性能を観測データから推定することとします.
- Rec_Ones
- $Y_{u,i} \leqq 4$のユーザーとアイテムのペアについては, $\hat{Y}_{u,i} = Y_{u,i}$. $Y_{u,i} = 5$のペアについては, 1/2の確率で$\hat{Y}_{u,i} = 5$か$\hat{Y}_{u,i} = 1$.
- Rec_Fours
- $Y_{u,i} \leqq 4$のペアについては, $\hat{Y}_{u,i} = Y_{u,i}$. $Y_{u,i} = 5$のペアについては, 1/2の確率で$\hat{Y}_{u,i} = 5$か$\hat{Y}_{u,i} = 4$.
- Rotate
- $Y_{u,i} \leqq 2$のペアについては, $\hat{Y}_{u,i} = Y_{u,i} - 1$. また, $Y_{u,i} = 5$のペアについては, $\hat{Y}_{u,i} = 1$.
- Skewed
- 予測値$\hat{Y}_{u,i}$を正規分布$\mathcal{N} \left( Y_{u,i} , \frac{6 - Y_{u,i}}{2} \right)$からサンプリングした後で$[0, 6]$の区間にclipping.
- Coarsened
- $Y_{u,i} \leqq 3$のペアについては, $\hat{Y}_{u,i} = 3$. それ以外のペアについては, $\hat{Y}_{u,i}=4$.
Naive推定量とIPS推定量の比較
傾向スコアに基づいて観測されたデータから, 5つのRating予測集合のRMSEをNaive推定量とIPS推定量を使って推定し, それらの推定量とGroud Truthの値を比較しました. 結果は次の通りです.

IPS推定量の方がNaive推定量よりもGround Truthに近い推定値を返していることがわかります. また, Ground Truthに対する各推定量の相対誤差は次の通りです.
| Rec_Ones | Rec_Fours | Rotate | Skewed | Coarsened | |
|---|---|---|---|---|---|
| Naive | 1.0806 | 1.0793 | 0.2859 | 0.3457 | 0.1539 |
| IPS | 0.0027 | 0.0031 | 0.0007 | 0.0011 | 0.00002 |
IPS推定量の方が小さい誤差で性能評価ができていることが定量的にも明らかです. また, 盲目にNaive推定量を用いると真の評価値から大きく外れた性能評価になってしまう危険性があることが示されました.
最後に
本記事では, 簡単な例から入り理論事実と簡易実験により推薦システムの性能をNaive推定量で評価するとBiasが生じることと傾向スコアを用いたIPS推定量によりそのBiasを除去できることを示してきました. 今回は評価指標の構築に関する話題でしたが, 同様の問題は学習時にも発生します. 次回は, 学習アルゴリズムの損失関数設計に関する話題について書くつもりです.
参考
[1] Tobias Schnabel, Adith Swaminathan, Ashudeep Singh, Navin Chandak, and Thorsten Joachims. 2016. Recommendations as Treatments: Debiasing Learning and Evaluation. In International Conference on Machine Learning. 1670–1679.
[2] shota yasui. bandit with causality-公開版 (https://www.slideshare.net/shotayasui).