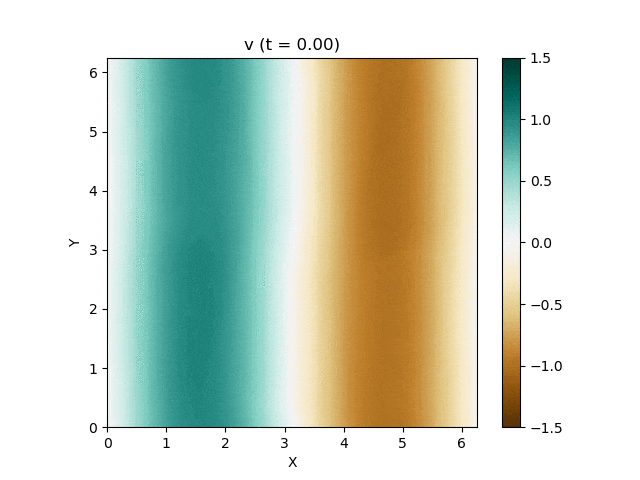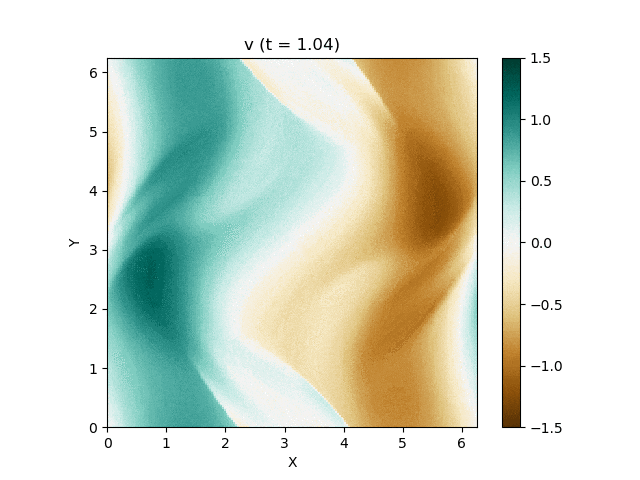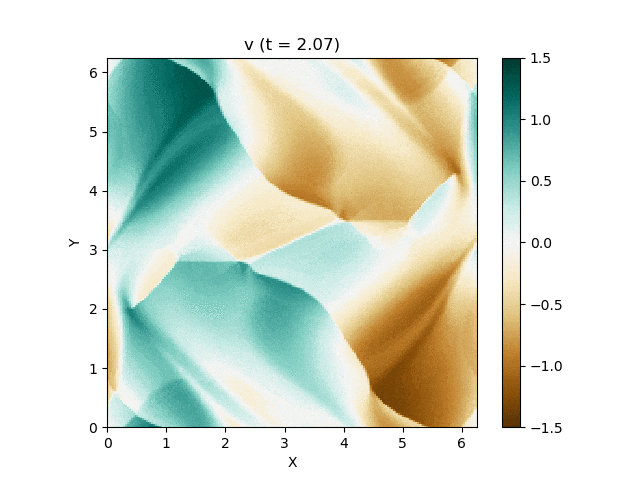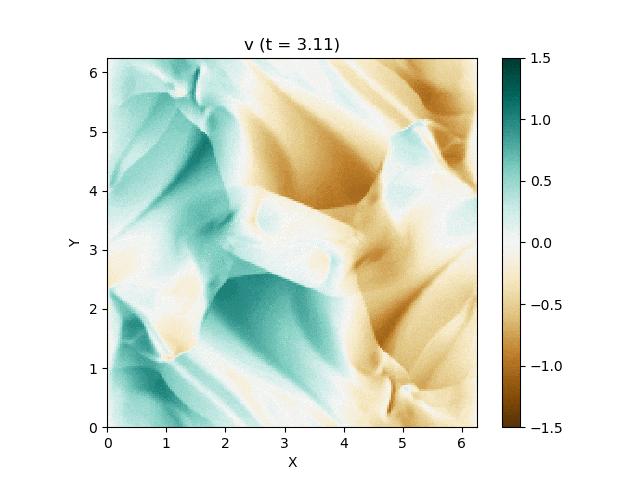磁気流体とは
プラズマや液体金属のような電気伝導性の高い流体を扱う流体力学を磁気流体力学 (Magnetohydrodynamics) といいます。英語から略してよくMHDと呼ばれます。
この磁気流体の方程式系は保存形で書くと以下のようになります。
\frac{\partial\mathbf{U}}{\partial t} + \frac{\partial\mathbf{F}}{\partial x} + \frac{\partial\mathbf{G}}{\partial y} + \frac{\partial\mathbf{H}}{\partial z}= \mathbf{0}
\mathbf{U} = \begin{bmatrix}
\rho \\
\rho u \\
\rho v \\
\rho w \\
B_x \\
B_y \\
B_z \\
e
\end{bmatrix},\
\mathbf{F} = \begin{bmatrix}
\rho u \\
\rho u^2+p_T-B_x^2 \\
\rho uv-B_xB_y \\
\rho uw-B_xB_z \\
0 \\
B_yu-B_xv \\
B_zu-B_xw \\
\left(e+p_T\right)u-B_x\left(\mathbf{v}\cdot\mathbf{B}\right)
\end{bmatrix},\
\mathbf{G} = \begin{bmatrix}
\rho v \\
\rho vu-B_yB_x \\
\rho v^2+p_T-B_y^2 \\
\rho vw-B_yB_z \\
B_xv-B_yu \\
0 \\
B_zv-B_yw \\
\left(e+p_T\right)v-B_y\left(\mathbf{v}\cdot\mathbf{B}\right)
\end{bmatrix},\
\mathbf{H} = \begin{bmatrix}
\rho w \\
\rho wu-B_zB_x \\
\rho wv-B_zB_y \\
\rho w^2+p_T-B_z^2 \\
B_xw-B_zu \\
B_yw-B_zv \\
0 \\
\left(e+p_T\right)w-B_z\left(\mathbf{v}\cdot\mathbf{B}\right)
\end{bmatrix}
p = \left(\gamma-1\right)\left(e-\frac{1}{2}\rho|\mathbf{v}|^2-\frac{1}{2}|\mathbf{B}|^2\right),\ p_T = p+\frac{1}{2}|\mathbf{B}|^2
ここで $\rho, p$ は密度・圧力で、$u, v, w$ はそれぞれ $x, y, z$ 方向の速度、$B_x, B_y, B_z$ はそれぞれ $x, y, z$ 方向の磁場、さらに $e$ はエネルギー密度を表しています。$\gamma$ は比熱比です。またここでは $\mu_0, 4\pi$ 等の磁場に関する係数が消える単位系を採用しています。
通常の流体と比べてみると、新たに磁場が変数として加わっていることがわかりますね。
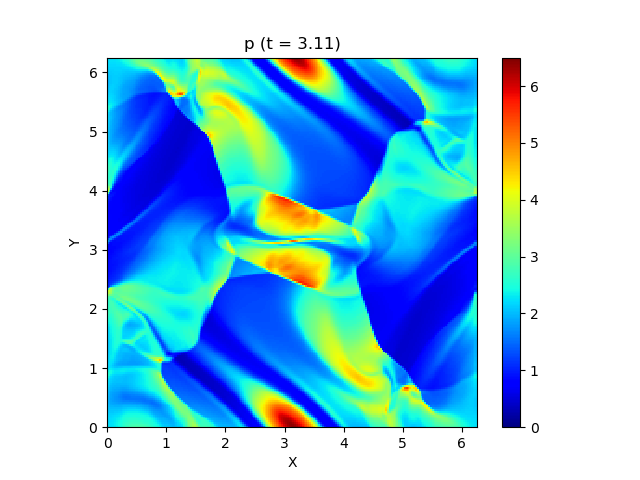
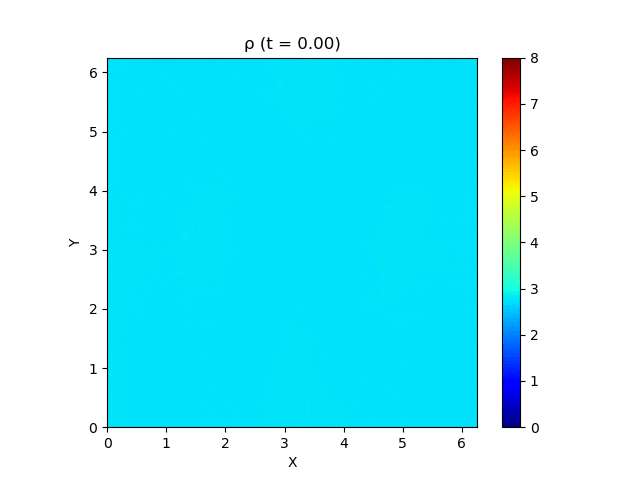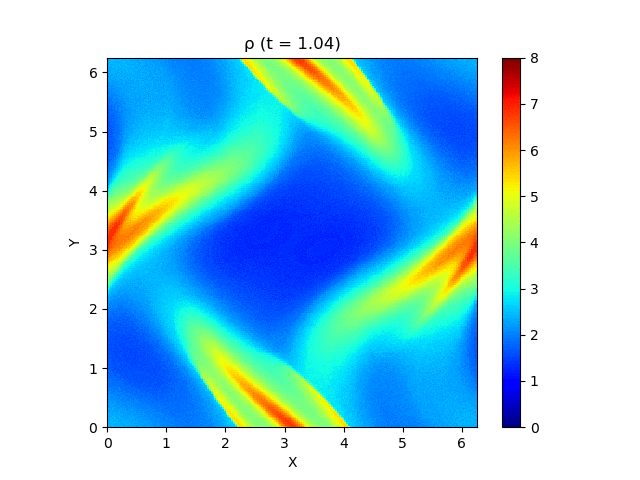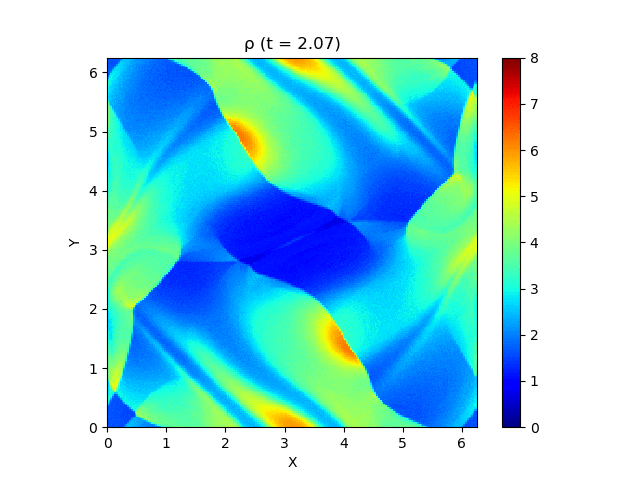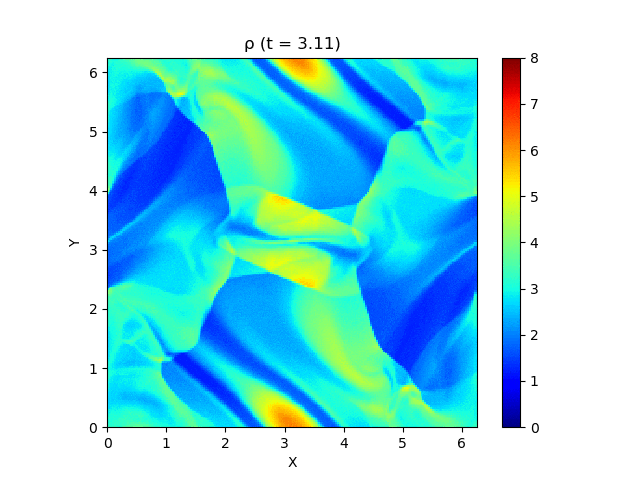
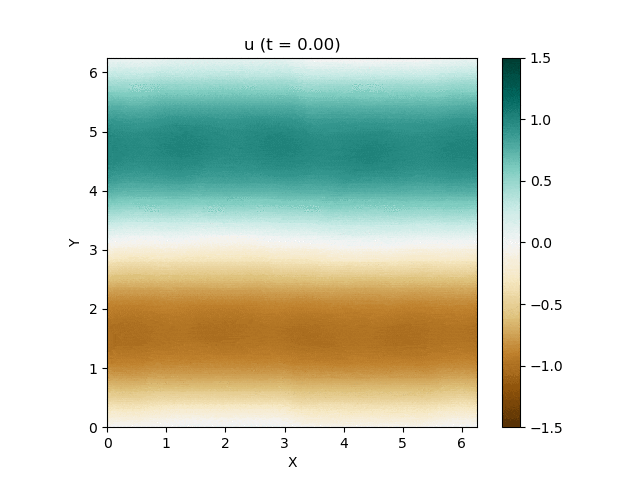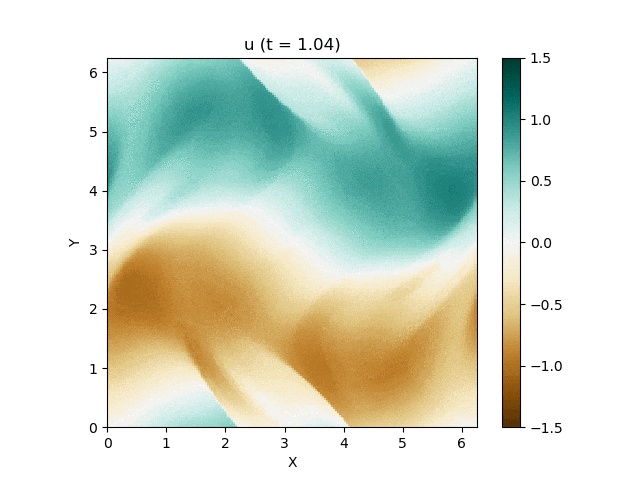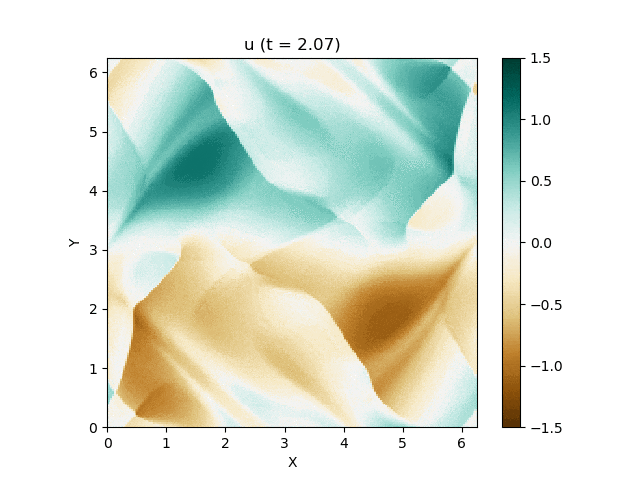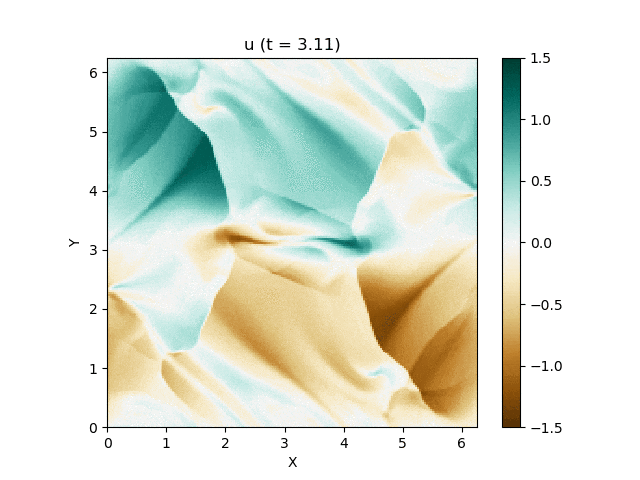
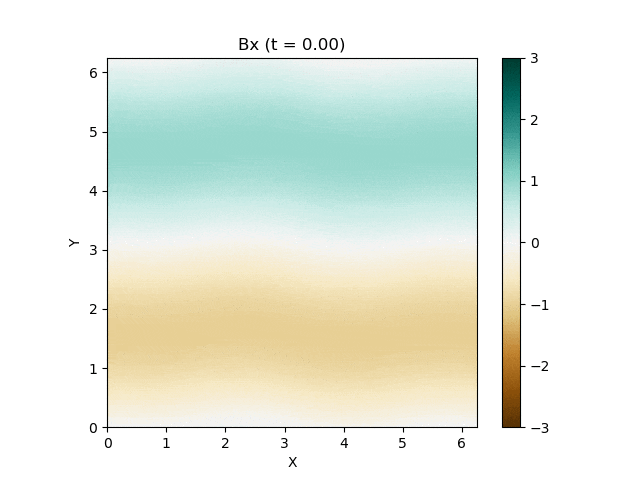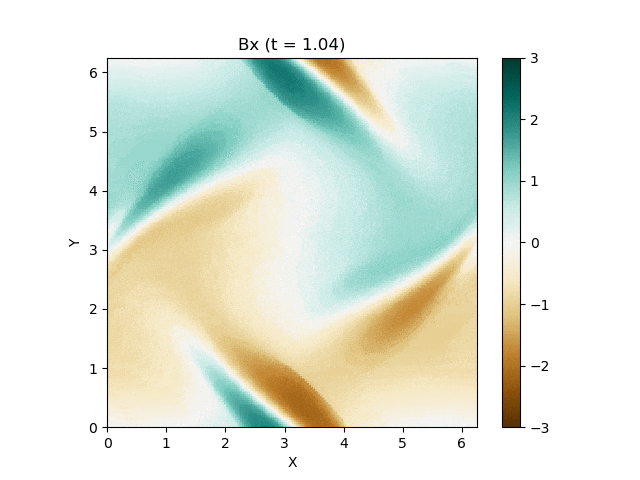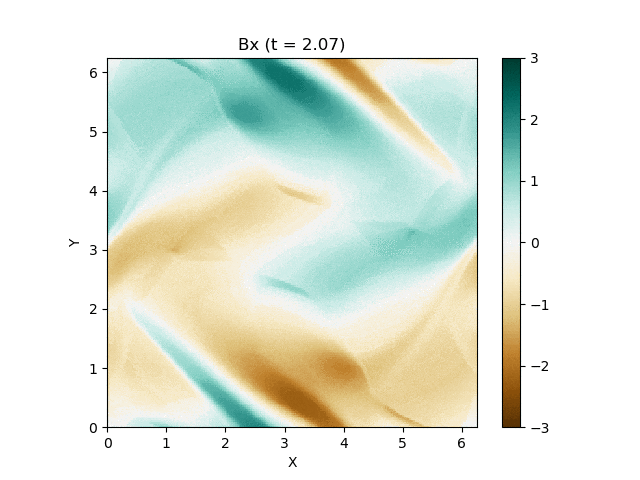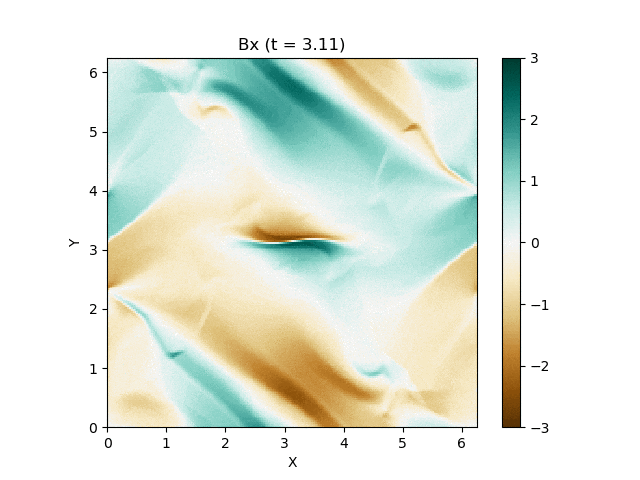
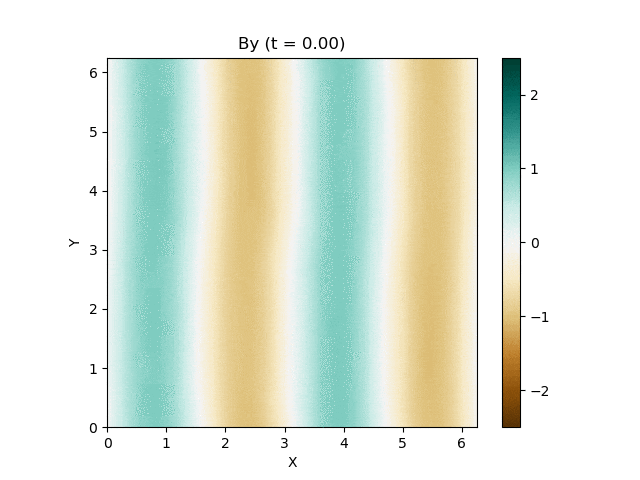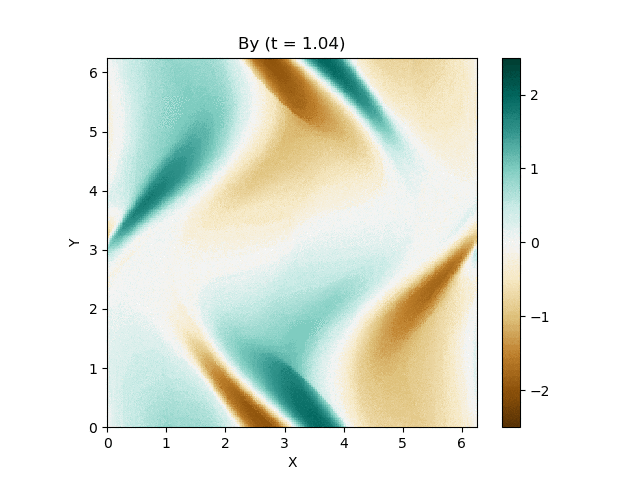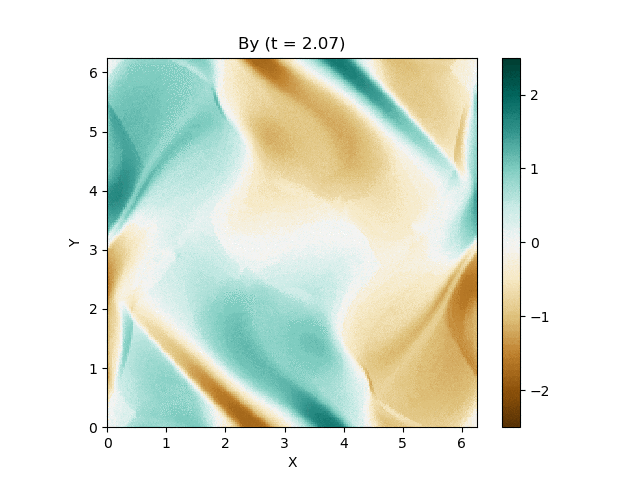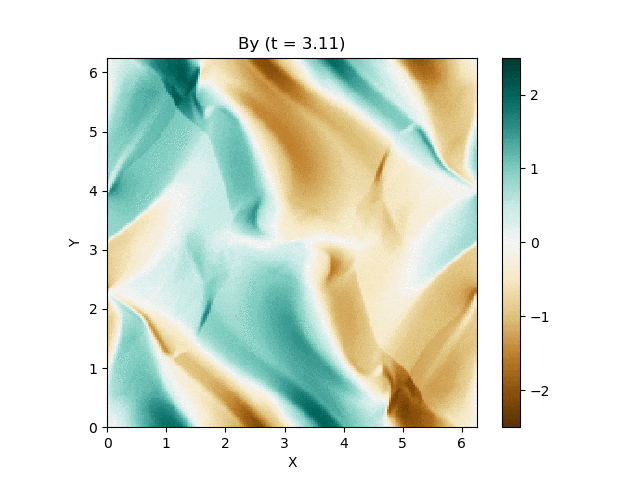
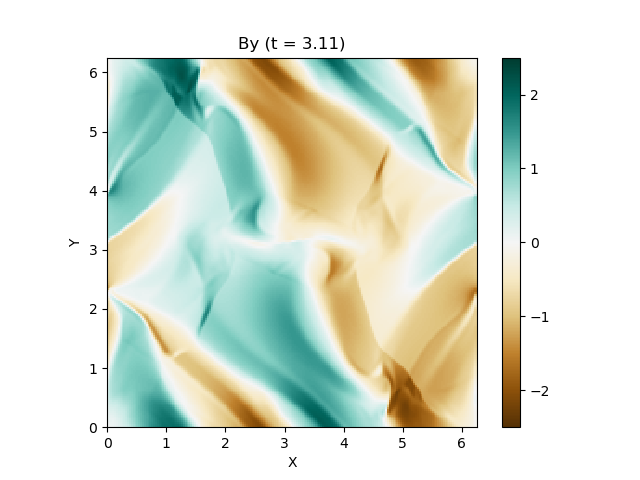
さて、この磁気流体の有名な問題にOrszag-Tang渦問題 (Orszag and Tang, 1979) というものがあります (Google画像検索) 。渦が衝撃波を形成しながら複雑に絡み合った模様が形成され、しかも数値的に発生する磁場発散を適切に除去できないと計算が破綻しやすいことが知られており、磁気流体計算の標準的なテスト問題としてよく用いられています。
具体的な設定は以下の通りです。
\rho = \gamma^2,\ p = \gamma
u = -\sin y,\ v = \sin x,\ w = 0
B_x = -\sin y,\ B_y = \sin 2x,\ B_z = 0
\gamma = 5/3,\ 0\le x \le 2\pi,\ 0\le y \le 2\pi
境界条件は $x, y$ 各方向に周期境界条件を課します。
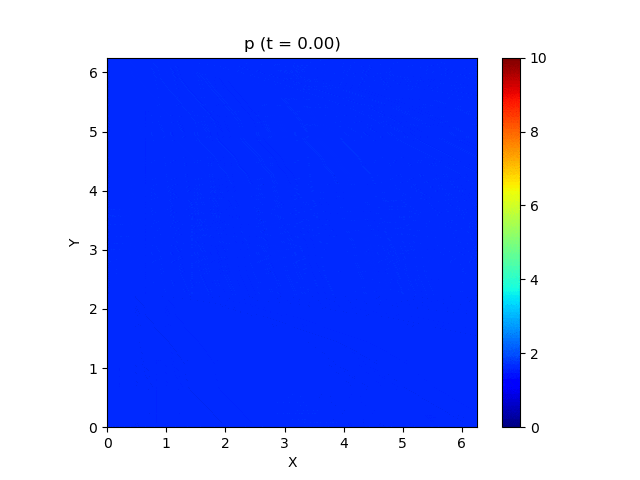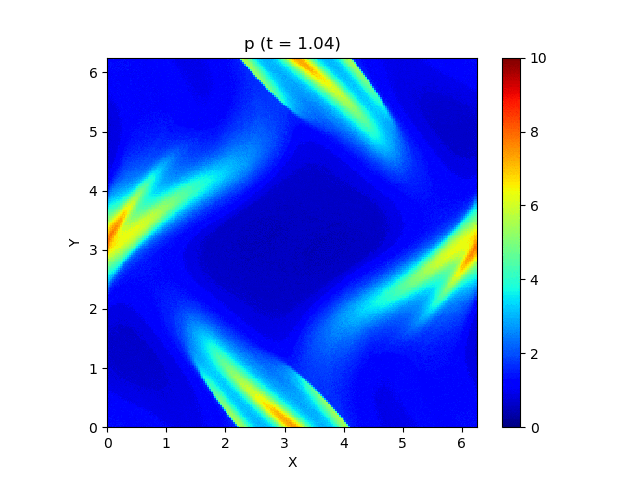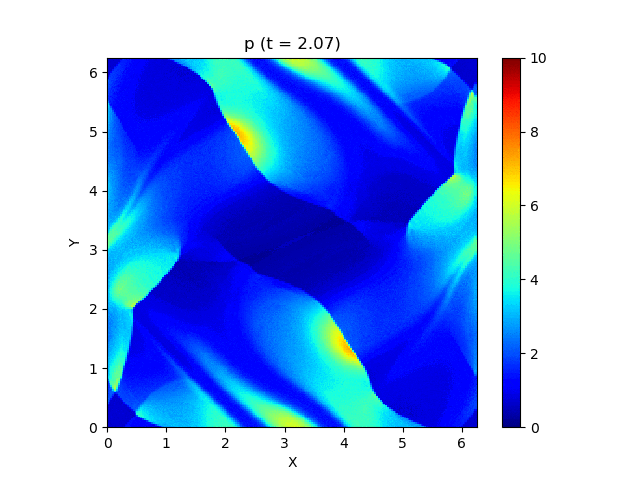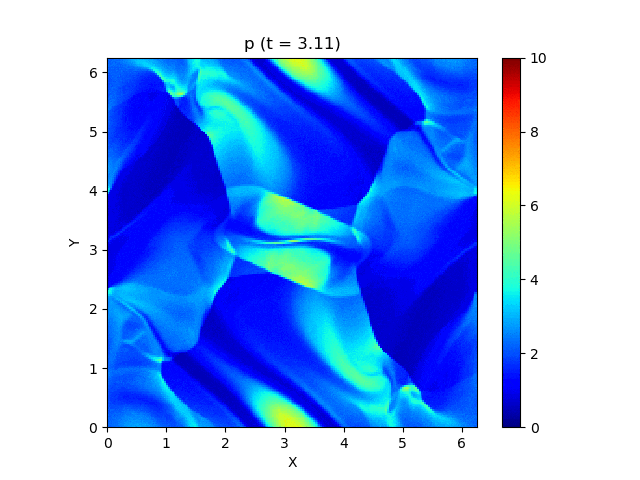
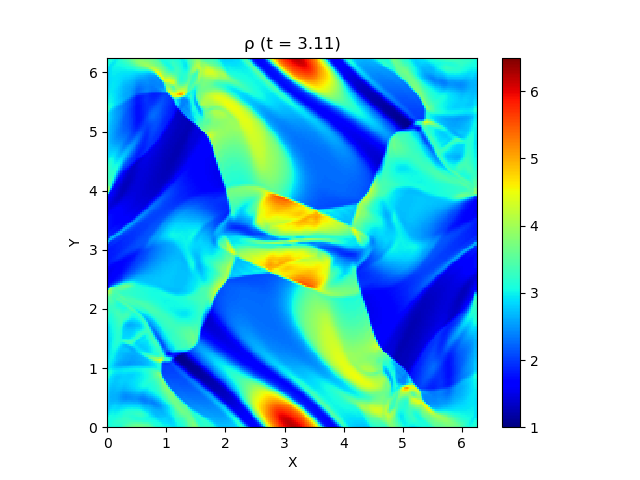
今回はこれを解くのが目標です。最終的にはこんな図が出来上がります。
HLLD近似リーマン解法
ここで一旦簡単のために1次元とします。このとき方程式系は以下のように書けます。
\frac{\partial\mathbf{U}}{\partial t} + \frac{\partial\mathbf{F}}{\partial x} = \mathbf{0}
\mathbf{U} = \begin{bmatrix}
\rho \\
\rho u \\
\rho v \\
\rho w \\
B_y \\
B_z \\
e
\end{bmatrix},\
\mathbf{F} = \begin{bmatrix}
\rho u \\
\rho u^2+p_T-B_x^2 \\
\rho uv-B_xB_y \\
\rho uw-B_xB_z \\
B_yu-B_xv \\
B_zu-B_xw \\
\left(e+p_T\right)u-B_x\left(\mathbf{v}\cdot\mathbf{B}\right)
\end{bmatrix}
1次元の場合マクスウェル方程式の
\nabla\cdot\mathbf{B} = 0
から $B_x$ は時間・空間的に常に一定となるので、$B_x$ は方程式の独立変数から外してあります。
さて、上の $\mathbf{F}$ のヤコビアンの固有値を求めることで、この磁気流体には7個の特性速度
\lambda_1 = u-c_{fx}, \lambda_2 = u-c_{ax}, \lambda_3 = u-c_{sx}, \lambda_4 = u, \lambda_5 = u+c_{sx}, \lambda_6 = u+c_{ax},\lambda_7 = u+c_{fx}
があることがわかります (導出はめちゃくちゃ面倒なので省略します)。ここで
a = \sqrt{\frac{\gamma p}{\rho}},\ c_{a} = \frac{|\mathbf{B}|}{\sqrt{\rho}}
c_{ax} = \frac{|B_x|}{\sqrt{\rho}},\ c_{fx,sx} = \left[\frac{a^2+c_a^2\pm\sqrt{\left(a^2+c_a^2\right)^2-4a^2c_{ax}^2}}{2}\right]^{1/2}
で、 $\lambda_2, \lambda_6$ はAlfvén波、$\lambda_1, \lambda_7$ は速進磁気音波 (fast magnetosonic wave)、$\lambda_3, \lambda_5$ は遅進磁気音波 (slow magnetosonic wave)、そして $\lambda_4$ はエントロピー波を表しています。
通常の流体が前後の音波とエントロピー波の合計3種類だったことを考えると、随分波の種類が増えています。うーんこれは大変そう。
何しろ多くの場合無視される遅進磁気音波抜きにしても5個です。これら多種多様な波を的確に捉えて計算するのは、通常の流体と比べてもかなり難易度が高くなります。
そんななか、HLLD近似リーマン解法 (Miyoshi and Kusano, 2005) は精度・計算効率・ロバスト性いずれも優れた解法として広く用いられており、今回はこれを採用したいと思います。
ここで以下のような原点を境に不連続に配置された初期値問題を考えます。
\mathbf{U} = \begin{cases}
\mathbf{U}_L & (x < 0) \\
\mathbf{U}_R & (x > 0)
\end{cases}
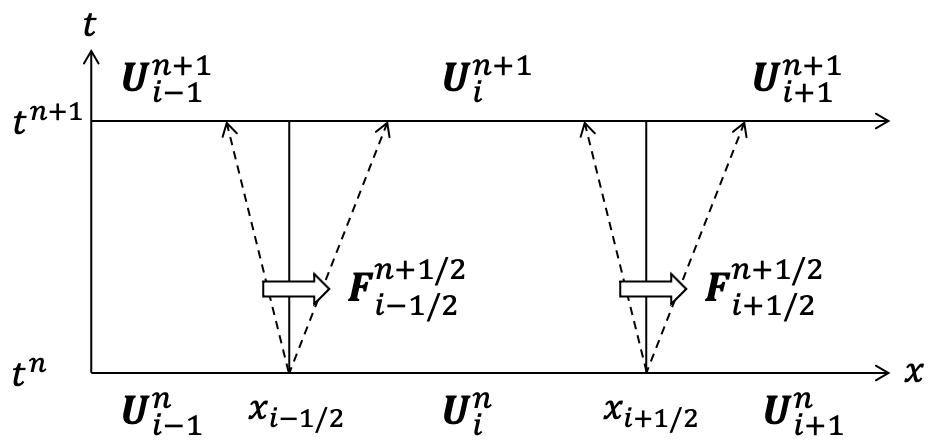
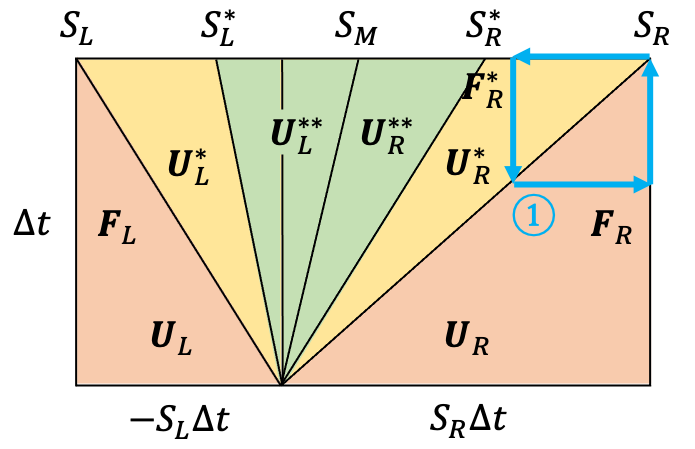
これをリーマン問題といい、HLLD法をはじめとする近似リーマン解法系のスキームでは、各セル内では $\mathbf{U}$ が一様になっていると近似して、各セルの境界毎のリーマン問題に帰着させます (下図)。
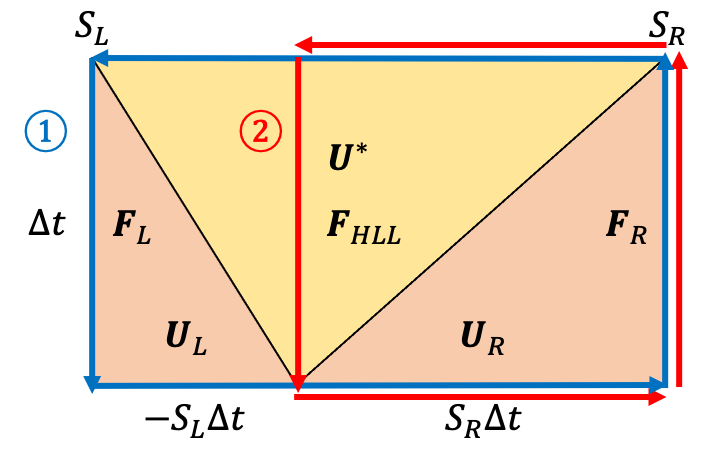
そこでHLLD法の説明に入る前に、より単純なHLL法を説明します (後でこの結果を使います)。リーマン問題の解は中心からさまざまな波が広がってゆく、という形になりますが、HLL法では左向きの波 $S_L$ と右向きの波 $S_R$ の2種類のみを考えます。さらに2つの波に囲まれた領域 (リーマンファン) 内で $\mathbf{U}$ は一定と近似します。
この2つの波には左右に一番速い速進磁気音波を選び、その速さは
S_L = \mathrm{min}\left(u_L-{c_{fx}}_L, u_R-{c_{fx}}_R\right), S_R = \mathrm{max}\left(u_L+{c_{fx}}_L, u_R+{c_{fx}}_R\right)
または
S_L = \mathrm{min}\left(u_L, u_R\right)-\mathrm{max}\left({c_{fx}}_L, {c_{fx}}_R\right), S_R = \mathrm{max}\left(u_L, u_R\right)+\mathrm{max}\left({c_{fx}}_L, {c_{fx}}_R\right)
などと求めます。
方程式を $x-t$ 平面内でグリーンの定理を使って積分すると
\iint_S\left(\frac{\partial\mathbf{U}}{\partial t}+\frac{\partial\mathbf{F}}{\partial x}\right)dxdt = \oint_c\left(-\mathbf{U}dx+\mathbf{F}dt\right) = \mathbf{0}
となるので、下図積分路①について、
-S_R\mathbf{U}_R+S_L\mathbf{U}_L+\mathbf{F}_R-\mathbf{F}_L+\left(S_R-S_L\right)\mathbf
{U}^* = \mathbf{0}
積分路②について、
-S_R\mathbf{U}_R+\mathbf{F}_R-\mathbf{F}_{HLL}+S_R\mathbf
{U}^* = \mathbf{0}
したがって、中間状態の $\mathbf{U}^*$ と $\mathbf{F}_{HLL}$ は、
\begin{aligned}
\mathbf{U}^* &= \frac{S_R\mathbf{U}_R-S_L\mathbf{U}_L-\mathbf{F}_R+\mathbf{F}_L}{S_R-S_L} \\
\mathbf{F}_{HLL} &= \mathbf{F}_R+S_R\left(\mathbf{U}^*-\mathbf{U}_R\right) \\
&= \frac{S_R\mathbf{F}_L-S_L\mathbf{F}_R+S_R S_L\left(\mathbf{U}_R-\mathbf{U}_L\right)}{S_R-S_L}
\end{aligned}
と得られます。
ここでは一旦 $S_L < 0 < S_R$ の場合を考えていますが、もし $S_L > 0$ の場合には $\mathbf{F}_L$ を、$S_R < 0$ の場合には $\mathbf{F}_R$ をそれぞれセル境界でのフラックスとすればOKです。
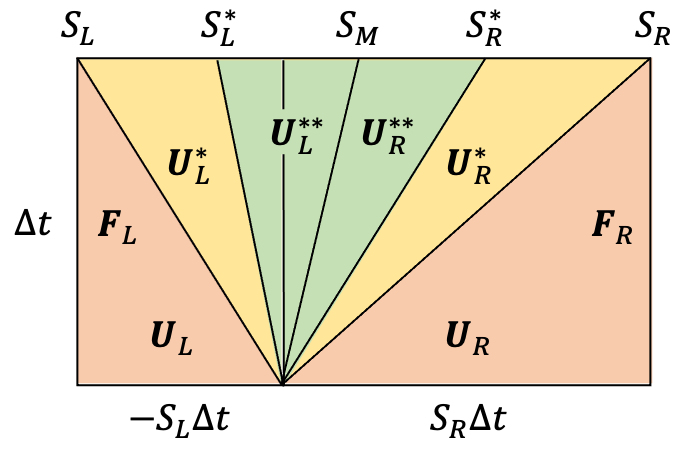
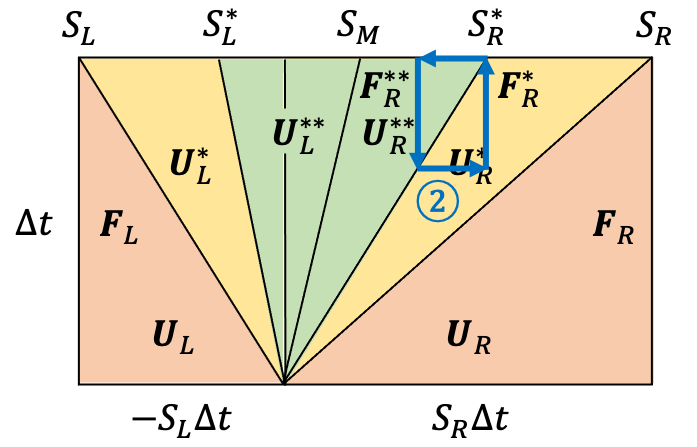
次に以上の方法を拡張してHLLD法を導出してみましょう。HLLD法ではリーマンファン内で $u$ が一定と仮定します。これによって $p_T$ も一定となり、遅進磁気音波が除外されます。なのでこの場合リーマン問題の解は、下図のように
- 速進磁気音波より速い領域 × 2
- 速進磁気音波とAlfvén波の間の領域 × 2
- Alfvén波とエントロピー波の間の領域 × 2
の6領域に分かれます。
ここから領域内の $\mathbf{U}$ を次々求めてゆきましょう。
まず前提から以下が成り立ちます。
u^*_L = u^{**}_L = u^{**}_R = u^*_R \equiv S_M
{p_T}^*_L = {p_T}^{**}_L = {p_T}^{**}_R = {p_T}^*_R \equiv {p_T}^*
$S_M$ はHLL法で得られた $\rho_{HLL}$ と $\left(\rho u\right)_{HLL}$ を使って以下のように求めます。
S_M = \frac{\left(\rho u\right)_{HLL}}{\rho_{HLL}} = \frac{\left(S_R-u_R\right)\rho_R u_R-\left(S_L-u_L\right)\rho_L u_L-{p_T}_R+{p_T}_L}{\left(S_R-u_R\right)\rho_R-\left(S_L-u_L\right)\rho_L}
速進磁気音波に対するジャンプ条件
まず速進磁気音波の前後で値がどのように変わるか見てみましょう。
そのために積分路①を下図のように半分ずつ $\mathbf{U}_R$ の領域と $\mathbf{U}^*_R$ の領域が入るようにとります。
このとき
S_R\mathbf{U}_R-\mathbf{F}\left(\mathbf{U}_R\right) = S_R\mathbf{U}^*_R-\mathbf{F}\left(\mathbf{U}^*_R\right)
で、これを具体的に成分で書くと以下のようになります。
S_R\begin{bmatrix}
\rho_R \\
\rho_R u_R \\
\rho_R v_R \\
\rho_R w_R \\
{B_y}_R \\
{B_z}_R \\
e_R
\end{bmatrix}
-
\begin{bmatrix}
\rho_R u_R \\
\rho_R u_R^2+{p_T}_R-B_x^2 \\
\rho_R u_R v_R-B_x{B_y}_R \\
\rho_R u_R w_R-B_x{B_z}_R \\
{B_y}_R u_R-B_x v_R \\
{B_z}_R u_R-B_x w_R \\
\left(e_R+{p_T}_R\right)u_R-B_x \left(\mathbf{v}_R\cdot\mathbf{B}_R\right)
\end{bmatrix}
=
S_R\begin{bmatrix}
\rho^*_R \\
\rho^*_R S_M \\
\rho^*_R v^*_R \\
\rho^*_R w^*_R \\
{B_y}^*_R \\
{B_z}^*_R \\
e^*_R
\end{bmatrix}
-
\begin{bmatrix}
\rho^*_R S_M \\
\rho^*_R S_M^2+{p_T}^*-B_x^2 \\
\rho^*_R S_M v^*_R-B_x{B_y}^*_R \\
\rho^*_R S_M w^*_R-B_x{B_z}^*_R \\
{B_y}^*_R S_M-B_x v^*_R \\
{B_z}^*_R S_M-B_x w^*_R \\
\left(e^*_R+{p_T}^*\right)S_M-B_x \left(\mathbf{v}^*_R\cdot\mathbf{B}^*_R\right)
\end{bmatrix}
左側についても同様に考えることで、ここから $\mathbf{U}^*_\alpha$ が以下のように求められます。$\alpha$ はLまたはRという意味です。
\begin{aligned}
\rho^*_\alpha &= \rho_\alpha\frac{S_\alpha-u_\alpha}{S_\alpha-S_M} \\
v^*_\alpha &= v_\alpha-B_x {B_y}_\alpha\frac{S_M-u_\alpha}{\rho_\alpha\left(S_\alpha-u_\alpha\right)\left(S_\alpha-S_M\right)-B_x^2} \\
w^*_\alpha &= w_\alpha-B_x {B_z}_\alpha\frac{S_M-u_\alpha}{\rho_\alpha\left(S_\alpha-u_\alpha\right)\left(S_\alpha-S_M\right)-B_x^2} \\
{B_y}^*_\alpha &= {B_y}_\alpha\frac{\rho_\alpha\left(S_\alpha-u_\alpha\right)^2-B_x^2}{\rho_\alpha\left(S_\alpha-u_\alpha\right)\left(S_\alpha-S_M\right)-B_x^2} \\
{B_z}^*_\alpha &= {B_z}_\alpha\frac{\rho_\alpha\left(S-u_\alpha\right)^2-B_x^2}{\rho_\alpha\left(S_\alpha-u_\alpha\right)\left(S_\alpha-S_M\right)-B_x^2}
\end{aligned}
\begin{aligned}
p_T^* &= {p_T}_L+\rho_L\left(S_L-u_L\right)\left(S_M-u_L\right) \\
&= {p_T}_R+\rho_R\left(S_R-u_R\right)\left(S_M-u_R\right) \\
&= \frac{\left(S_R-u_R\right)\rho_R{p_T}_L-\left(S_L-u_L\right)\rho_L{p_T}_R+\rho_L\rho_R\left(S_R-u_R\right)\left(S_L-u_L\right)\left(u_R-u_L\right)}{\left(S_R-u_R\right)\rho_R-\left(S_L-u_L\right)\rho_L}
\end{aligned}
e^*_\alpha = \frac{\left(S_\alpha-u_\alpha\right)e_\alpha-{p_T}_\alpha u_\alpha+p_T^*S_M+B_x\left(\mathbf{v}_\alpha\cdot\mathbf{B}_\alpha-\mathbf{v}^*_\alpha\cdot\mathbf{B}^*_\alpha\right)}{S_\alpha-S_M}
Alfvén波に対するジャンプ条件
次にAlfvén波の前後の変化を見るために、積分路②を下図のように半分ずつ $\mathbf{U}^*_R$ の領域と $\mathbf{U}^{**}_R$ の領域が入るようにとります。
ここで $S^{*}_L$ と $S^{*}_R$ は
S^*_L = S_M-\frac{|B_x|}{\sqrt{\rho^*_L}},\ S^*_R = S_M+\frac{|B_x|}{\sqrt{\rho^*_R}}
ととります。積分路①の場合と同様にして、
S^*_R\mathbf{U}^*_R-\mathbf{F}\left(\mathbf{U}^*_R\right) = S^*_R\mathbf{U}^{**}_R-\mathbf{F}\left(\mathbf{U}^{**}_R\right)
S^*_R\begin{bmatrix}
\rho^*_R \\
\rho^*_R S_M \\
\rho^*_R v^*_R \\
\rho^*_R w^*_R \\
{B_y}^*_R \\
{B_z}^*_R \\
e^*_R
\end{bmatrix}
-
\begin{bmatrix}
\rho^*_R S_M \\
\rho^*_R S_M^2+{p_T}^*-B_x^2 \\
\rho^*_R S_M v^*_R-B_x{B_y}^*_R \\
\rho^*_R S_M w^*_R-B_x{B_z}^*_R \\
{B_y}^*_R S_M-B_x v^*_R \\
{B_z}^*_R S_M-B_x w^*_R \\
\left(e^*_R+{p_T}^*\right)S_M-B_x \left(\mathbf{v}^*_R\cdot\mathbf{B}^*_R\right)
\end{bmatrix}
=
S^*_R\begin{bmatrix}
\rho^{**}_R \\
\rho^{**}_R S_M \\
\rho^{**}_R v^{**}_R \\
\rho^{**}_R w^{**}_R \\
{B_y}^{**}_R \\
{B_z}^{**}_R \\
e^{**}_R
\end{bmatrix}
-
\begin{bmatrix}
\rho^{**}_R S_M \\
\rho^{**}_R S_M^2+{p_T}^*-B_x^2 \\
\rho^{**}_R S_M v^{**}_R-B_x{B_y}^{**}_R \\
\rho^{**}_R S_M w^{**}_R-B_x{B_z}^{**}_R \\
{B_y}^{**}_R S_M-B_x v^{**}_R \\
{B_z}^{**}_R S_M-B_x w^{**}_R \\
\left(e^{**}_R+{p_T}^*\right)S_M-B_x \left(\mathbf{v}^{**}_R\cdot\mathbf{B}^{**}_R\right)
\end{bmatrix}
となります。ここからわかるのは以下の $\rho^{**}_\alpha$ だけです。
\rho^{**}_\alpha = \rho^*_\alpha
エントロピー波に対するジャンプ条件
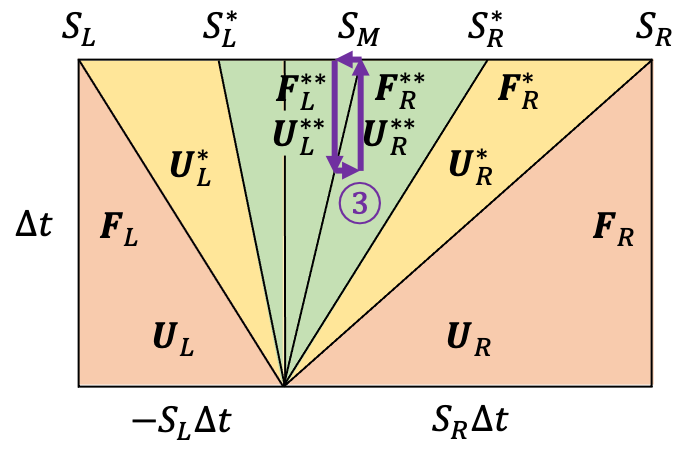
さらに下図積分路③を考えます。
S_M\mathbf{U}^{**}_L-\mathbf{F}\left(\mathbf{U}^{**}_L\right) = S_M\mathbf{U}^{**}_R-\mathbf{F}\left(\mathbf{U}^{**}_R\right)
S_M\begin{bmatrix}
\rho^*_L \\
\rho^*_L S_M \\
\rho^*_L v^{**}_L \\
\rho^*_L w^{**}_L \\
{B_y}^{**}_L \\
{B_z}^{**}_L \\
e^{**}_L
\end{bmatrix}
-
\begin{bmatrix}
\rho^*_L S_M \\
\rho^*_L S_M^2+{p_T}^*-B_x^2 \\
\rho^*_L S_M v^{**}_L-B_x{B_y}^{**}_L \\
\rho^*_L S_M w^{**}_L-B_x{B_z}^{**}_L \\
{B_y}^{**}_L S_M-B_x v^{**}_L \\
{B_z}^{**}_L S_M-B_x w^{**}_L \\
\left(e^{**}_L+{p_T}^*\right)S_M-B_x \left(\mathbf{v}^{**}_L\cdot\mathbf{B}^{**}_L\right)
\end{bmatrix}
=
S_M\begin{bmatrix}
\rho^*_R \\
\rho^*_R S_M \\
\rho^*_R v^{**}_R \\
\rho^*_R w^{**}_R \\
{B_y}^{**}_R \\
{B_z}^{**}_R \\
e^{**}_R
\end{bmatrix}
-
\begin{bmatrix}
\rho^*_R S_M \\
\rho^*_R S_M^2+{p_T}^*-B_x^2 \\
\rho^*_R S_M v^{**}_R-B_x{B_y}^{**}_R \\
\rho^*_R S_M w^{**}_R-B_x{B_z}^{**}_R \\
{B_y}^{**}_R S_M-B_x v^{**}_R \\
{B_z}^{**}_R S_M-B_x w^{**}_R \\
\left(e^{**}_R+{p_T}^*\right)S_M-B_x \left(\mathbf{v}^{**}_R\cdot\mathbf{B}^{**}_R\right)
\end{bmatrix}
ここから以下のように $v^{**}$, $w^{**}$, ${B_y}^{**}$, ${B_z}^{**}$ が左右で等しいことが示されます。
\begin{aligned}
v^{**}_L &= v^{**}_R \equiv v^{**} \\
w^{**}_L &= w^{**}_R \equiv w^{**} \\
{B_y}^{**}_L &= {B_y}^{**}_R \equiv {B_y}^{**} \\
{B_z}^{**}_L &= {B_z}^{**}_R \equiv {B_z}^{**}
\end{aligned}
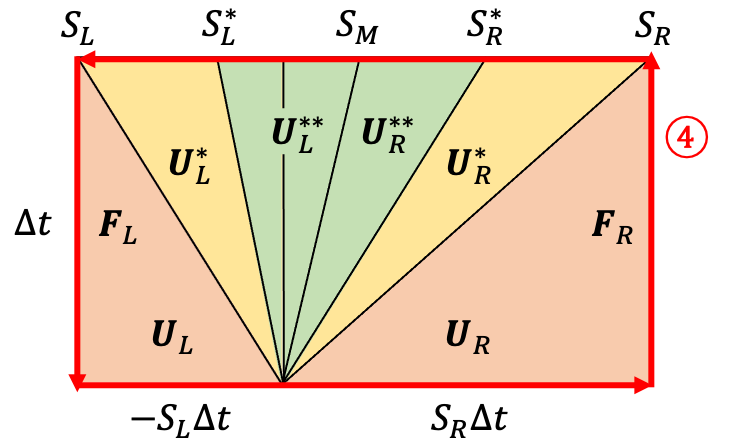
これを踏まえ、今度は下図積分路④で積分します。
\begin{aligned}
\mathbf{0} &= -S_R\mathbf{U}_R+S_L\mathbf{U}_L+\mathbf{F}_R-\mathbf{F}_L+\left(S_R-S^*_R\right)\mathbf{U}^*_R+\left(S^*_L-S_L\right)\mathbf{U}^*_L+\left(S^*_R-S_M\right)\mathbf{U}^{**}_R+\left(S_M-S^*_L\right)\mathbf{U}^{**}_L \\
&= -S^*_R\mathbf{U}^*_R+S^*_L\mathbf{U}^*_L+\mathbf{F}^*_R-\mathbf{F}^*_L+\left(S^*_R-S_M\right)\mathbf{U}^{**}_R+\left(S_M-S^*_L\right)\mathbf{U}^{**}_L \\
&= -\left(S_M+\frac{|B_x|}{\sqrt{\rho^*_R}}\right)\mathbf{U}^*_R+\left(S_M-\frac{|B_x|}{\sqrt{\rho^*_L}}\right)\mathbf{U}^*_L+\mathbf{F}^*_R-\mathbf{F}^*_L+\frac{|B_x|}{\sqrt{\rho^*_R}}\mathbf{U}^{**}_R+\frac{|B_x|}{\sqrt{\rho^*_L}}\mathbf{U}^{**}_L
\end{aligned}
ここから、
\begin{aligned}
v^{**} &= \frac{\sqrt{\rho^*_L}v^*_L+\sqrt{\rho^*_R}v^*_R+\left({B_y}^*_R-{B_y}^*_L\right)\mathrm{sign}\left(B_x\right)}{\sqrt{\rho^*_L}+\sqrt{\rho^*_R}} \\
w^{**} &= \frac{\sqrt{\rho^*_L}w^*_L+\sqrt{\rho^*_R}w^*_R+\left({B_z}^*_R-{B_z}^*_L\right)\mathrm{sign}\left(B_x\right)}{\sqrt{\rho^*_L}+\sqrt{\rho^*_R}} \\
B_y^{**} &= \frac{\sqrt{\rho^*_L}{B_y}^*_R+\sqrt{\rho^*_R}{B_y}^*_L+\sqrt{\rho^*_L\rho^*_R}\left(v^*_R-v^*_L\right)\mathrm{sign}\left(B_x\right)}{\sqrt{\rho^*_L}+\sqrt{\rho^*_R}} \\
B_z^{**} &= \frac{\sqrt{\rho^*_L}{B_z}^*_R+\sqrt{\rho^*_R}{B_z}^*_L+\sqrt{\rho^*_L\rho^*_R}\left(w^*_R-w^*_L\right)\mathrm{sign}\left(B_x\right)}{\sqrt{\rho^*_L}+\sqrt{\rho^*_R}}
\end{aligned}
最後にAlfvén波に対するジャンプ条件をもう一度使うことで、以下が得られます。
e^{**}_\alpha = e^*_\alpha\mp\sqrt{\rho^*_\alpha}\left(\mathbf{v}^*_\alpha\cdot\mathbf{B}^*_\alpha-\mathbf{v}^{**}\cdot\mathbf{B}^{**}\right)\mathrm{sign}\left(B_x\right)
複号はLのときマイナス、Rのときプラスをとります。
長くなりましたが、これで各領域の $\mathbf{U}$ がすべて求まりました。
以上をまとめますと最終的に以下の式になります。
\mathbf{F}_{HLLD} = \begin{cases}
\mathbf{F}_L & (0 < S_L) \\
\mathbf{F}_L^* & (S_L \le 0 < S_L^*) \\
\mathbf{F}_L^{**} & (S_L^* \le 0 < S_M) \\
\mathbf{F}_R^{**} & (S_M \le 0 < S_R^*) \\
\mathbf{F}_R^* & (S_R^* \le 0 < S_R) \\
\mathbf{F}_R & (S_R < 0)
\end{cases}
多次元化
多次元化を行うためには、単にHLLD法を $x,y,z$ 方向それぞれに適用すればよさそうな気がしますが、実際にはそう単純にはいかないところが磁気流体計算の難しさの一つです。
ここで問題になるのが磁場の発散です。本来ならマクスウェル方程式から磁場は常に非発散、つまり
\nabla\cdot\mathbf{B} = 0
でなければなりませんが、数値計算の場合誤差によってこれが破れることがあり、時には計算を破綻させてしまうほどの悪影響を及ぼします。これを回避する方法としては、大きく分けて
- 配置等を工夫することで磁場発散を初めから発生させない方法
- 方程式に変更を加えることで発生した磁場発散を抑制する方法
の2種類があります。前者はCT法が有名です。後者ではプロジェクション法や9 wave法が知られており、ここでは実装の比較的単純な9 wave法を紹介します。
9 wave法
Dedner et al. (2002) で提案された方法で、$\psi$ という新しい変数を導入して以下のように方程式を拡張します。
\frac{\partial\mathbf{U}}{\partial t} + \frac{\partial\mathbf{F}}{\partial x} + \frac{\partial\mathbf{G}}{\partial y} + \frac{\partial\mathbf{H}}{\partial z} = \mathbf{S}
\mathbf{U} = \begin{bmatrix}
\rho \\
\rho u \\
\rho v \\
\rho w \\
B_x \\
B_y \\
B_z \\
e \\
\psi
\end{bmatrix},\
\mathbf{F} = \begin{bmatrix}
\rho u \\
\rho u^2+p_T-B_x^2 \\
\rho uv-B_xB_y \\
\rho uw-B_xB_z \\
\psi \\
B_yu-B_xv \\
B_zu-B_xw \\
\left(e+p_T\right)u-B_x\left(\mathbf{v}\cdot\mathbf{B}\right) \\
c_h^2 B_x
\end{bmatrix},\
\mathbf{G} = \begin{bmatrix}
\rho v \\
\rho vu-B_yB_x \\
\rho v^2+p_T-B_y^2 \\
\rho vw-B_yB_z \\
B_xv-B_yu \\
\psi \\
B_zv-B_yw \\
\left(e+p_T\right)v-B_y\left(\mathbf{v}\cdot\mathbf{B}\right) \\
c_h^2 B_y
\end{bmatrix},\
\mathbf{H} = \begin{bmatrix}
\rho w \\
\rho wu-B_zB_x \\
\rho wv-B_zB_y \\
\rho w^2+p_T-B_z^2 \\
B_xw-B_zu \\
B_yw-B_zv \\
\psi \\
\left(e+p_T\right)w-B_z\left(\mathbf{v}\cdot\mathbf{B}\right) \\
c_h^2 B_z
\end{bmatrix},\
\mathbf{S} = \begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
-\frac{c_h^2}{c_p^2}\psi
\end{bmatrix}
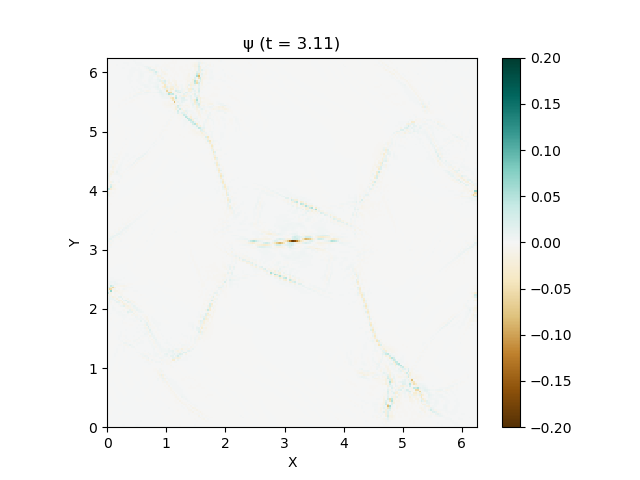
この $\psi$ は磁場発散を抑制するために人工的に導入された変数なので、何か物理的な意味があるわけではありません。
セル境界での $B_x$ と $\psi$ は以下のようにして求めます。
\begin{aligned}
{B_x}_M &= {B_x}_L+\frac{1}{2}\left({B_x}_R-{B_x}_L\right)-\frac{1}{2c_h}\left(\psi_R-\psi_L\right) \\
\psi_M &= \psi_L+\frac{1}{2}\left(\psi_R-\psi_L\right)-\frac{c_h}{2}\left({B_x}_R-{B_x}_L\right)
\end{aligned}
実際の計算においては $\psi$ のソース項をそのまま計算するのではなく、一旦ソース項を忘れて他変数と同様にフラックスの差から $\psi^*$ を求めた後、以下のようにして $\psi^{n+1}$ を求めるのが一般的です。
\psi^{n+1} = \psi^*\exp\left(-\Delta t_n\frac{c_h^2}{c_p^2}\right)
なおここで出てくる $c_h$ と $c_p$ は、$\nabla\cdot\mathbf{B}$ および $\psi$ に対する人工的な伝播と減衰の速さを表すフリーパラメータになります。
$c_h$ としてはCFL条件によって許される最大速度、
c_h = \mathrm{CFL}\cdot\mathrm{min}\left(\Delta x, \Delta y, \Delta z\right)/\Delta t_n
$c_p$ としては $c_r = c_p^2/c_h$ が定数となるようにした上で、$c_r = 0.18$ を選ぶのが空間解像度によらず最適となるようです。
高精度化
$\mathbf{F}_{i+1/2}$ を求める際、$\mathbf{U}_L$ として $\mathbf{U}_i$ を、$\mathbf{U}_R$ として $\mathbf{U}_{i+1}$ を選ぶのはいわゆる風上差分に相当し、1次の空間精度になります。
後で図をお見せしますが、実はこれ、数値拡散が大きくかなりぼやけた解になります。そこでここでは空間精度を上げる方法を紹介します。
また時間精度についても、常微分方程式でRunge-Kutta法を用いることで精度が上げられたように、偏微分方程式でも同様のことを考えることができます。
(そろそろ長くなって疲れてきました。。。)
空間の高精度化
${\mathbf{U}_{i+1/2}}_L$ として例えば
{\mathbf{U}_{i+1/2}}_L = \frac{-\mathbf{U}_{i-1}+4\mathbf{U}_i+\mathbf{U}_{i+1}}{4}
を使うようにすれば空間2次精度が得られますが、このように $\mathbf{U}$ を単純に線形に組み合わせるだけだと数値振動が発生してしまいあまり好ましくありません。
そこでこれを回避するために様々な非線形スキームが考案されています。ここでは2次精度のMUSCLと5次精度のMP5を簡単に紹介します。
MUSCL
van Leer (1979) で提案された手法で、以下のようにリミッターを導入することで基本は2次精度を保ちつつ、不連続面では数値振動が発生しないように1次精度に落とすことができます。
\begin{aligned}
{\mathbf{U}_{i+1/2}}_L &= \mathbf{U}_i+\frac{1}{2}\Delta_i \\
{\mathbf{U}_{i-1/2}}_R &= \mathbf{U}_i-\frac{1}{2}\Delta_i
\end{aligned}
\Delta_i = \mathrm{limiter}\left(\mathbf{U}_{i+1}-\mathbf{U}_i, \mathbf{U}_i-\mathbf{U}_{i-1}\right)
リミッターとしては以下のminmod (Roe, 1986) やMC (van Leer, 1977) がよく使われるようです。
\begin{aligned}
\mathrm{minmod}\left(a, b\right) &= \frac{1}{2}\left[\mathrm{sign}\left(a\right)+\mathrm{sign}\left(b\right)\right]\mathrm{min}\left(|a|, |b|\right) \\
\mathrm{MC}\left(a, b\right) &= \frac{1}{2}\left[\mathrm{sign}\left(a\right)+\mathrm{sign}\left(b\right)\right]\mathrm{min}\left(2|a|, \frac{|a+b|}{2}, 2|b|\right)
\end{aligned}
MP5
Suresh and Huynh (1997) による方法です。まず ${\mathbf{U}_{i+1/2}}_L$ を5次精度の線形スキームで補間します。
{\mathbf{U}_{i+1/2}}^*_L = \frac{2\mathbf{U}_{i-2}-13\mathbf{U}_{i-1}+47\mathbf{U}_i+27\mathbf{U}_{i+1}-3\mathbf{U}_{i+2}}{60}
もちろんこのままでは数値振動が発生してしまうため、ある下限値 $\mathbf{U}_{\mathrm{min}}$ と上限値 $\mathbf{U}_{\mathrm{max}}$ を定め、それらの中央値を使って ${\mathbf{U}_{i+1/2}}_L$ を求めます。
{\mathbf{U}_{i+1/2}}_L = \mathrm{median}\left({\mathbf{U}_{i+1/2}}^*_L, \mathbf{U}_{\mathrm{min}}, \mathbf{U}_{\mathrm{max}}\right)
具体的な $\mathbf{U}_{\mathrm{min}}$ と $\mathbf{U}_{\mathrm{max}}$ の求め方は結構長いのでここでは省略します。
時間の高精度化
\frac{d\mathbf{U}}{dt} = L\left(\mathbf{U}\right)
と書けるとき、以下のように解くのはいわゆるオイラー法に相当し、1次の時間精度になります。
\mathbf{U}^{n+1} = \mathbf{U}^n+\Delta tL\left(\mathbf{U}^n\right)
しかしこれもRunge-Kutta法を使えば精度を上げることができます。
今回はRunge-Kutta法のうちでも、特に余分な数値振動を発生させないという意味で性質の良いSSPRK (strong stability preserving Runge-Kutta) シリーズ (Shu and Osher, 1988) を載せておきます。
2次精度 SSPRK (2, 2)
\begin{aligned}
\mathbf{U}^{\left(1\right)} &= \mathbf{U}^n+\Delta tL\left(\mathbf{U}^n\right) \\
\mathbf{U}^{n+1} &= \frac{1}{2}\mathbf{U}^n+\frac{1}{2}\mathbf{U}^{\left(1\right)}+\frac{1}{2}\Delta tL\left(\mathbf{U}^{\left(1\right)}\right)
\end{aligned}
3次精度 SSPRK (3, 3)
\begin{aligned}
\mathbf{U}^{\left(1\right)} &= \mathbf{U}^n+\Delta tL\left(\mathbf{U}^n\right) \\
\mathbf{U}^{\left(2\right)} &= \frac{3}{4}\mathbf{U}^n+\frac{1}{4}\mathbf{U}^{\left(1\right)}+\frac{1}{4}\Delta tL\left(\mathbf{U}^{\left(1\right)}\right) \\
\mathbf{U}^{n+1} &= \frac{1}{3}\mathbf{U}^n+\frac{2}{3}\mathbf{U}^{\left(2\right)}+\frac{2}{3}\Delta tL\left(\mathbf{U}^{\left(2\right)}\right)
\end{aligned}
結果
以上を踏まえて、MP5およびSSPRK (3, 3)を用いて計算した結果が以下になります。以下はすべて分割数 $N_x\times N_y = 200\times 200$, $\mathrm{CFL} = 0.4$ で計算しています。
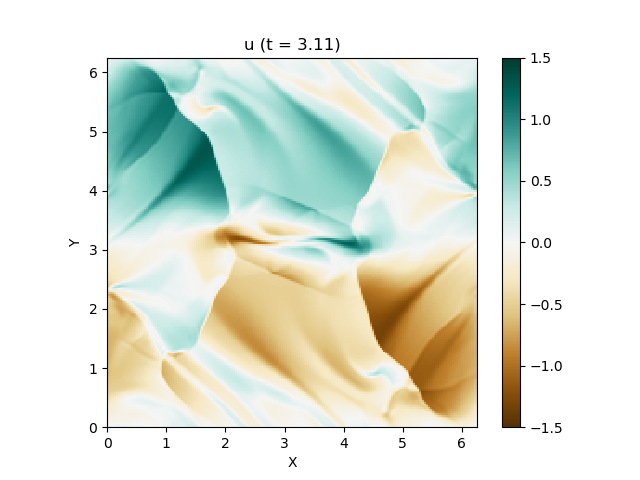
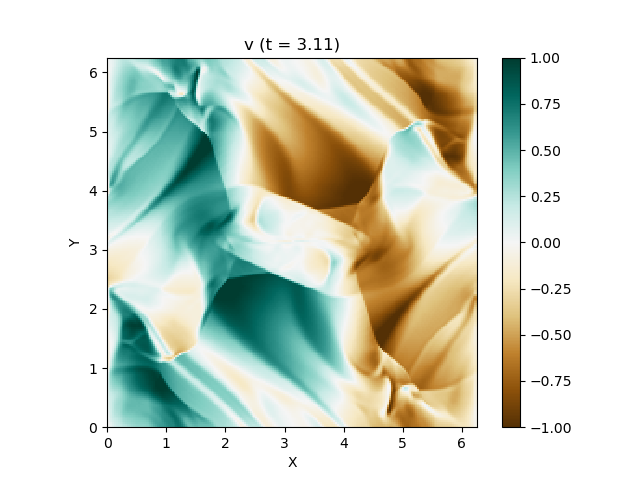
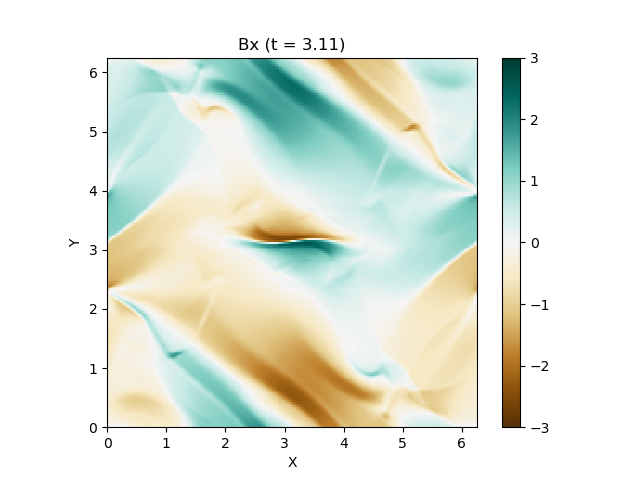
上は圧力のプロットです。折り畳んだところを開けばすべての変数が見られます。
良い感じ!
スキームによる違い
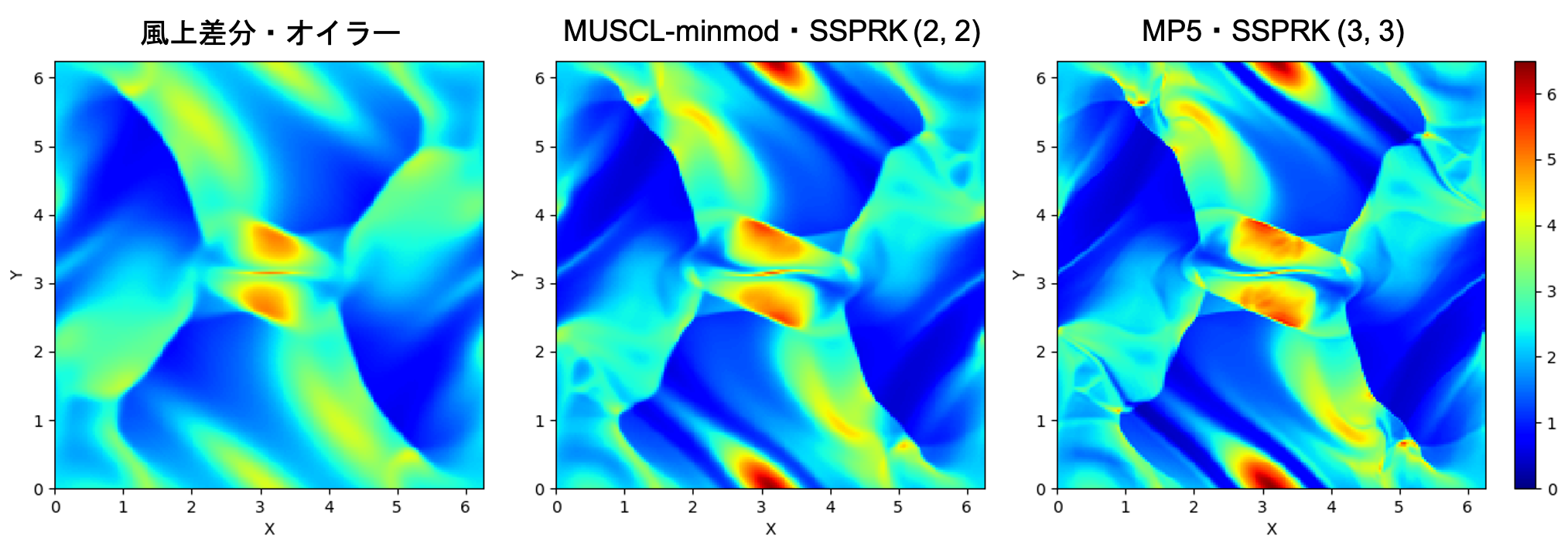
せっかくなのでスキームによる違いも見てみましょう。以下の3種類を比較してみます。
- 風上差分・オイラー法 (空間1次・時間1次)
- MUSCL-minmod・SSPRK (2, 2) (空間2次・時間2次)
- MP5・SSPRK (3, 3) (空間5次・時間3次)
こうしてみると歴然とした違いがありますね。特に風上差分・オイラー法は同じ空間解像度のはずなのに随分ぼやけてしまっています。
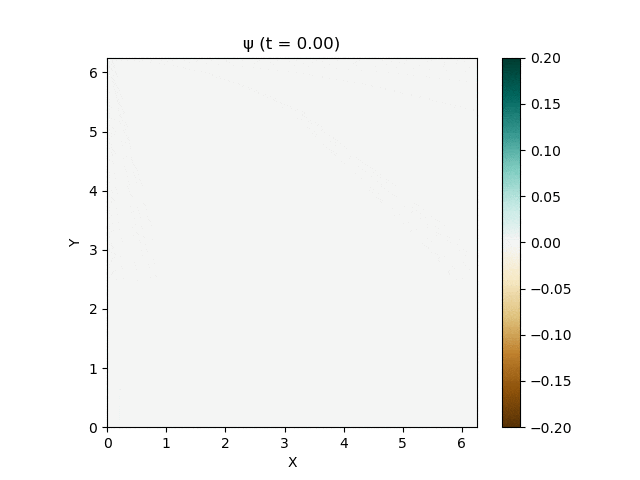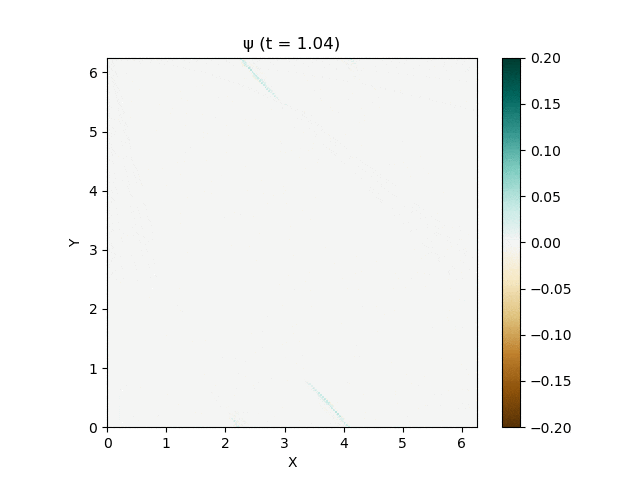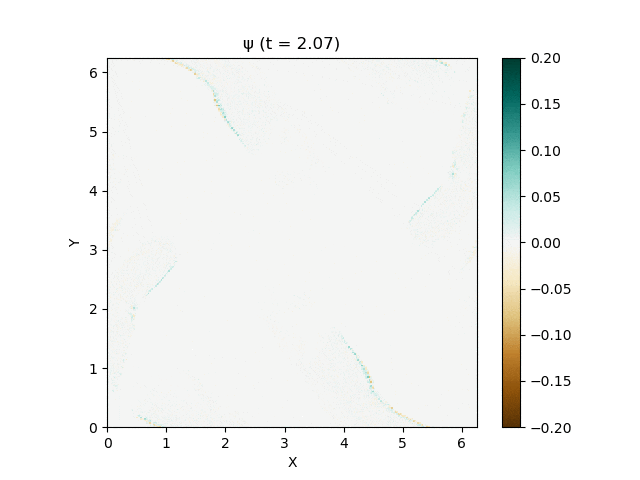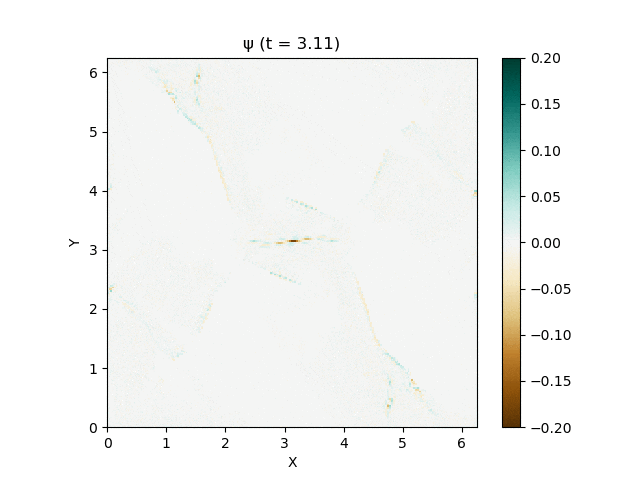
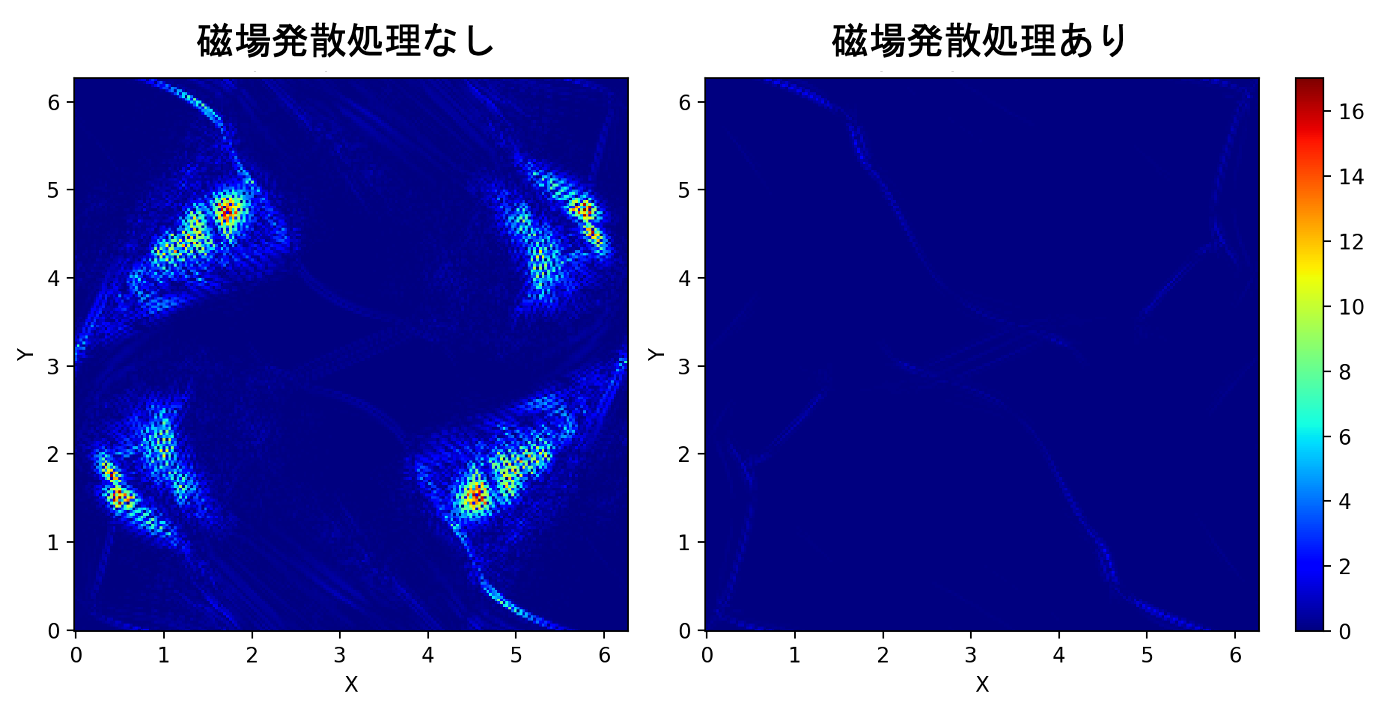
磁場発散処理の有無による違い
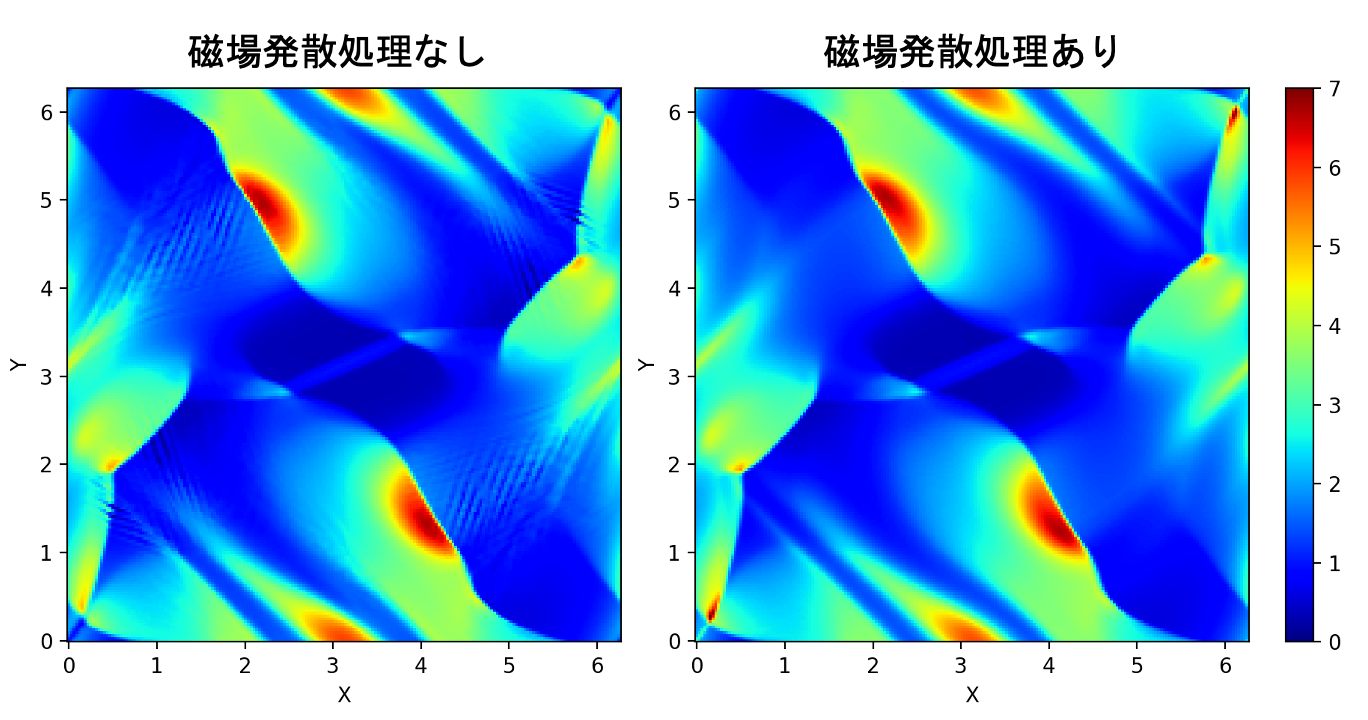
次に磁場発散処理を入れなかったらどうなるか見てみます。
両者の違いが一番見やすかったMUSCL-minmod・SSPRK (2, 2)で比較します。
...
...
磁場発散処理を入れないと破綻してしまいました。。。
とりあえず計算が壊れる直前の図を見比べてみます。
左にはいかにもヤバそうな、怪しい縞模様が見えますね。
$|\nabla\cdot\mathbf{B}|$ をプロットしてみると、ちょうどそこで大きな磁場発散が生じてしまっていることがわかります。一方で右ではうまく抑えられていますね。
ソースコード
現時点でC++とPythonの2バージョンを作成しており、GutHubにて公開しています。
C++バージョンではOpenMPによる並列化を施しているので、$N_x\times N_y = 200\times 200$ のような大きなサイズの計算に適しています。なお、constexpr if文や構造化束縛を使っているのでコンパイルにはC++17以上が必要です。
一方Pythonバージョンではその場ですぐプロットするように作ったので、サクッと結果を見たい場合はこちらが良いかと思います。Pythonといってもfor文を排除してできるだけNumPyに計算を任せるようにしているので、そこそこのパフォーマンスになってくれる、はず。。。
長くなるのでここではPythonバージョンのみ載せておきます。
Pythonバージョンのソースコード
import time
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# グリッド数
# XN = 200; YN = 200
XN = 100; YN = 100
# ファイル出力回数
PN = 100
# 保存変数の個数
VN = 9
# 計算領域のサイズ
XL = 2.0*np.pi; YL = 2.0*np.pi
TL = np.pi
# グリッドサイズ
dx = XL/XN; dy = YL/YN
# CFL数
CFL = 0.4
# 比熱比
gam = 5.0/3.0
# 磁場発散抑制のためのパラメータ (Dedner et al., 2002)
cr = 0.18
# MINMOD関数
def minmod(a, b):
return 0.5*(np.sign(a)+np.sign(b))*np.minimum(np.abs(a), np.abs(b))
# 中央値
def median(a, b, c):
return a+minmod(b-a, c-a)
# x方向フラックス
def mhdfx(rho, u, v, w, bx, by, bz, e, psi, pt, ch):
fx = np.zeros((XN, YN, VN))
fx[:, :, 0] = rho*u
fx[:, :, 1] = rho*u*u+pt-bx*bx
fx[:, :, 2] = rho*v*u-bx*by
fx[:, :, 3] = rho*w*u-bx*bz
fx[:, :, 4] = psi
fx[:, :, 5] = by*u-bx*v
fx[:, :, 6] = bz*u-bx*w
fx[:, :, 7] = (e+pt)*u-bx*(u*bx+v*by+w*bz)
fx[:, :, 8] = ch*ch*bx
return fx
# y方向フラックス
def mhdfy(rho, u, v, w, bx, by, bz, e, psi, pt, ch):
fy = np.zeros((XN, YN, VN))
fy[:, :, 0] = rho*v
fy[:, :, 1] = rho*u*v-by*bx
fy[:, :, 2] = rho*v*v+pt-by*by
fy[:, :, 3] = rho*w*v-by*bz
fy[:, :, 4] = bx*v-by*u
fy[:, :, 5] = psi
fy[:, :, 6] = bz*v-by*w
fy[:, :, 7] = (e+pt)*v-by*(u*bx+v*by+w*bz)
fy[:, :, 8] = ch*ch*by
return fy
# HLLDリーマンソルバ (Miyoshi and Kusano, 2005)
def hlldx(ql, qr, ch):
# 密度
rhol = ql[:, :, 0]
rhor = qr[:, :, 0]
# 運動量
mxl = ql[:, :, 1]
myl = ql[:, :, 2]
mzl = ql[:, :, 3]
mxr = qr[:, :, 1]
myr = qr[:, :, 2]
mzr = qr[:, :, 3]
# 磁場
bxl = ql[:, :, 4]
byl = ql[:, :, 5]
bzl = ql[:, :, 6]
bxr = qr[:, :, 4]
byr = qr[:, :, 5]
bzr = qr[:, :, 6]
# エネルギー
el = ql[:, :, 7]
er = qr[:, :, 7]
# 磁場発散抑制のための人工ポテンシャル (Dedner et al., 2002)
psil = ql[:, :, 8]
psir = qr[:, :, 8]
# 速度
ul = mxl/rhol
vl = myl/rhol
wl = mzl/rhol
ur = mxr/rhor
vr = myr/rhor
wr = mzr/rhor
# (熱的) 圧力
pl = (gam-1.0)*(el-0.5*rhol*(ul*ul+vl*vl+wl*wl)-0.5*(bxl*bxl+byl*byl+bzl*bzl))
pr = (gam-1.0)*(er-0.5*rhor*(ur*ur+vr*vr+wr*wr)-0.5*(bxr*bxr+byr*byr+bzr*bzr))
ptl = pl+0.5*(bxl*bxl+byl*byl+bzl*bzl)
# 総圧力 (熱的圧力 + 磁気圧)
ptr = pr+0.5*(bxr*bxr+byr*byr+bzr*bzr)
# 音速
al = np.sqrt(gam*pl/rhol)
ar = np.sqrt(gam*pr/rhor)
# Alfvén速度
cal = np.sqrt((bxl*bxl+byl*byl+bzl*bzl)/rhol)
car = np.sqrt((bxr*bxr+byr*byr+bzr*bzr)/rhor)
caxl = np.sqrt(bxl*bxl/rhol)
caxr = np.sqrt(bxr*bxr/rhor)
# 速進磁気音波速度
cfl = np.sqrt(0.5*(al*al+cal*cal+np.sqrt((al*al+cal*cal)**2-4.0*(al*caxl)**2)))
cfr = np.sqrt(0.5*(ar*ar+car*car+np.sqrt((ar*ar+car*car)**2-4.0*(ar*caxr)**2)))
sfl = np.minimum(ul-cfl, ur-cfr)
sfr = np.maximum(ul+cfl, ur+cfr)
sm = ((sfr-ur)*rhor*ur-(sfl-ul)*rhol*ul-ptr+ptl)/((sfr-ur)*rhor-(sfl-ul)*rhol)
um = sm
bxm = bxl+0.5*(bxr-bxl)-0.5/ch*(psir-psil)
psim = psil+0.5*(psir-psil)-0.5*ch*(bxr-bxl)
# リーマンファン外側
ptm = ((sfr-ur)*rhor*ptl-(sfl-ul)*rhol*ptr+rhol*rhor*(sfr-ur)*(sfl-ul)*(ur-ul))/((sfr-ur)*rhor-(sfl-ul)*rhol)
rhoml = rhol*(sfl-ul)/(sfl-sm)
rhomr = rhor*(sfr-ur)/(sfr-sm)
vol = vl-bxm*byl*(sm-ul)/(rhol*(sfl-ul)*(sfl-sm)-bxm*bxm)
vor = vr-bxm*byr*(sm-ur)/(rhor*(sfr-ur)*(sfr-sm)-bxm*bxm)
wol = wl-bxm*bzl*(sm-ul)/(rhol*(sfl-ul)*(sfl-sm)-bxm*bxm)
wor = wr-bxm*bzr*(sm-ur)/(rhor*(sfr-ur)*(sfr-sm)-bxm*bxm)
byol = byl*(rhol*(sfl-ul)*(sfl-ul)-bxm*bxm)/(rhol*(sfl-ul)*(sfl-sm)-bxm*bxm)
byor = byr*(rhor*(sfr-ur)*(sfr-ur)-bxm*bxm)/(rhor*(sfr-ur)*(sfr-sm)-bxm*bxm)
bzol = bzl*(rhol*(sfl-ul)*(sfl-ul)-bxm*bxm)/(rhol*(sfl-ul)*(sfl-sm)-bxm*bxm)
bzor = bzr*(rhor*(sfr-ur)*(sfr-ur)-bxm*bxm)/(rhor*(sfr-ur)*(sfr-sm)-bxm*bxm)
eol = ((sfl-ul)*el-ptl*ul+ptm*sm+bxm*(ul*bxl+vl*byl+wl*bzl-um*bxm-vol*byol-wol*bzol))/(sfl-sm)
eor = ((sfr-ur)*er-ptr*ur+ptm*sm+bxm*(ur*bxr+vr*byr+wr*bzr-um*bxm-vor*byor-wor*bzor))/(sfr-sm)
srrhoml = np.sqrt(rhoml)
srrhomr = np.sqrt(rhomr)
sal = sm-np.sqrt(bxm*bxm/rhoml)
sar = sm+np.sqrt(bxm*bxm/rhomr)
# リーマンファン内側
vi = (srrhoml*vol+srrhomr*vor+(byor-byol)*np.sign(bxm))/(srrhoml+srrhomr)
wi = (srrhoml*wol+srrhomr*wor+(bzor-bzol)*np.sign(bxm))/(srrhoml+srrhomr)
byi = (srrhoml*byor+srrhomr*byol+srrhoml*srrhomr*(vor-vol)*np.sign(bxm))/(srrhoml+srrhomr)
bzi = (srrhoml*bzor+srrhomr*bzol+srrhoml*srrhomr*(wor-wol)*np.sign(bxm))/(srrhoml+srrhomr)
eil = eol-srrhoml*(vol*byol+wol*bzol-vi*byi-wi*bzi)*np.sign(bxm)
eir = eor+srrhomr*(vor*byor+wor*bzor-vi*byi-wi*bzi)*np.sign(bxm)
fxl = mhdfx(rhol, ul, vl, wl, bxm, byl, bzl, el, psim, ptl, ch)
fxol = mhdfx(rhoml, um, vol, wol, bxm, byol, bzol, eol, psim, ptm, ch)
fxil = mhdfx(rhoml, um, vi, wi, bxm, byi, bzi, eil, psim, ptm, ch)
fxir = mhdfx(rhomr, um, vi, wi, bxm, byi, bzi, eir, psim, ptm, ch)
fxor = mhdfx(rhomr, um, vor, wor, bxm, byor, bzor, eor, psim, ptm, ch)
fxr = mhdfx(rhor, ur, vr, wr, bxm, byr, bzr, er, psim, ptr, ch)
fx = np.zeros((XN, YN, VN))
slindex = sfl > 0.0
solindex = (0.0 >= sfl) & (sal > 0.0)
silindex = (0.0 >= sal) & (sm > 0.0)
sirindex = (0.0 >= sm) & (sar > 0.0)
sorindex = (0.0 >= sar) & (sfr > 0.0)
srindex = 0.0 >= sfr
fx[slindex, :] = fxl[slindex, :]
fx[solindex, :] = fxol[solindex, :]
fx[silindex, :] = fxil[silindex, :]
fx[sirindex, :] = fxir[sirindex, :]
fx[sorindex, :] = fxor[sorindex, :]
fx[srindex, :] = fxr[srindex, :]
return fx
def hlldy(ql, qr, ch):
# 密度
rhol = ql[:, :, 0]
rhor = qr[:, :, 0]
# 運動量
mxl = ql[:, :, 1]
myl = ql[:, :, 2]
mzl = ql[:, :, 3]
mxr = qr[:, :, 1]
myr = qr[:, :, 2]
mzr = qr[:, :, 3]
# 磁場
bxl = ql[:, :, 4]
byl = ql[:, :, 5]
bzl = ql[:, :, 6]
bxr = qr[:, :, 4]
byr = qr[:, :, 5]
bzr = qr[:, :, 6]
# エネルギー
el = ql[:, :, 7]
er = qr[:, :, 7]
# 磁場発散抑制のための人工ポテンシャル (Dedner et al., 2002)
psil = ql[:, :, 8]
psir = qr[:, :, 8]
# 速度
ul = mxl/rhol
vl = myl/rhol
wl = mzl/rhol
ur = mxr/rhor
vr = myr/rhor
wr = mzr/rhor
# (熱的) 圧力
pl = (gam-1.0)*(el-0.5*rhol*(ul*ul+vl*vl+wl*wl)-0.5*(bxl*bxl+byl*byl+bzl*bzl))
pr = (gam-1.0)*(er-0.5*rhor*(ur*ur+vr*vr+wr*wr)-0.5*(bxr*bxr+byr*byr+bzr*bzr))
# 総圧力 (熱的圧力 + 磁気圧)
ptl = pl+0.5*(bxl*bxl+byl*byl+bzl*bzl)
ptr = pr+0.5*(bxr*bxr+byr*byr+bzr*bzr)
# 音速
al = np.sqrt(gam*pl/rhol)
ar = np.sqrt(gam*pr/rhor)
# Alfvén速度
cal = np.sqrt((bxl*bxl+byl*byl+bzl*bzl)/rhol)
car = np.sqrt((bxr*bxr+byr*byr+bzr*bzr)/rhor)
cayl = np.sqrt(byl*byl/rhol)
cayr = np.sqrt(byr*byr/rhor)
# 速進磁気音波速度
cfl = np.sqrt(0.5*(al*al+cal*cal+np.sqrt((al*al+cal*cal)**2-4.0*(al*cayl)**2)))
cfr = np.sqrt(0.5*(ar*ar+car*car+np.sqrt((ar*ar+car*car)**2-4.0*(ar*cayr)**2)))
sfl = np.minimum(vl-cfl, vr-cfr)
sfr = np.maximum(vl+cfl, vr+cfr)
sm = ((sfr-vr)*rhor*vr-(sfl-vl)*rhol*vl-ptr+ptl)/((sfr-vr)*rhor-(sfl-vl)*rhol)
vm = sm
bym = byl+0.5*(byr-byl)-0.5/ch*(psir-psil)
psim = psil+0.5*(psir-psil)-0.5*ch*(byr-byl)
# リーマンファン外側
ptm = ((sfr-vr)*rhor*ptl-(sfl-vl)*rhol*ptr+rhol*rhor*(sfr-vr)*(sfl-vl)*(vr-vl))/((sfr-vr)*rhor-(sfl-vl)*rhol)
rhoml = rhol*(sfl-vl)/(sfl-sm)
rhomr = rhor*(sfr-vr)/(sfr-sm)
wol = wl-bym*bzl*(sm-vl)/(rhol*(sfl-vl)*(sfl-sm)-bym*bym)
wor = wr-bym*bzr*(sm-vr)/(rhor*(sfr-vr)*(sfr-sm)-bym*bym)
uol = ul-bym*bxl*(sm-vl)/(rhol*(sfl-vl)*(sfl-sm)-bym*bym)
uor = ur-bym*bxr*(sm-vr)/(rhor*(sfr-vr)*(sfr-sm)-bym*bym)
bzol = bzl*(rhol*(sfl-vl)*(sfl-vl)-bym*bym)/(rhol*(sfl-vl)*(sfl-sm)-bym*bym)
bzor = bzr*(rhor*(sfr-vr)*(sfr-vr)-bym*bym)/(rhor*(sfr-vr)*(sfr-sm)-bym*bym)
bxol = bxl*(rhol*(sfl-vl)*(sfl-vl)-bym*bym)/(rhol*(sfl-vl)*(sfl-sm)-bym*bym)
bxor = bxr*(rhor*(sfr-vr)*(sfr-vr)-bym*bym)/(rhor*(sfr-vr)*(sfr-sm)-bym*bym)
eol = ((sfl-vl)*el-ptl*vl+ptm*sm+bym*(ul*bxl+vl*byl+wl*bzl-uol*bxol-vm*bym-wol*bzol))/(sfl-sm)
eor = ((sfr-vr)*er-ptr*vr+ptm*sm+bym*(ur*bxr+vr*byr+wr*bzr-uor*bxor-vm*bym-wor*bzor))/(sfr-sm)
srrhoml = np.sqrt(rhoml)
srrhomr = np.sqrt(rhomr)
sal = sm-np.sqrt(bym*bym/rhoml)
sar = sm+np.sqrt(bym*bym/rhomr)
# リーマンファン内側
wi = (srrhoml*wol+srrhomr*wor+(bzor-bzol)*np.sign(bym))/(srrhoml+srrhomr)
ui = (srrhoml*uol+srrhomr*uor+(bxor-bxol)*np.sign(bym))/(srrhoml+srrhomr)
bzi = (srrhoml*bzor+srrhomr*bzol+srrhoml*srrhomr*(wor-wol)*np.sign(bym))/(srrhoml+srrhomr)
bxi = (srrhoml*bxor+srrhomr*bxol+srrhoml*srrhomr*(uor-uol)*np.sign(bym))/(srrhoml+srrhomr)
eil = eol-srrhoml*(uol*bxol+wol*bzol-ui*bxi-wi*bzi)*np.sign(bym)
eir = eor+srrhomr*(uor*bxor+wor*bzor-ui*bxi-wi*bzi)*np.sign(bym)
fyl = mhdfy(rhol, ul, vl, wl, bxl, bym, bzl, el, psim, ptl, ch)
fyol = mhdfy(rhoml, uol, vm, wol, bxol, bym, bzol, eol, psim, ptm, ch)
fyil = mhdfy(rhoml, ui, vm, wi, bxi, bym, bzi, eil, psim, ptm, ch)
fyir = mhdfy(rhomr, ui, vm, wi, bxi, bym, bzi, eir, psim, ptm, ch)
fyor = mhdfy(rhomr, uor, vm, wor, bxor, bym, bzor, eor, psim, ptm, ch)
fyr = mhdfy(rhor, ur, vr, wr, bxr, bym, bzr, er, psim, ptr, ch)
fy = np.zeros((XN, YN, VN))
slindex = sfl > 0.0
solindex = (0.0 >= sfl) & (sal > 0.0)
silindex = (0.0 >= sal) & (sm > 0.0)
sirindex = (0.0 >= sm) & (sar > 0.0)
sorindex = (0.0 >= sar) & (sfr > 0.0)
srindex = 0.0 >= sfr
fy[slindex, :] = fyl[slindex, :]
fy[solindex, :] = fyol[solindex, :]
fy[silindex, :] = fyil[silindex, :]
fy[sirindex, :] = fyir[sirindex, :]
fy[sorindex, :] = fyor[sorindex, :]
fy[srindex, :] = fyr[srindex, :]
return fy
# 1次精度風上差分
def upwindx(q):
qil = np.roll(q, 1, axis = 0)
qi = q
ql = qil
qr = qi
return ql, qr
def upwindy(q):
qjl = np.roll(q, 1, axis = 1)
qj = q
ql = qjl
qr = qj
return ql, qr
# 2次精度MUSCL (minmod) (van Leer, 1979)
def musclx(q):
qill = np.roll(q, 2, axis = 0)
qil = np.roll(q, 1, axis = 0)
qi = q
qir = np.roll(q, -1, axis = 0)
ql = qil+0.5*minmod(qi-qil, qil-qill)
qr = qi-0.5*minmod(qir-qi, qi-qil)
return ql, qr
def muscly(q):
qjll = np.roll(q, 2, axis = 1)
qjl = np.roll(q, 1, axis = 1)
qj = q
qjr = np.roll(q, -1, axis = 1)
ql = qjl+0.5*minmod(qj-qjl, qjl-qjll)
qr = qj-0.5*minmod(qjr-qj, qj-qjl)
return ql, qr
# 5次精度MP5 (Suresh and Huynh, 1997)
def mp5x(q):
qilll = np.roll(q, 3, axis = 0)
qill = np.roll(q, 2, axis = 0)
qil = np.roll(q, 1, axis = 0)
qi = q
qir = np.roll(q, -1, axis = 0)
qirr = np.roll(q, -2, axis = 0)
dll = qilll-2.0*qill+qil
dl = qill-2.0*qil+qi
d = qil-2.0*qi+qir
dr = qi-2.0*qir+qirr
dmml = minmod(dll, dl)
dmm = minmod(dl, d)
dmmr = minmod(d, dr)
qull = qil+2.0*(qil-qill)
qulr = qi+2.0*(qi-qir)
#qull = qil+4.0*(qil-qill)
#qulr = qi+4.0*(qi-qir)
qav = 0.5*(qil+qi)
qmd = qav-0.5*dmm
qlcl = qil+0.5*(qil-qill)+4.0/3.0*dmml
qlcr = qi+0.5*(qi-qir)+4.0/3.0*dmmr
qminl = np.maximum(np.minimum(qil, qi, qmd), np.minimum(qil, qull, qlcl))
qmaxl = np.minimum(np.maximum(qil, qi, qmd), np.maximum(qil, qull, qlcl))
qminr = np.maximum(np.minimum(qi, qil, qmd), np.minimum(qi, qulr, qlcr))
qmaxr = np.minimum(np.maximum(qi, qil, qmd), np.maximum(qi, qulr, qlcr))
q5l = (2.0*qilll-13.0*qill+47.0*qil+27.0*qi-3.0*qir)/60.0
q5r = (2.0*qirr-13.0*qir+47.0*qi+27.0*qil-3.0*qill)/60.0
ql = median(q5l, qminl, qmaxl)
qr = median(q5r, qminr, qmaxr)
return ql, qr
def mp5y(q):
qjlll = np.roll(q, 3, axis = 1)
qjll = np.roll(q, 2, axis = 1)
qjl = np.roll(q, 1, axis = 1)
qj = q
qjr = np.roll(q, -1, axis = 1)
qjrr = np.roll(q, -2, axis = 1)
dll = qjlll-2.0*qjll+qjl
dl = qjll-2.0*qjl+qj
d = qjl-2.0*qj+qjr
dr = qj-2.0*qjr+qjrr
dmml = minmod(dll, dl)
dmm = minmod(dl, d)
dmmr = minmod(d, dr)
qull = qjl+2.0*(qjl-qjll)
qulr = qj+2.0*(qj-qjr)
#qull = qjl+4.0*(qjl-qjll)
#qulr = qj+4.0*(qj-qjr)
qav = 0.5*(qjl+qj)
qmd = qav-0.5*dmm
qlcl = qjl+0.5*(qjl-qjll)+4.0/3.0*dmml
qlcr = qj+0.5*(qj-qjr)+4.0/3.0*dmmr
qminl = np.maximum(np.minimum(qjl, qj, qmd), np.minimum(qjl, qull, qlcl))
qmaxl = np.minimum(np.maximum(qjl, qj, qmd), np.maximum(qjl, qull, qlcl))
qminr = np.maximum(np.minimum(qj, qjl, qmd), np.minimum(qj, qulr, qlcr))
qmaxr = np.minimum(np.maximum(qj, qjl, qmd), np.maximum(qj, qulr, qlcr))
q5l = (2.0*qjlll-13.0*qjll+47.0*qjl+27.0*qj-3.0*qjr)/60.0
q5r = (2.0*qjrr-13.0*qjr+47.0*qj+27.0*qjl-3.0*qjll)/60.0
ql = median(q5l, qminl, qmaxl)
qr = median(q5r, qminr, qmaxr)
return ql, qr
# dq/dtの計算
def dqdt(q, ch):
# x方向
#ql, qr = upwindx(q)
#ql, qr = musclx(q)
ql, qr = mp5x(q)
fx = hlldx(ql, qr, ch)
# y方向
#ql, qr = upwindy(q)
#ql, qr = muscly(q)
ql, qr = mp5y(q)
fy = hlldy(ql, qr, ch)
# 保存則の計算
fxi = fx
fyj = fy
fxir = np.roll(fx, -1, axis = 0)
fyjr = np.roll(fy, -1, axis = 1)
dqdt = -(fxir-fxi)/dx-(fyjr-fyj)/dy
return dqdt
# 1次精度Euler法
def euler(q, dt):
ch = CFL*np.minimum(dx, dy)/dt
q1 = q+dqdt(q, ch)*dt
return q1
# 2次精度Runge-Kutta
def ssprk2(q, dt):
ch = CFL*np.minimum(dx, dy)/dt
q1 = q+dqdt(q, ch)*dt
q2 = 0.5*q+0.5*(q1+dqdt(q1, ch)*dt)
return q2
# 3次精度Runge-Kutta
def ssprk3(q, dt):
ch = CFL*np.minimum(dx, dy)/dt
q1 = q+dqdt(q, ch)*dt
q2 = 0.75*q+0.25*(q1+dqdt(q1, ch)*dt)
q3 = 1.0/3.0*q+2.0/3.0*(q2+dqdt(q2, ch)*dt)
return q3
def main():
# rho: 密度
# p: 圧力
# u: x方向速度
# v: y方向速度
# w: z方向速度
# mx: x方向運動量
# my: y方向運動量
# mz: z方向運動量
# bx: x方向磁場
# by: y方向磁場
# bz: z方向磁場
# e: エネルギー
# psi: 磁場発散抑制のための人工ポテンシャル (Dedner et al., 2002)
# q: 保存変数ベクトル
# -- 0: rho
# -- 1: mx
# -- 2: my
# -- 3: mz
# -- 4: bx
# -- 5: by
# -- 6: bz
# -- 7: e
# -- 8: psi
x = np.arange(0.0, XL, dx)
y = np.arange(0.0, YL, dy)
# 初期値
rho = np.ones((XN, YN))*gam**2
p = np.ones((XN, YN))*gam
u = np.tile(-np.sin(y), (XN, 1))
v = np.tile(np.sin(x), (YN, 1)).T
w = np.zeros((XN, YN))
bx = np.tile(-np.sin(y), (XN, 1))
by = np.tile(np.sin(2.0*x), (YN, 1)).T
bz = np.zeros((XN, YN))
e = p/(gam-1.0)+0.5*rho*(u*u+v*v+w*w)+0.5*(bx*bx+by*by+bz*bz)
psi = np.zeros((XN, YN))
q = np.zeros((XN, YN, VN)); q_n = np.zeros((XN, YN, VN))
q[:, :, 0] = rho
q[:, :, 1] = rho*u
q[:, :, 2] = rho*v
q[:, :, 3] = rho*w
q[:, :, 4] = bx
q[:, :, 5] = by
q[:, :, 6] = bz
q[:, :, 7] = e
q[:, :, 8] = psi
# 計算開始
n = 0
t = 0.0
step = 0
start = time.time()
while (t <= TL):
# 密度
rho = q[:, :, 0]
# 運動量
mx = q[:, :, 1]
my = q[:, :, 2]
mz = q[:, :, 3]
# 磁場
bx = q[:, :, 4]
by = q[:, :, 5]
bz = q[:, :, 6]
# エネルギー
e = q[:, :, 7]
# 磁場発散抑制のための人工ポテンシャル (Dedner et al., 2002)
psi = q[:, :, 8]
# 速度
u = mx/rho
v = my/rho
w = mz/rho
# (熱的) 圧力
p = (gam-1.0)*(e-0.5*rho*(u*u+v*v+w*w)-0.5*(bx*bx+by*by+bz*bz))
# 音速
a = np.sqrt(gam*p/rho)
# Alfvén速度
ca = np.sqrt((bx*bx+by*by+bz*bz)/rho)
cax = np.sqrt(bx*bx/rho)
cay = np.sqrt(by*by/rho)
# 速進磁気音波速度
cfx = np.sqrt(0.5*(a*a+ca*ca+np.sqrt((a*a+ca*ca)**2-4.0*(a*cax)**2)))
cfy = np.sqrt(0.5*(a*a+ca*ca+np.sqrt((a*a+ca*ca)**2-4.0*(a*cay)**2)))
# CFL数をもとにdtを設定
dt = CFL*np.minimum(dx/np.max(np.abs(u)+cfx), dy/np.max(np.abs(v)+cfy))
# 磁場発散抑制のためのパラメータ (Dedner et al., 2002)
ch = CFL*np.minimum(dx, dy)/dt
cd = np.exp(-dt*ch/cr)
# 時間発展
#q_n = euler(q, dt)
#q_n = ssprk2(q, dt)
q_n = ssprk3(q, dt)
q_n[:, :, 8] = cd*q_n[:, :, 8]
q = q_n
# ファイル出力
if (np.floor(t*PN/TL) != np.floor((t-dt)*PN/TL)) :
print("n: {0:3d}, t: {1:.2f}".format(n, t))
#varname = ["r", "p", "u", "v", "w", "bx", "by", "bz", "ps"]
#vardata = [rho, p, u, v, w, bx, by, bz, psi]
#for i in range(VN):
# np.savetxt("../data/"+varname[i]+"_{0:0>3}.csv".format(n), vardata[i].T, delimiter = ",")
n += 1
t += dt
step += 1
elapsed_time = time.time()-start
print("elapsed_time: {0} s".format(elapsed_time))
# 計算終了
# 計算失敗の検知
if (not np.isfinite(t)):
print("Computaion failed: step = {0:3d}".format(step))
# y = πでの値
print(" x rho p u v w bx by bz psi")
for i in range(0, XN, 5):
j = YN//2
print("{0:4.2f} {1:5.2f} {2:5.2f} {3:5.2f} {4:5.2f} {5:5.2f} {6:5.2f} {7:5.2f} {8:5.2f} {9:5.2f}"
.format(dx*i, rho[i, j], p[i, j], u[i, j], v[i, j], w[i, j], bx[i, j], by[i, j], bz[i, j], psi[i, j]))
# 結果をプロット
fig = plt.figure()
plt.axes().set_aspect("equal")
plt.title("p (t = {0:.2f})".format(t))
plt.xlabel("X")
plt.ylabel("Y")
im = plt.pcolor(x, y, p.T, cmap = cm.jet, shading = "auto")
im.set_clim(0.0, 6.5)
fig.colorbar(im)
plt.show()
if __name__ == "__main__":
main()
参考文献
- Orszag, S., & Tang, C. (1979). Small-scale structure of two-dimensional magnetohydrodynamic turbulence. Journal of Fluid Mechanics, 90(1), 129-143. doi:10.1017/S002211207900210X
- Takahiro Miyoshi, Kanya Kusano, A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics, Journal of Computational Physics, Volume 208, Issue 1, 2005, Pages 315-344, ISSN 0021-9991, https://doi.org/10.1016/j.jcp.2005.02.017.
- A. Dedner, F. Kemm, D. Kröner, C.-D. Munz, T. Schnitzer, M. Wesenberg, Hyperbolic Divergence Cleaning for the MHD Equations,Journal of Computational Physics, Volume 175, Issue 2, 2002, Pages 645-673, ISSN 0021-9991, https://doi.org/10.1006/jcph.2001.6961.
- Bram van Leer, Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method, Journal of Computational Physics, Volume 32, Issue 1, 1979, Pages 101-136, ISSN 0021-9991, https://doi.org/10.1016/0021-9991(79)90145-1.
- Roe, P L, Characteristic-Based Schemes for the Euler Equations, Annual Review of Fluid Mechanics, Volume 18, 337-365, 1986, https://doi.org/10.1146/annurev.fl.18.010186.002005
- Bram Van Leer, Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow, Journal of Computational Physics, Volume 23, Issue 3, 1977, Pages 263-275, ISSN 0021-9991, https://doi.org/10.1016/0021-9991(77)90094-8.
- A. Suresh, H.T. Huynh, Accurate Monotonicity-Preserving Schemes with Runge–Kutta Time Stepping, Journal of Computational Physics, Volume 136, Issue 1, 1997, Pages 83-99, ISSN 0021-9991, https://doi.org/10.1006/jcph.1997.5745.
- Chi-Wang Shu, Stanley Osher, Efficient implementation of essentially non-oscillatory shock-capturing schemes, Journal of Computational Physics, Volume 77, Issue 2, 1988, Pages 439-471, ISSN 0021-9991, https://doi.org/10.1016/0021-9991(88)90177-5.
また、今回の記事執筆に際し、以下のページを全般に渡って参考にしています。