はじめに
当初は申し込みが必要、Python2.7 のみ対応しており、速度はそこまで早くない。
だけど環境構築しないで jupyter notebook 使えるのは良いよね、という扱いだった(気がする) Google colaboratory ですが、 Python3 に対応し GPU, TPU を搭載することでかなりのいけぽよサービスになっています。
やはり機械学習の分野で注目を集めていますが、colaboratory の GPU で並列計算を行えば数値シミュレーションもスルッと行けるのでは?ということを思いつきましたので、簡単な粒子系の数値計算をCuPyを用いて実装し、速度比べをしてみました。
要素の相互作用が行列で書けさえすれば基本的には別の系にも適用できるはずです。
Python は独学で数ヶ月というレベルなので、ご指導ご鞭撻いただければ幸いです。
問題設定
2次元平面上にランダムに分布している $n$ 個の質点(座標は $\vec{u_i}$ で表される)が、以下の式に応じて相互作用した場合の平衡状態を計算する。
\frac{d}{dt}\vec{u_i} = \sum_{j=1}^{n} f(r_{i,j}) \left( \vec{u_j}-\vec{u_i} \right) \\
f(r) =
\begin{cases}
-4 \left( r-\frac{3}{2} \right)^2 +1 & (0<x<1.6) \\
0 & \text{(otherwise)}
\end{cases}
ここでの $r_{i,j}$ は質点 $i$ と質点 $j$ との距離を表し、$i$ と $j$ は $1$ から $n$ までの整数が入ります。
小難しく書いていますが、結局は
- 質点間の距離が 1.6 以下であればその2点は相互作用する
- 1以下であれば斥力が働き、1より大きければ引力が働く
という程度です。各質点とその相互作用については細胞集団ですとか、動物の縄張りですとかをイメージしていただければと思います。後者に引力が働くかは知らないですけど。また、$f$の形についてはかなり適当です。
設定
Google colaboratory の初めの登録などは詳しい記事がたくさん出ているのでそちらをご参照ください。Google のアカウントを普段から使っている方でしたら秒で億稼ぐ男が 300 億稼ぐ間くらいに終わると思います。
無事 colaboratory の notebook 画面に到達しましたら ランタイム → ランタイムのタイプを変更 として、ハードウェアアクセラレータを GPU に変更して保存を押してみてください。
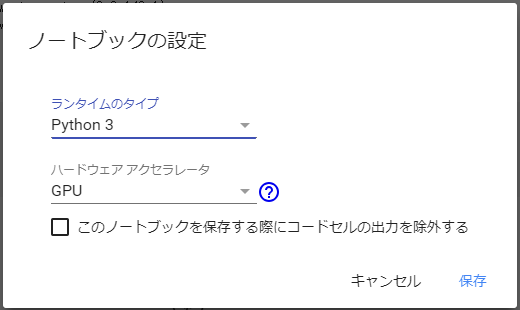
これで notebook が GPU で動くようになります。
CuPy の導入
CuPy は numpy.~~ をそのまま cupy.~~ と切り替えるだけで GPU 用のコードになるという非常に優れたライブラリです。機械学習ライブラリの Chainer において用いられているそうです。詳しいことはこちらをご参照ください。
そういう事情もあってか、 Chainer をインストールすると一緒に CuPy も導入できるのでそちらを行います。Chainer を開発した Preferred Networks も現代のハイカラ企業の一部ですが、そこはイケてる者同士、以下の Linux コマンドを notebook の cell に打ち込み実行するだけで自動的に 60 秒程度で Chainer, CuPy がインストールされます。
!curl https://colab.chainer.org/install | sh -
インストールが終わりましたら、続いて各種必要なライブラリを import しましょう。
import cupy as cp
import numpy as np
import time
import chainer
numpy は標準でインストールされているので、 import のみで問題ないです。今回は numpy と cupy との速度比べに興味があるので、その都合で time も import しています。chainer も import した方が良いとこちらに書いてあったので一応しています。
ここまでくれば準備は完了です。
計算する
まずは関数 $f$ を表す def を作ります。この際、各配列に対する関数を定義して map 関数を使うという流れだと list 形式にしたり array 形式にしたりとしんどそう(& 遅そう)だったので、可能な限り numpy.array および cupy.array のまま処理できるように設計します。
def repn1(x): #numpy用
y1 = x <= 1.6
z1 = -(4*(x-1.5)**2-1) * y1.astype(np.int)
return z1
def repc1(x): #cupy用
y1 = x <= 1.6
z1 = -(4*(x-1.5)**2-1) * y1.astype(cp.int)
return z1
本当に np を cp に変えただけなのですが、きちんと動いてくれます。
では早速、以下のパラメータを用いて計算してみます。
dt=0.01
cellN=1000
numpy での計算
x=np.random.rand(cellN)*65
y=np.random.rand(cellN)*65
start = time.time()
for i in range(1000):
xn=x.reshape(1,cellN)
xt=x.reshape(cellN,1)
firx=np.power(xn,2)
secx=np.power(xt,2)
thix=np.dot(xt,xn)
xx2=firx+secx-2*thix #broadcast を利用
yn=y.reshape(1,cellN)
yt=y.reshape(cellN,1)
firy=np.power(yn,2)
secy=np.power(yt,2)
thiy=np.dot(yt,yn)
yy2=firy+secy-2*thiy #broadcast を利用
norm=np.sqrt(np.abs(xx2+yy2))
f1 = repn1(norm)+np.diag(8*np.ones(cellN))
f2=np.diag(np.sum(f1,1))
res=f1-f2 #作用部分
x=x+dt*np.dot(res,x)
y=y+dt*np.dot(res,y)
elapsed_time = time.time() - start
print ("elapsed_time:{0}".format(elapsed_time) + "[sec]")
計算の要点としては…
- 各質点の$x$座標と$y$座標が配列の形で格納されている。
- 各座標成分の初期値は $[0,65]$ の一様乱数により決定する。
- 質点 $i$ と $j$ との間の距離 $r_{i,j}$ を $i,j$ 成分とする行列 (norm) を計算する。
- norm の各要素に関数 $f$ を適用し、ベクトル $\vec{x}$, $\vec{y}$ との dot 積を取ることで微小変位を計算できるような 相互作用行列 (res) を計算する。
- $dt$ 経過後の質点の座標を新しい $x$, $y$ とし、これを繰り返す。
という程度のものです。今回は 1000 ループ行いました。
結果としては 57.055 sec (アクセラレータが GPU の場合)、 51.967 sec (アクセラレータが CPU の場合) でした。
CuPy での計算
同様に CuPy でも計算してみます。こちらについては、 NumPy のコードにおける np を cp に交換するだけなので非常に楽です。
x=cp.random.rand(cellN)*65
y=cp.random.rand(cellN)*65
start = time.time()
for i in range(1000):
xn=x.reshape(1,cellN)
xt=x.reshape(cellN,1)
firx=cp.power(xn,2)
secx=cp.power(xt,2)
thix=cp.dot(xt,xn)
xx2=firx+secx-2*thix #broadcast を利用
yn=y.reshape(1,cellN)
yt=y.reshape(cellN,1)
firy=cp.power(yn,2)
secy=cp.power(yt,2)
thiy=cp.dot(yt,yn)
yy2=firy+secy-2*thiy #broadcast を利用
norm=cp.sqrt(cp.abs(xx2+yy2))
f1 = repc1(norm)+cp.diag(8*cp.ones(cellN))
f2 = cp.diag(cp.sum(f1,1))
res=f1-f2 #作用部分
x=x+dt*cp.dot(res,x)
y=y+dt*cp.dot(res,y)
elapsed_time = time.time() - start
print ("elapsed_time:{0}".format(elapsed_time) + "[sec]")
こちらでは結果は 10.374 sec でした。
結果とまとめ
計算は同様ですが、$n$ を動かしてみて多少まとめました(軽量化のため 100 ループ)。
- numpy
- $n$ = 100; 0.040 sec
- $n$ = 1000; 5.255 sec
- $n$ = 2000; 23.27 sec
- $n$ = 4000; 96.68 sec
- cupy
- $n$ = 100; 0.589 sec (0.068倍高速化)
- $n$ = 1000; 0.615 sec (8.545倍高速化)
- $n$ = 2000; 0.947 sec (24.57倍高速化)
- $n$ = 4000; 3.502 sec (27.61倍高速化)
やはり要素数というか、配列の大きさが大きい場合には圧倒的に GPU の方が早くなりますね。
ということで、要素数は多いが、挙動自体は比較的単純なシミュレーションの場合は試してみてはいかがでしょう。
C++ などと比べてどうか、などについては今後の課題とさせていただきたく存じます。
追記: line_profiler による分析
line_profiler というものを知ったので、これを使ってどの計算が律速になっているかを見てみました。
参考:こちら
!pip install line_profiler
%load_ext line_profiler
def func(cellN):
x=cp.random.rand(cellN)*65
y=cp.random.rand(cellN)*65
for i in range(1000):
xn=x.reshape(1,cellN)
xt=x.reshape(cellN,1)
firx=cp.power(xn,2)
secx=cp.power(xt,2)
thix=cp.dot(xt,xn)
xx2=firx+secx-2*thix #broadcast を利用
yn=y.reshape(1,cellN)
yt=y.reshape(cellN,1)
firy=cp.power(yn,2)
secy=cp.power(yt,2)
thiy=cp.dot(yt,yn)
yy2=firy+secy-2*thiy #broadcast を利用
norm=cp.sqrt(cp.abs(xx2+yy2))
f1 = repc1(norm)+cp.diag(8*cp.ones(cellN))
f2 = cp.diag(cp.sum(f1,1))
res=f1-f2 #作用部分
x=x+dt*cp.dot(res,x)
y=y+dt*cp.dot(res,y)
dt=0.01
%lprun -f func func(1000)
Google colab で使う場合には、以上のように pip コマンドでインストールする必要があります。ただ、これも20秒程度で終わるのでそんなに面倒ではないです。
結果です
Line # Hits Time Per Hit % Time Line Contents
==============================================================
1 def func(cellN):
2 1 1679.0 1679.0 0.0 x=cp.random.rand(cellN)*65
3 1 636.0 636.0 0.0 y=cp.random.rand(cellN)*65
4 1001 2031.0 2.0 0.0 for i in range(1000):
5 1000 6478.0 6.5 0.1 xn=x.reshape(1,cellN)
6 1000 4012.0 4.0 0.0 xt=x.reshape(cellN,1)
7 1000 303770.0 303.8 3.3 firx=cp.power(xn,2)
8 1000 303689.0 303.7 3.3 secx=cp.power(xt,2)
9 1000 60410.0 60.4 0.7 thix=cp.dot(xt,xn)
10 1000 872779.0 872.8 9.4 xx2=firx+secx-2*thix #broadcast を利用
11
12 1000 7069.0 7.1 0.1 yn=y.reshape(1,cellN)
13 1000 4483.0 4.5 0.0 yt=y.reshape(cellN,1)
14 1000 303737.0 303.7 3.3 firy=cp.power(yn,2)
15 1000 301412.0 301.4 3.2 secy=cp.power(yt,2)
16 1000 59585.0 59.6 0.6 thiy=cp.dot(yt,yn)
17 1000 869992.0 870.0 9.4 yy2=firy+secy-2*thiy #broadcast を利用
18
19 1000 818036.0 818.0 8.8 norm=cp.sqrt(cp.abs(xx2+yy2))
20 1000 3341997.0 3342.0 36.0 f1 = repc1(norm)+cp.diag(8*cp.ones(cellN))
21 1000 437992.0 438.0 4.7 f2 = cp.diag(cp.sum(f1,1))
22 1000 283326.0 283.3 3.1 res=f1-f2 #作用部分
23
24 1000 651754.0 651.8 7.0 x=x+dt*cp.dot(res,x)
25 1000 641799.0 641.8 6.9 y=y+dt*cp.dot(res,y)
これを見ると、行20で非線形な関数を行列にかけるあたりで時間を使っているようです。そのため、 repc1 の形がもっとスマートに記述出来たらより早くなると思われます。他にも、broad cast や sqrt, abs をかけるあたりで時間がかかっていることが分かります。