はじめに
シクシク素数列 Advent Calendar 2018を見てて気づいてしまった
誰も「あの」解法を採っていないことに
なので自分でやります
言語はすでにC++を使っている人がいましたが、とある理由(後述)で自分もC++を用いることにします
シクシク素数列 - C++編
ルール
数値に4か9を含む素数をシクシク素数と呼ぶことにします
19とか41とか149とか。
標準入力として正の整数 N を与えたら N 番目までのシクシク素数を半角カンマ区切りで標準出力してください
例 N = 9 の場合、 19,29,41,43,47,59,79,89,97
N は最大で 100 とします
素直な解法
# include <algorithm>
# include <cmath>
# include <iostream>
# include <vector>
bool check_p49(int x) {
while (x) {
switch (x % 10) {
case 4:
case 9:
return true;
default:
x /= 10;
}
}
return false;
}
int main() {
int n;
std::cin >> n;
n = std::min(n, 100);
std::vector<int> table;
table.reserve(1024);
table.push_back(2);
for (int count = 0, i = 3; count < n; i += 2) {
int lim = std::sqrt(i);
bool p = true;
for (auto x : table) {
if (!(i % x)) {
p = false;
break;
}
if (lim < x) {
break;
}
}
if (!p) {
continue;
}
table.push_back(i);
if (check_p49(i)) {
std::cout << i << (n - count - 1 ? "," : "\n");
++count;
}
}
return 0;
}
素直に篩にかける
解法(おふざけ)
この問題、出力する素数の種類は常に同じで、その個数だけが違う
問題文には「素数を篩などで探せ」という文言はない
また、N<=100という条件がある
なので、次のソースコードでも正しい出力を得られる
# include <iostream>
int main()
{
int p4949[100] = {19, 29, 41, 43, 47, 59, 79, 89, 97, 109, 139, 149, 179, 191, 193, 197, 199, 229, 239, 241, 269, 293, 347, 349, 359, 379, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 509, 541, 547, 569, 593, 599, 619, 641, 643, 647, 659, 691, 709, 719, 739, 743, 769, 797, 809, 829, 839, 859, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1019, 1039, 1049, 1069, 1091, 1093, 1097, 1109, 1129, 1193, 1229, 1249, 1259, 1279, 1289, 1291, 1297, 1319};
int n;
std::cin >> n;
n = std::min(n, 100);
for (int i = 0; i < n; ++i)
{
std::cout << p4949[i] << (n - i - 1 ? "," : "\n");
}
return 0;
}
素数判定に用いられるエラトステネスの篩の計算量が$O(NloglogN)$らしいですが、このプログラムでは$O(N)$で解を出力できます
おふざけ解法その2
# include <iostream>
int main()
{
char p4949[100][10] = {"19,", "29,", "41,", "43,", "47,", "59,", "79,", "89,", "97,", "109,", "139,", "149,", "179,", "191,", "193,", "197,", "199,", "229,", "239,", "241,", "269,", "293,", "347,", "349,", "359,", "379,", "389,", "397,", "401,", "409,", "419,", "421,", "431,", "433,", "439,", "443,", "449,", "457,", "461,", "463,", "467,", "479,", "487,", "491,", "499,", "509,", "541,", "547,", "569,", "593,", "599,", "619,", "641,", "643,", "647,", "659,", "691,", "709,", "719,", "739,", "743,", "769,", "797,", "809,", "829,", "839,", "859,", "907,", "911,", "919,", "929,", "937,", "941,", "947,", "953,", "967,", "971,", "977,", "983,", "991,", "997,", "1009,", "1019,", "1039,", "1049,", "1069,", "1091,", "1093,", "1097,", "1109,", "1129,", "1193,", "1229,", "1249,", "1259,", "1279,", "1289,", "1291,", "1297,", "1319,"};
int n;
std::cin >> n;
n = std::min(n, 100);
for (int i = 0; i < n; ++i)
{
if (i + 1 != n)
{
std::cout << p4949[i];
}
else
{
auto s = std::string_view(p4949[i]);
s.remove_suffix(1);
std::cout << s << std::endl;
}
}
return 0;
}
数値から文字列に変換するコストを嫌ってみる
おふざけ解法その3
# include <iostream>
int main()
{
char p4949[] = {"19,29,41,43,47,59,79,89,97,109,139,149,179,191,193,197,199,229,239,241,269,293,347,349,359,379,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,509,541,547,569,593,599,619,641,643,647,659,691,709,719,739,743,769,797,809,829,839,859,907,911,919,929,937,941,947,953,967,971,977,983,991,997,1009,1019,1039,1049,1069,1091,1093,1097,1109,1129,1193,1229,1249,1259,1279,1289,1291,1297,1319,"};
size_t end[100] = {3, 6, 9, 12, 15, 18, 21, 24, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99, 103, 107, 111, 115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163, 167, 171, 175, 179, 183, 187, 191, 195, 199, 203, 207, 211, 215, 219, 223, 227, 231, 235, 239, 243, 247, 251, 255, 259, 263, 267, 271, 275, 279, 283, 287, 291, 295, 299, 303, 307, 311, 315, 320, 325, 330, 335, 340, 345, 350, 355, 360, 365, 370, 375, 380, 385, 390, 395, 400, 405, 410};
int n;
std::cin >> n;
n = std::min(n, 100);
std::cout << std::string_view(p4949).substr(0, end[n - 1] - 1) << std::endl;
return 0;
}
最初から文字列を1つにつなげてみた
配列endにはN番目の4949素数の文字列の終端位置が入っている
計測
とりあえず処理時間を計測してみる
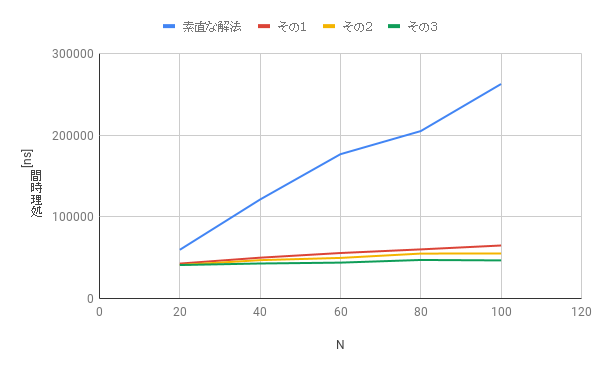
...まあそうなるよね
(なんか縦軸のラベルの文字が90度回ってるけど気にしない(Google Spread Sheetさんがんばって))
しかし
このプログラムは明らかに仕様変更に弱い
突然4949じゃなくて5959がいいなんて言われたら他のプログラム(もしくは手動)でほしい素数列を列挙する必要がある
でもよく考えてみればC++には他の言語にはない最強の武器があるじゃないか
素数列をコンパイル時に生成しちゃえばいいじゃないか
というわけでおふざけ解法で使った配列をコンパイル時に生成する
# include <algorithm>
# include <array>
# include <cmath>
# include <iostream>
# include <vector>
constexpr bool check_p49(int x) {
while (x) {
switch (x % 10) {
case 4:
case 9:
return true;
default:
x /= 10;
}
}
return false;
}
constexpr std::array<int, 100> make_p4949_sequence() {
std::array<int, 100> result{};
for (int count = 0, i = 3; count < result.size(); i += 2) {
bool p = true;
for (int j = 2; j <= std::sqrt(i); ++j) {
if (!(i % j)) {
p = false;
break;
}
}
if (!p) {
continue;
}
if (check_p49(i)) {
result[count++] = i;
}
}
return result;
}
int main() {
int n;
std::cin >> n;
n = std::min(n, 100);
constexpr auto p4949 = make_p4949_sequence();
for (int i = 0; i < n; ++i) {
std::cout << p4949[i] << (n - i - 1 ? "," : "\n");
}
return 0;
}
これでおふざけ解法その1と同じパフォーマンスが得られる
その2その3も同様にできると思うけど、コンパイル時の文字列操作とかめんどくさすぎてやりたくない
追記
どうやらstd::sqrtのconstexpr版はGCCの独自拡張らしいので、それ以外のコンパイラではsprout::sqrtなどに置き換えてください
ループの上限を$\sqrt N$にしなくてもコンパイルが遅くなるだけだし別にいいかなとか思ったり