はじめに
前職の業務で遺伝的アルゴリズムを用いた数理最適化を行っており、その際にPythonの進化計算ライブラリDEAPを用いる機会があったので実装例をまとめておきたいと思いました。
DEAPを用いた実数値遺伝的アルゴリズムの実装例はネットで探しても見かけなかったので、役に立てば良いなと思います。
遺伝的アルゴリズム(Genetic Algorithm, GA)
遺伝的アルゴリズムは自然淘汰の仕組みを最適化問題に応用したアルゴリズムです。
生命進化の場合、周囲の自然環境に適応できた個体の遺伝子は子孫へと受け継がれ、適応できなかった個体の染色体は受け継がれずに途絶えてしまいます。また、突然変異などにより他の個体よりも環境への適応度の高い個体が生まれた場合は、その遺伝子はより子孫へと受け継がれやすくなります。これらが繰り返されることで、環境への適応度が高い個体が最終的に残ります。これが自然淘汰のメカニズムです。
遺伝的アルゴリズムでは解きたい問題の解の候補(個体)をランダムに生成して多数の個体からなる個体集団を作成します。個体集団内の個体に対して交叉(2つの個体から新しい個体を生成する操作)や変異(個体をランダムに変更する操作)といった操作を行い適応度(問題における解の良さ)の高い個体を選出します。これら一連の操作を繰り返し実行することで集団内の個体は淘汰されていき、最終的に最適解を得る事ができます。
問題設定
解きたい問題
本記事ではDEAPに入っているベンチマーク関数Ackleyの2次元空間における最小値の探索を行います。
Ackley関数
関数式は以下です。
f(x, y) = 20 - 20\exp\Biggl(-0.2\sqrt{\frac{x^2 + y^2}{2}}\Biggl) + e - \exp\Biggl(\frac{\cos(2\pi x) + \cos(2\pi y)}{2}\Biggl)
この関数を3次元プロットしたものが下図です。
公式ドキュメントでは変数の定義域は[-15, 30]となっていましたが、今回は[-500, 500]とします。
左図は[-30, 30]の範囲で、右図は[-500, 500]の範囲で表示しています。

図を見て分かる通り曲面が非常にギザギザしており、(x, y)=(0, 0)において最小値0.0を取る関数です。
(公式ドキュメント, Ackley関数)
https://deap.readthedocs.io/en/master/api/benchmarks.html
遺伝子
個体の遺伝子は解の候補となる2次元空間上の点のx, y座標とします。
また個体遺伝子はそれぞれ[-500, 500]の範囲で一様に生成します。
交叉
交叉はブレンド交叉(BLX-α)を用います。
ブレンド交叉では下図のように親子体によってできる矩形領域に対して各軸を1+2α倍した矩形領域内で一様に次世代個体候補を生成します。
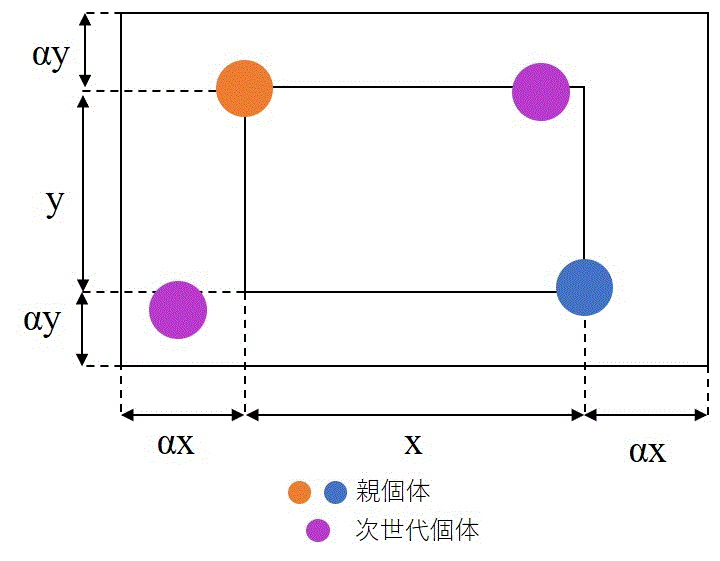
変異
変異はガウス変異を用います。
個体に変異を行う際には個体の遺伝子に、指定した平均値、分散のガウス分布から発生した乱数が加算されます。
個体選択
トーナメント方式による個体選択を行います。
トーナメント方式では指定された個数の個体が集団からランダムに選出され、その中で最良の個体が次世代個体の候補となります。ランダムに選出される個体数はトーナメントサイズと呼ばれます。
実行環境
- Python 3.7.3
- deap 1.2
実装
実装コード : https://github.com/t-yoshitake/ga-sample/blob/master/ga.py
実装は公式ドキュメントにあるOne Max Problem(バイナリ値の最適化問題)の実装をベースに実数値関数の最小値探索を行うように修正しています。
(One Max Problemの実装コード https://deap.readthedocs.io/en/master/examples/ga_onemax.html)
コードの解説
import random
from deap import base, creator, tools
from deap.benchmarks import ackley
まず最初にDEAPモジュールのインポートを行っています。
今回用いるベンチマーク関数はackleyとして読み込んでいます。
# 適応度クラスの作成
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creatorはclass factoryというもので、createメソッドにより指定した名前、親クラス、属性を持つクラスを作成します。
creator.createの引数は順に、作成するクラス名、継承するクラス、クラスの属性第1、第2引数は必須で第3以降の引数は任意です。
base.Fitnessは抽象クラスであり、weights属性を必ずオーバーライドする必要があります。
なのでここではweightsが必須になります。
weightsはタプルで渡します。
関数値を最小化する場合は(-1.0, )、最大化する場合は(1.0, )。サイズが2以上のタプルを渡すことで複数の関数の最適化ができるようです。
# 個体クラスの作成
creator.create("Individual", list, fitness=creator.FitnessMin)
ここでは個体クラスIndividualを作成しています。Individualはlistクラスを継承し、先程作成したcreator.FitnessMinを属性として持ちます。
# Toolboxの作成
toolbox = base.Toolbox()
Toolboxには様々な関数を指定した名前で登録することができます。
ここでは以下の関数を登録します。
- attr_gene : 遺伝子を生成する関数
- individual : 個体を生成する関数
- population : 個体集団を生成する関数
- evaluate : 評価関数
- mate : 交叉を実行する関数
- mutate : 変異を実行する関数
- select : 次世代の個体を選択する関数
# 遺伝子を生成する関数"attr_gene"を登録
toolbox.register("attr_gene", random.uniform, -500, 500)
toolbox.registerで関数の登録を行っています。引数は順に関数の登録名、登録する関数、登録する関数の引数(任意)です。
上の例では遺伝子を生成する関数の登録を行っており、初期個体の遺伝子を-500から500の間でランダムに作成するために一様乱数を生成する関数random.uniformと引数を登録しています。
# 個体を生成する関数”individual"を登録
toolbox.register("individual", tools.initRepeat, creator.Individual,
toolbox.attr_gene, 2)
個体を生成する関数の登録を行っています。tools.initRepeatの引数としてcreator.Individual, toolbox.attr_gene, 2を登録しています。tools.initRepeatはtoolbox.attr_geneを2回実行することでcreator.Individualクラスを初期化します。
今回の問題では個体は2つの遺伝子を持ち、各遺伝子が2次元空間上の点のx, y座標に対応するように設定しています。
# 個体集団を生成する関数"population"を登録
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
個体集団を生成する関数の登録を行っています。上で定義したtoolbox.inidividualを繰り返し実行する処理を行っていますが、繰り返し回数(集団内の個体数)は実行時に引数として指定したいため、登録時には指定していません。
# 評価関数"evaluate"を登録
toolbox.register("evaluate", ackley)
個体の評価関数の登録を行っています。
# 交叉を行う関数"mate"を登録
toolbox.register("mate", tools.cxBlend, alpha=0.2)
交叉を実行する関数の登録を行っています。
cxBlendはブレンド交叉を行う関数で、第1, 2引数が交叉対象の個体、第3引数が交叉パラメータαになります。
ここでは交叉パラメータを指定し、対象個体は実行時に指定します。
# 変異を行う関数"mutate"を登録
toolbox.register("mutate", tools.mutGaussian, mu=[
0.0, 0.0], sigma=[200.0, 200.0], indpb=0.2)
変異を実行する関数の登録を行っています。
mutGaussianは個体にガウス変異を加える関数で、引数は順に対象個体、ガウス分布の平均値(mu)、ガウス分布の標準偏差(sigma)、独立変異確率(indpb)です。ここで独立変異確率は個体の1つの遺伝子に変異がかかる確率です。ここでも対象個体は指定せずに実行時に引数として与えます。
# 個体選択法"select"を登録
toolbox.register("select", tools.selTournament, tournsize=3)
個体選択を実行する関数の登録を行っています。
selTournamentは個体選択を行う関数で対象個体集団、選択個体数、トーナメントサイズ(tournsize)を引数として受けます。
ここではトーナメントサイズを指定し、対象個体集団、選択個体数は実行時に指定します。
def main():
random.seed(1)
# GAパラメータ
N_GEN = 100 # 繰り返し世代数
POP_SIZE = 1000 # 集団内の個体数
CX_PB = 0.5 # 交叉確率
MUT_PB = 0.2 # 変異確率
ここからmain関数の説明に入ります。
GAの制御のためのパラメータを定義しています。
# 個体集団の生成
pop = toolbox.population(n=POP_SIZE)
print("Start of evolution")
# 個体集団の適応度の評価
fitnesses = list(map(toolbox.evaluate, pop))
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(pop))
# 適応度の抽出
fits = [ind.fitness.values[0] for ind in pop]
ここで記述した処理は進化ループ処理に入る前の前処理です。
まず個体集団の生成を行っています。個体の生成はtoolboxに登録した関数"population"に集団内の個体数POP_SIZEを渡して実行しています。
個体は前に定義したIndividualクラスのインスタンスですが、生成時はfitness属性が設定されていないので2段目の処理で各個体のfitness属性を設定しています。設定する値はtoolboxに登録した関数"evaluate"の出力値(個体を引数としたackley関数の出力値)です。
最後の段の処理では各個体の適応度を抽出しリスト化しています。
# 進化ループ開始
g = 0
while g < N_GEN:
g = g + 1
print("-- Generation %i --" % g)
# 次世代個体の選択・複製
offspring = toolbox.select(pop, len(pop))
offspring = list(map(toolbox.clone, offspring))
進化ループに入ります。
上記コードの最後の2行の1行目は次世代に引き継ぐ個体の選択を行うためにtoolbox.selectを実行しています。
しかしこのままではoffspringはpop内の個体への参照となっているので、2行目で参照を切ることでoffspringをpopとは独立したコピーとして作成しています。
# 交叉
for child1, child2 in zip(offspring[::2], offspring[1::2]):
# 交叉させる個体を選択
if random.random() < CX_PB:
toolbox.mate(child1, child2)
# 交叉させた個体は適応度を削除する
del child1.fitness.values
del child2.fitness.values
交叉処理の部分です。
次世代個体候補から個体を2個ずつ選択肢、確率CX_PBで個体同士の交叉を行っています。
交叉を実行した個体のfitness属性は後で再設定するために一旦削除しています。
# 変異
for mutant in offspring:
# 変異させる個体を選択
if random.random() < MUT_PB:
toolbox.mutate(mutant)
# 変異させた個体は適応度を削除する
del mutant.fitness.values
変異処理を行っています。
# 適応度を削除した個体について適応度の再評価を行う
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(invalid_ind))
# 個体集団を新世代個体集団で更新
pop[:] = offspring
交叉あるいは変異を行った個体は遺伝子が変化しているので、適応度(fitness属性)を再評価する必要があります。
上記の部分ではfitness属性の再設定を行い、個体集団popを次世代の個体集団offspringで更新しています。
# 新世代の全個体の適応度の抽出
fits = [ind.fitness.values[0] for ind in pop]
# 適応度の統計情報の出力
length = len(pop)
mean = sum(fits) / length
sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print(" Min %s" % min(fits))
print(" Max %s" % max(fits))
print(" Avg %s" % mean)
print(" Std %s" % std)
ここでは各世代の全個体について適応度を抽出し、統計情報を出力しています。
以上で進化ループ処理は終わりです。
# 最良個体の抽出
best_ind = tools.selBest(pop, 1)[0]
print("Best individual is %s, %s" % (best_ind, best_ind.fitness.values))
最後に最終世代の個体集団内の最良個体を抽出し、遺伝子と適応度を出力しています。
結果
繰り返し世代数100, 集団内個体数1000で実行した結果、最終世代の最良個体は(x, y)=(-4.014e-17, 7.845e-17)でこのときのackley関数値は0.0となりました。
また、進化過程の結果を図示したものが下です。個体分布のヒストグラムをヒートマップ図で表しており横軸がx座標遺伝子、縦軸がy座標遺伝子に対応しヒストグラムのカウント数を0から最大10までを色付けしています(赤い所ほど個体が密集しています)。ヒートマップ図は1, 5, 10, 20, 100世代目の結果を出力しています。最初はまばらに生成された個体が世代を経るごとに最適解(0, 0)密集していることがわかります。最後の図は集団内個体のfitness値の最小値を世代ごとにプロットしたもので(横軸:世代、縦軸:fitness最小値)、20世代くらいでfitnessの最小値はほぼ0となっており、最小値探索は上手くいったことがわかります。
条件を厳しくして探索がうまくいくかやってみました。先の例では初期個体を[-500, 500]の範囲で一様に生成していましたが、個体生成の座標の範囲を[400, 500]に変更しました。また実行条件は繰り返し世代数20000, 集団内個体数1000でその他の条件は同じです。結果は最終世代の最良個体は(x, y)=(1.892e-17, -3.985e-17)で関数値は0.0となり、最小値を求めることができました。
下図は第1, 20000世代のヒストグラムとfitnessの最小値の世代推移図です。

その他
-
探索したい領域が有限領域の場合は、個体遺伝子が探索区間から外れた場合に適応度を大幅に悪くすることで探索区間に制限をかけることができます。DEAPにはそのためのメソッドが用意されており、簡単に制限をかけることができます。
https://deap.readthedocs.io/en/master/tutorials/advanced/constraints.html?highlight=constraint -
実際の業務ではもっと複雑な最適化問題を扱っていて、良い解が得られるハイパーパラメータ(繰り返し世代数、集団内個体数、交叉確率、変異確率など)を探すのに苦労しました。この辺はディープラーニングでも用いられているベイズ最適化などが使えるのではないかと考えているのですが、ベイズ最適化の仕組みを理解できていないので今後勉強して試してみたいと思っています。
ベイズ最適化:https://www.slideshare.net/hoxo_m/ss-77421091
参考
https://deap.readthedocs.io/en/master/index.html
https://qiita.com/neka-nat@github/items/0cb8955bd85027d58c8e
https://qiita.com/simanezumi1989/items/4f821de2b77850fcf508
Cによる探索プログラミング―基礎から遺伝的アルゴリズムまで 伊庭 斉志
