はじめに
前回遺伝的アルゴリズムでナップザック問題を解いたときに,ブロック崩しを攻略する人工知能には実数値遺伝的アルゴリズムがいいのではないかというコメントをいただいた。よって今回は実数値遺伝的アルゴリズムの勉強をする。
具体的にはNANDゲートを教師データとするニューラルネットワークの最適化である。
また,世代交代モデルにMGG,交叉にBLX-αを使う。
実数値遺伝的アルゴリズム
遺伝的アルゴリズムの遺伝子が実数値である場合を実数値遺伝的アルゴリズムと呼ぶ。
流れは遺伝的アルゴリズムと同じだが,交叉はBLX-αという実数特有の手法がよく使われる。
※ 0,1も実数ですが気にしないでください
※ 遺伝子や染色体についての説明はここにあります
BLX-α(ブレンド交叉)
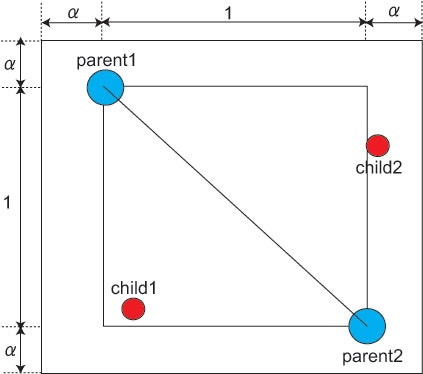
説明がややこしいので遺伝子数を2とする。
親個体を頂点とする正方形を少し大きくした正方形内の領域で,ランダムに子供を作る。
例:下図について,$parent1=[1, 4],parent1=[2, 3]$とすると,$child1$の1番目の遺伝子は 区間 $[1 - α(2 - 1), 2 + α(2 - 1)]$ からランダムに選ばれる。また2番目の遺伝子は 区間 $[3 - α(4 - 3), 4 + α(4 - 3)]$ からランダムに選ばれる。
実装では
//p[0]:親0の遺伝子番号cの遺伝子,p[1]:親1の遺伝子番号cの遺伝子,
var minP = Math.min(p[0],p[1])-ALPHA*Math.abs(p[0]-p[1])
var maxP = Math.max(p[0],p[1])+ALPHA*Math.abs(p[0]-p[1])
child[x][c] = minP + Math.random()*(maxP - minP);
としている。
世代交代モデル
MGG(Minimal Generation Gap)
1.親2個体を個体群からランダム抜きとる
2.親から子をn個体作る
3.親と子を含めた2+n個体から一番評価の高い個体を選ぶ
4.親と子を含めた2+n個体からルーレット選択で1個体選ぶ
5. 3,4の個体を親個体が入っていた個体群に入れる
※ ルーレット選択の実装は前回の記事にある
実装コード
ニューラルネットワーク:3,4,1
個体数:10
世代数:300
交叉率:80%
BLX-α:α=0.5
子の数:20
※ BLX-αのランダム性から突然変異を実装しなくてもいいという資料もあったので,今回突然変異は実装しない
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<title>実数値遺伝的アルゴリズム - ニューラルネットワーク - NANDゲート</title>
</head>
<body>
<script>
(function(){
//遺伝的アルゴリズム
//初期設定
// バイアスありの(3,4,1)ニューラルネットワーク
const INLEN = 3;
const HIDLEN = 4;
const OUTLEN = 1;
var TEST = [[0,0],[0,1],[1,0],[1,1]];//訓練データ
var X = 10;//個体数
var individual = new Array(X);
var chrom = INLEN*(HIDLEN - 1) + HIDLEN*OUTLEN;//遺伝子数=重みの数
//初期の遺伝子決定(ランダム)
for(var x=0;x<X;x++){
individual[x] = new Array(chrom);
for(var c=0;c<chrom;c++){
individual[x][c] = Math.random()-0.5;//-0.5〜0.5
};
};
//操作をGENERATION回繰り返す
const GENERATION = 300;
for(var g=0;g<GENERATION;g++){
if (g == GENERATION-1){
//結果の出力
var best = [E(individual,0),0];
for(var x=0;x<X;x++){
if(E(individual,x)<best[0]){
best[0] = E(individual,x);
best[1] = x;
};
console.log(net(individual,x,TEST[0][0],TEST[0][1]),
net(individual,x,TEST[1][0],TEST[1][1]),
net(individual,x,TEST[2][0],TEST[2][1]),
net(individual,x,TEST[3][0],TEST[3][1]));
};
console.log("best : ", net(individual,best[1],TEST[0][0],TEST[0][1]),
net(individual,best[1],TEST[1][0],TEST[1][1]),
net(individual,best[1],TEST[2][0],TEST[2][1]),
net(individual,best[1],TEST[3][0],TEST[3][1]));
break;
};
//選択と交叉
//MGG選択
const crossrate = 0.8;
if(crossrate>Math.random()){
//親選択
var r1 = Math.floor(Math.random()*X);
var r2 = Math.floor(Math.random()*X);
//親と子供を含めて,エリート+ルーレットで二個体を生成
const CHILDLEN = 22;
var child = new Array(CHILDLEN);
for(var x=0;x<CHILDLEN;x++){
child[x] = new Array(chrom);
for(var c=0;c<chrom;c++){
var p=[individual[r1][c],individual[r2][c]];
if(x==0){
child[0][c] = p[0];
}else if(x==1){
child[1][c] = p[1];
}else{
//BLX-α
const ALPHA = 0.5;
var minP = Math.min(p[0],p[1])-ALPHA*Math.abs(p[0]-p[1])
var maxP = Math.max(p[0],p[1])+ALPHA*Math.abs(p[0]-p[1])
child[x][c] = minP + Math.random()*(maxP - minP);
};
};
};
//誤差関数Eが最小の個体番号の取得
var top = [E(child,0),0]
for(var x=1;x<CHILDLEN;x++){
if(E(child,x)<top[0]){
top[0] = E(child,x);
top[1] = x;
};
};
//ルーレット選択で決定した個体番号の取得
var total = 0;
for(var x=0;x<CHILDLEN;x++){
total += 1.0/E(child,x);
};
var arrow = Math.random()*total;
var select = 0;
for(var x=0,sum=0.0;x<CHILDLEN;x++){
sum += 1.0/E(child,x);
if(sum>arrow){
select = x;
break;
};
};
//疑問:javascriptの配列の特性でindividualが変更されればchildも変更されるのか?
for(var c=0;c<chrom;c++){
individual[r1][c] = child[top[1]][c];
individual[r2][c] = child[select][c];
};
};
//突然変異は行わない
};
//誤差関数E(個体,x:個体番号)
function E(I,x){
var TEACH = [1,1,1,0];
var error = 0.0;
for(var i=0;i<4;i++){
error += Math.pow(TEACH[i]-net(I,x,TEST[i][0],TEST[i][1]),2);
};
return error
};
//シグモイド関数
function sigmoid(x){
const A = 1.0;
return 1.0/(1.0 + Math.exp(-A*x));
};
//ニューラルネットワーク(個体,個体番号,入力0,入力1)
function net(I,x,i0,i1){
var c = 0;
//重み
var input_W = new Array(INLEN);
for(var i=0;i<INLEN;i++){
input_W[i] = new Array(HIDLEN-1);
for(var j=0;j<HIDLEN-1;j++){
input_W[i][j] = I[x][c];
c++;
};
};
var hidden_W = new Array(HIDLEN);
for(var i=0;i<HIDLEN;i++){
hidden_W[i] = new Array(OUTLEN);
for(var j=0;j<OUTLEN;j++){
hidden_W[i][j] = I[x][c];
c++
};
};
//ニューロンの決定
var input_N = [i0,i1,-1];
var hidden_N = new Array(HIDLEN-1);
hidden_N.push(-1);
var output_N = new Array(OUTLEN);
for(i=0;i<HIDLEN-1;i++){
var input_SUM = 0.0;
for(var j=0;j<INLEN;j++){
input_SUM += input_W[j][i]*input_N[j];
};
hidden_N[i] = sigmoid(input_SUM);
};
for(var i=0;i<OUTLEN;i++){
var hidden_SUM = 0.0;
for(var j=0;j<HIDLEN;j++){
hidden_SUM += hidden_W[j][i]*hidden_N[j];
};
output_N[i] = sigmoid(hidden_SUM);
};
return output_N[0];
};
})();
</script>
</body>
</html>
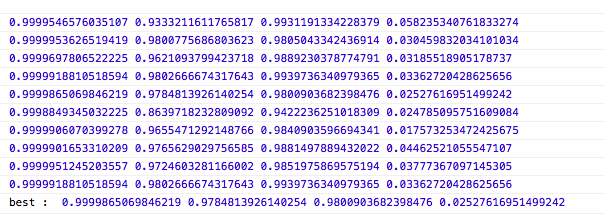
結果
まとめやら,感想やら
遺伝子に実数が扱えたことで,扱いやすくなった気がする。突然変異の実装は,重みの最大最小がわからないと難しそう。私たちのブロック崩し攻略人工知能は,ニューラルネットワークを使っているので,その重みを実数値遺伝的アルゴリズムで最適化していこうと思う。
参考文献
・一番参考にしたサイト
卒論・修論作成のための基礎シリーズ 遺伝的アルゴリズム
Library of Algorithms:視覚的にアルゴリズムを理解するサイト
・MGGの話など
実数値パラメータ最適化のための遺伝的アルゴリズムについて
・BLX-αの図がわかりやすかった。
BLX-αの実装と数値実験
実数値遺伝的アルゴリズムにおける計算モデルの検討
・BLX-αの実装方法
自己組織化マップを再生に用いた遺伝的アルゴリズムに関する研究