点と円の中心を通る直線に平行な円の接線の方程式を求める

点と円の中心を通る直線に平行な円の接線の方程式を求める

点 $Q(x_1,y_1)$ から 中心が $C(x_0,y_0)$ 半径が $r$ の円 $(x-x_0)^2+(y-y_0)^2=r^2$ の中心を結んだ直線に、平行な円の接線の方程式を求める。

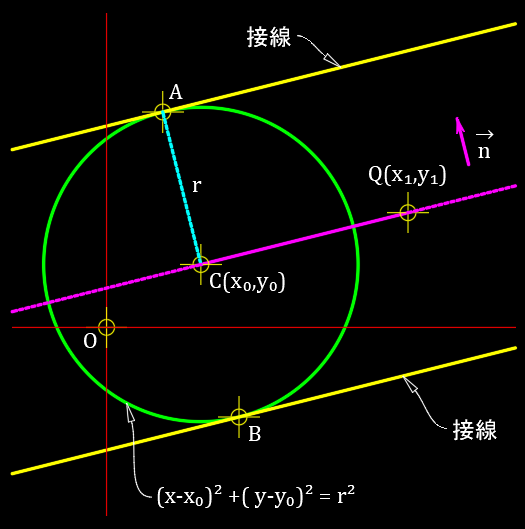
点 $Q(x_1,y_1)$ と円の中心 $C(x_0,y_0)$ を結ぶ直線の方程式は、
$$(y_1-y_0)x+(x_0-x_1)y+(x_1y_0-x_0y_1)=0 \ \cdots \ ①$$

点 $Q$ と円の中心 $C$ を結ぶ直線の方程式を、
$$ax+by+c=0 \ \cdots \ ①$$
とすると、この直線の法線ベクトルは、①により、
$$\vec{n}=(a,b)$$

接線の接点を $A,B$ とすると、
接点 $A$ は、円の中心 $(x_0,y_0)$ から直線の法線ベクトル $\vec{n}$ 方向に 距離 $r$ の点となる。
接点 $B$ は、円の中心 $(x_0,y_0)$ から直線の法線ベクトル $\vec{n}$ 方向に 距離 $-r$ の点となる。

$\vec{n}$ の単位ベクトルを $\vec{h}$ とすると、
$$\vec{h}=\vec{n}\cdot\frac{1}{\sqrt{a^2+b^2}}=(a,b)\cdot\frac{1}{\sqrt{a^2+b^2}}=\left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right)$$
となり接点 $A,B$ の座標は、
$$A=(x_0,y_0)+\left(\frac{a}{\sqrt{a^2+b^2}}\cdot r,\frac{b}{\sqrt{a^2+b^2}}\cdot r\right)=\left(\frac{ar}{\sqrt{a^2+b^2}}+x_0,\frac{br}{\sqrt{a^2+b^2}}+y_0\right)$$
$$B=(x_0,y_0)+\left(\frac{a}{\sqrt{a^2+b^2}}\cdot -r,\frac{b}{\sqrt{a^2+b^2}}\cdot -r\right)=\left(-\frac{ar}{\sqrt{a^2+b^2}}+x_0,-\frac{br}{\sqrt{a^2+b^2}}+y_0\right)$$
となる。

点 $(x_a,y_a)$ 通り、直線 $ax+by+c=0$ に平行な直線の方程式（平行な直線と垂直な直線 参照）は、
$$a(x-x_a)+b(y-y_a)=0$$
この式を展開して整理すると、
$$ax+by-(ax_a+by_a)=0$$
この式の点 $(x_a,y_a)$ に点 $A$ の座標を代入すると、
$$ax+by-\Biggl\{a\left(\frac{ar}{\sqrt{a^2+b^2}}+x_0\right)+b\left(\frac{br}{\sqrt{a^2+b^2}}+y_0\right)\Biggr\}=0$$
この式を展開して整理すると、
$$ax+by-(ax_0+by_0+r\sqrt{a^2+b^2})=0 \ \cdots \ ②$$
ここで、点 $C,Q$ の座標はそれぞれ $(x_0,y_0),(x_1,y_1)$ なので、点 $C,Q$ を結ぶ直線 $ax+by+c=0$ の方程式は、2点を通る直線の方程式の公式により、（直線の方程式 参照）
$$(y_1-y_0)x+(x_0-x_1)y+(x_1y_0-x_0y_1)=0$$
となる。したがって①の式の係数 $a,b,c$ は
$$a=y_1-y_0,\ \ \ \ b=x_0-x_1,\ \ \ \ c=x_1y_0-x_0y_1$$
で、この値を②の式に代入すると、
$$(y_1-y_0)x+(x_0-x_1)y-\Biggr\{(y_1-y_0)x_0+(x_0-x_1)y_0+r\sqrt{(y_1-y_0)^2+(x_0-x_1)^2}\Biggr\}=0$$
整理すると、
$$(y_1-y_0)x+(x_0-x_1)y-(x_0y_1-x_1y_0+r\sqrt{(y_1-y_0)^2+(x_0-x_1)^2})=0$$
これが接点 $A$ 側の接線の方程式です。
同様に接点 $B$ 側を計算すると、
$$(y_1-y_0)x+(x_0-x_1)y-(x_0y_1-x_1y_0-r\sqrt{(y_1-y_0)^2+(x_0-x_1)^2})=0$$
になる。

【例】点 (15,5)と中心(3,2) 半径 5 の円の中心を結んだ直線に平行な円の接線の方程式を求める。

上記公式、
$$(y_1-y_0)x+(x_0-x_1)y-(x_0y_1-x_1y_0+r\sqrt{(y_1-y_0)^2+(x_0-x_1)^2})=0$$
$$(y_1-y_0)x+(x_0-x_1)y-(x_0y_1-x_1y_0-r\sqrt{(y_1-y_0)^2+(x_0-x_1)^2})=0$$
により、1つ目の接線の方程式は、
$$(5-2)x+(3-15)y-(3\cdot5-15\cdot2+5\sqrt{(5-2)^2+(3-15)^2})=0$$
したがって、
$$3x-12y+15-15\sqrt{17}=0$$
小数で表すと、
$$3x-12y-46.8466=0$$
2つ目の接線の方程式は、
$$(5-2)x+(3-15)y-(3\cdot5-15\cdot2-5\sqrt{(5-2)^2+(3-15)^2})=0$$
したがって、
$$3x-12y+15+15\sqrt{17}=0$$
小数で表すと、
$$3x-12y+76.8466=0$$
となる。

サンプルプログラム

円図形を選択して、その次に点を指示。その点と円の中心を通る直線に平行な円の接線を作成する。

;; 点と円の中心を通る直線に平行な円の接線の方程式を求める
(defun c:CreateTangentOfParallelPoint (/ circle point)
    ;; 円を選択
    (while (null circle)
        (setvar 'ERRNO 0)
        (setq circle (car (entsel "円を選択: ")))
        (cond
            ;; 空振り
            ((= 7 (getvar 'ERRNO))
             (princ "\n**空振り!!再選択**\n")
             (setq circle nil)
            )
            ;; 空Enter
            ((= 52 (getvar 'ERRNO))
             (princ "\n**空Enter!!再選択**\n")
             (setq circle nil)
            )
            ;; 図形が選択された
            (circle
             (if (/= "CIRCLE" (entity:GetType circle))
                 (progn
                     (princ "\n**円ではありません!!再選択**\n")
                     (setq circle nil)
                 )
                 (princ "\n**円が選択されました。**\n")
             )
            )
        )
    )
    ;; 点を選択
    (setq point (getpoint "点を指示: " ))

    ;; 接線を作成
    (mapcar
        (function
            (lambda (f)
                (entmake:XlineFromEquation (car f) (cadr f) (caddr f))
            )
        )
        (circle:GetEquationOfParallelPoint circle point)
    )
)

;; == sub functions ==
;; 図形のDXF定義データの値を取得
(defun entity:GetDxf (g e)
    (cond
        ((= (type e) 'ENAME) (cdr (assoc g (entget e))))
        ((listp e) (cdr (assoc g e))) 
    )
)
;; 図形のタイプを取得
(defun entity:GetType (e) (entity:GetDxf 0 e))
;; 円の中心を取得
(defun circle:GetCenterPoint (e) (entity:GetDxf 10 e))
;; 円の半径を取得
(defun circle:GetRadius (e) (entity:GetDxf 40 e))
;; 点と円の中心を通る直線に平行な円の接線の方程式を求める
(defun circle:GetEquationOfParallelPoint (circle point / a b c d r o x0 x1 y0 y1)
    (setq r (circle:GetRadius circle)
          o (circle:GetCenterPoint circle)
          x0 (car o) y0 (cadr o)
          x1 (car point) y1 (cadr point)
          a (- y1 y0) b (- x0 x1)
          c (- (* x0 y1) (* x1 y0))
          d (sqrt (+ (* a a) (* b b)))
    )
    (list
        (list a b (- (- c) (* r d)))
        (list a b (+ (- c) (* r d)))
    )
)

;; 構築線を定義
(defun entmake:XlineBase (p u)
    (list '(000 . "XLINE")
          '(100 . "AcDbEntity")
          '(100 . "AcDbXline")
          (cons 010 p)
          (cons 011 u)
    )
)

;; 基点と単位方向ベクトルから構築線を作成
(defun entmake:Xline (p u) (entmake (entmake:XlineBase p u)) (entlast))

;; 直線の方程式から構築線を作成
(defun entmake:XlineFromEquation (a b c)
    (entmake:Xline (list (- (/ c a)) 0. 0.) (list (- b) a 0.))
)