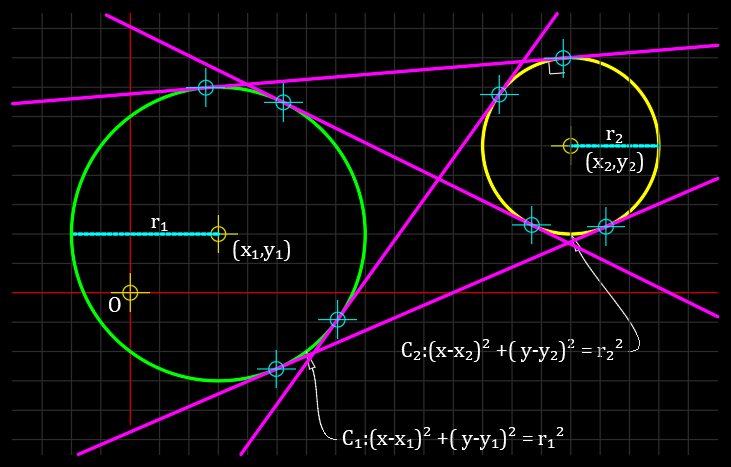
2つの円の位置関係と接線の関係
2つの円の位置関係が
- 離れている場合 ・・・ 接線は4本
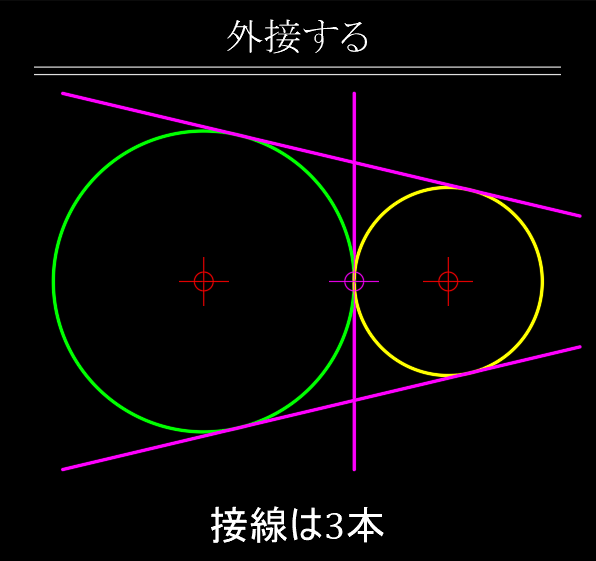
- 外接する場合 ・・・ 接線は3本
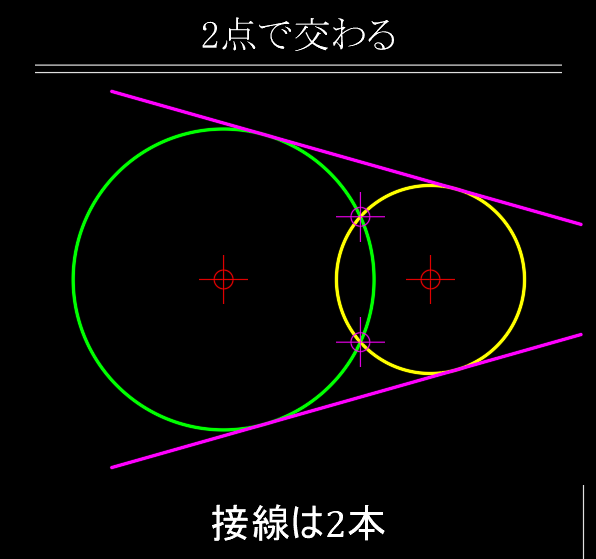
- 2点で交わる場合 ・・・ 接線は2本
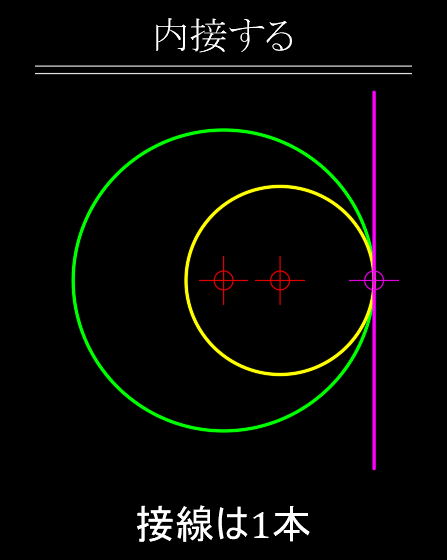
- 内接する場合 ・・・ 接線は2本
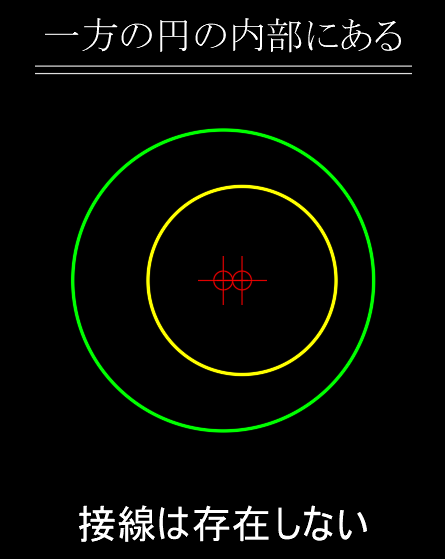
- 一方の円の内部にある場合 ・・・ 接線は存在しない
2つの円の位置関係の判定方法は、2つの円の交点を求める参照
2つの円の位置関係が離れている場合の、4本の共通接線を求める
中心が $(x_1,y_1)$ 半径が $r_1$ の円、 $C_1:(x-x_1)^2+(y-y_1)^2=r_1^2$ と
中心が $(x_2,y_2)$ 半径が $r_2$ の円、 $C_2:(x-x_2)^2+(y-y_2)^2=r_1^2$ の
4本の共通接線を求める。
2つの円 $C_1$ と $C_1$ の位置関係は離れているものとする。
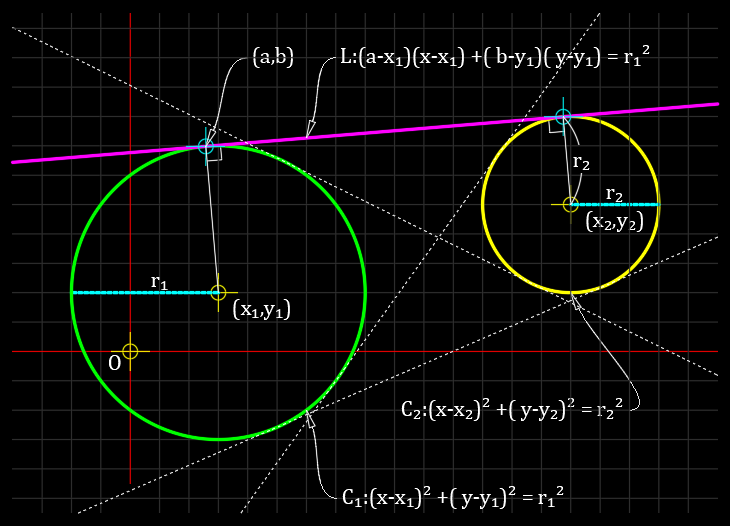
円 $C_1$ 上の点 $(a,b)$ が求める接線の接点である場合、その接線の方程式は、(点から円への接点を求める 参照)
$$L:(a-x_1)(x-x_1)+(b-y_1)(y-y_1)=r_1^2$$
となる。また、
この接線 $L$ が円 $C_2$ の接線でもあるための条件は、
$L$ と $C_2$ の中心 $(x_2,y_2)$ との距離が、$C_2$ の半径 $r_2$ である必要がある。
接線 $L$ の方程式を展開して、直線の方程式一般形の形に変形すると、
$$(a-x_1)x+(b-y_1)y-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)=0$$
となり、接線 $L$ と $(x_2,y_2)$ との距離は、点と直線の距離の公式により、
$$\frac{\mid (a-x_1)x_2+(b-y_1)y_2-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)\mid}{\sqrt{(a-x_1)^2+(b-y_1)^2}}$$
で、これが半径 $r_2$ と同じである必要があるので、
$$\frac{\mid (a-x_1)x_2+(b-y_1)y_2-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)\mid}{\sqrt{(a-x_1)^2+(b-y_1)^2}}=r_2 \ \cdots \ ①$$
となる。
また、点 $(a,b)$ は円 $C_1$ 上の点なので、
$$(a-x_1)^2+(b-y_1)^2=r_1^2\ \cdots \ ②$$
が成り立つ。よって、
$$\sqrt{(a-x_1)^2+(b-y_1)^2}=r_1$$
この式の左辺は、①の式の左辺の分母と同じなので、①の式は、
$$\frac{\mid (a-x_1)x_2+(b-y_1)y_2-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)\mid}{r_1}=r_2$$
すなわち、
$$\mid (a-x_1)x_2+(b-y_1)y_2-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)\mid=r_1r_2\ \cdots \ ③$$
となる。
③の式は、左辺が絶対値になっているので、
$$(a-x_1)x_2+(b-y_1)y_2-(x_1(a-x_1)+y_1(b-y_1)+r_1^2)=r_1r_2\ \cdots \ ④$$
$$(a'-x_1)x_2+(b'-y_1)y_2-(x_1(a'-x_1)+y_1(b'-y_1)+r_1^2)=-r_1r_2\ \cdots \ ④'$$
の2つの意味がある。
まず $②$ と $④$ の式を使って、接点 $(a,b)$ を求める。
計算式を単純にするために、$a-x_1=A, b-y_1=B$とおくと
$②$ の式は
$$A^2+B^2=r_1^2$$
変形して、
$$A^2+B^2-r_1^2=0\ \cdots \ ⑤$$
$④$ の式は
$$x_2A+y_2B-x_1A-y_1B-r_1^2=r_1r_2\ \dashrightarrow \ (x_2-x_1)A+(y_2-y_1)B=(r_1+r_2)r_1$$
となりさらに、$x_2-x_1=X, y_2-y_1=Y, r_1+r_2=R$とおくと
$$XA+YB=Rr_1$$
この式を $B$ について解くと、
$$B=\frac{Rr_1-XA}{Y}$$
この $B$ の値を ⑤に代入すると、
$$A^2+\left(\frac{Rr_1-XA}{Y}\right)^2-r_1^2=0\ \dashrightarrow \ A^2+\frac{(Rr_1-XA)^2}{Y^2}-r_1^2=0$$
両辺に $Y^2$ を掛ける、
$$Y^2A^2+(Rr_1-XA)^2-Y^2r_1^2=0$$
この式を展開して、
$$Y^2A^2+R^2r_1^2-2Rr_1XA+X^2A^2-Y^2r_1^2=0$$
整理すると、
$$(X^2+Y^2)A^2-2XRr_1A+r_1^2(R^2-Y^2)=0\ \cdots \ ⑥$$
となる。この式の $A$ を2次方程式の解の公式を使って解く。
2次方程式 $ax^2+bx+c=0$ の解の公式は、
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
⑥の式で解の公式の係数 $a,b,c$ に相当する値は、
$a=X^2+Y^2$
$b=-2XRr_1$
$c=r_1^2(R^2-Y^2)$
で、この値を解の公式に代入すると、
$$A=\frac{2XRr_1\pm\sqrt{(-2XRr_1)^2-4r_1^2(X^2+Y^2)(R^2-Y^2)}}{2(X^2+Y^2)}$$
$(-2XRr_1)^2$ を展開して、
$$A=\frac{2XRr_1\pm\sqrt{4X^2R^2r_1^2-4r_1^2(X^2+Y^2)(R^2-Y^2)}}{2(X^2+Y^2)}$$
平方根のなかを $4r_1^2$ でくくる、
$$A=\frac{2XRr_1\pm\sqrt{4r_1^2(X^2R^2-(X^2+Y^2)(R^2-Y^2))}}{2(X^2+Y^2)}$$
$-(X^2+Y^2)(R^2-Y^2)$ を展開、
$$A=\frac{2XRr_1\pm\sqrt{4r_1^2(X^2R^2-X^2R^2+X^2Y^2-Y^2R^2+Y^4)}}{2(X^2+Y^2)}$$
$X^2R^2$ が消えて、さらに $4Y^2r_1^2$ でくくる
$$A=\frac{2XRr_1\pm\sqrt{4Y^2r_1^2(X^2+Y^2-R^2)}}{2(X^2+Y^2)}$$
$4Y^2r_1^2$ を平方根の外に出す
$$A=\frac{2XRr_1\pm2Yr_1\sqrt{X^2+Y^2-R^2}}{2(X^2+Y^2)}$$
約分すると
$$A=\frac{XRr_1\pm Yr_1\sqrt{X^2+Y^2-R^2}}{X^2+Y^2}$$
となり、この式の $A,X,Y,R$ を元の値に戻すと、
$$a-x_1=\frac{(x_2-x_1)(r_1+r_2)r_1\pm (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-x_1)^2+(y_2-y_1)^2}$$
したがって、$$a=\frac{(x_2-x_1)(r_1+r_2)r_1\pm (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-x_1)^2+(y_2-y_1)^2}+x_1$$
これが、接点の $x$ 座標の値 $a$ を求める公式です。
同じ方法で $b$ を求めると(式は省略)
$$b=\frac{(y_2-y_1)(r_1+r_2)r_1\mp (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-x_1)^2+(y_2-y_1)^2}+y_1$$
となる。
さらに同じ要領で $②$ と $④'$ の式を使って、接点 $(a',b')$ を求めると、(式は省略)
$$a'=\frac{(x_2-x_1)(r_1-r_2)r_1\pm (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-x_1)^2+(y_2-y_1)^2}+x_1$$
$$b'=\frac{(y_2-y_1)(r_1-r_2)r_1\mp (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-x_1)^2+(y_2-y_1)^2}+y_1$$
となる。
これで、円 $C_1$ の4つの接線の接点の座標を求めることができ、
この4つの接点における、円 $C_1$ の接線の方程式が、円 $C_1$ と $C_2$ の4本の共通接線となる。
整理すると、
円 $C_1$ と $C_2$ の4本の共通接線を $L_1,L_2,L_3,L_4,$
その各接線の円 $C_1$ の4つの接点の座標を $(a_1,b_1), (a_2,b_2), (a_3,b_3), (a_4,b_4)$ とすると、
接点の座標は、
$$\begin{cases}
a_1=\dfrac{(x_2-x_1)(r_1+r_2)r_1 + (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+x_1 \\
b_1=\dfrac{(y_2-y_1)(r_1+r_2)r_1 - (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+y_1
\end{cases}$$
$$\begin{cases}
a_2=\dfrac{(x_2-x_1)(r_1+r_2)r_1 - (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+x_1 \\
b_2=\dfrac{(y_2-y_1)(r_1+r_2)r_1 + (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1+r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+y_1
\end{cases}$$
$$\begin{cases}
a_3=\dfrac{(x_2-x_1)(r_1-r_2)r_1 + (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+x_1 \
b_3=\dfrac{(y_2-y_1)(r_1-r_2)r_1 - (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+y_1
\end{cases}$$
$$\begin{cases}
a_4=\dfrac{(x_2-x_1)(r_1-r_2)r_1 - (y_2-y_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+x_1 \
b_4=\dfrac{(y_2-y_1)(r_1-r_2)r_1 + (x_2-x_1)r_1\sqrt{(x_2-x_1)^2+(y_2-y_1)^2-(r_1-r_2)^2}}{(x_2-
x_1)^2+(y_2-y_1)^2}+y_1
\end{cases}$$
で、接線の方程式は、
$$L_1:(a_1-x_1)(x-x_1)+(b_1-y_1)(y-y_1)=r_1^2$$
$$L_2:(a_2-x_1)(x-x_1)+(b_2-y_1)(y-y_1)=r_1^2$$
$$L_3:(a_3-x_1)(x-x_1)+(b_3-y_1)(y-y_1)=r_1^2$$
$$L_4:(a_4-x_1)(x-x_1)+(b_4-y_1)(y-y_1)=r_1^2$$
となる。
サンプルプログラム
2つ円図形を選択して、共通接線を作成する。
;; 2つの円の共通接線を作成する
(defun c:CreateCommonTangent (/ c1 c2)
(setq c1 (editor:EntselCircle "1つ目の円を選択")
c2 (editor:EntselCircle "2つ目の円を選択")
)
;; 共通接線を作成する
(mapcar
(function
(lambda (x)
(entmake:XlineFromEquation (car x) (cadr x) (caddr x))
)
)
(circle:GetCommonTangent c1 c2)
)
)
Subfunctions
;; == Subfunctions ==
;; 図形のDXF定義データの値を取得
(defun entity:GetDxf (g e)
(cond
((= (type e) 'ENAME) (cdr (assoc g (entget e))))
((listp e) (cdr (assoc g e)))
)
)
;; 図形のタイプを取得
(defun entity:GetType (e) (entity:GetDxf 0 e))
;; 円図形をentsel 選択
(defun editor:EntselCircle (msg / circle)
;; 円を選択
(while (null circle)
(setvar 'ERRNO 0)
(setq circle (car (entsel (strcat "\n" msg " :\n"))))
(cond
;; 空振り
((= 7 (getvar 'ERRNO))
(princ "\n... 空振り! 再選択 ...\n")
(setq circle nil)
)
;; 空Enter
((= 52 (getvar 'ERRNO))
(princ "\n... 空Enter! 再選択 ...\n")
(setq circle nil)
)
;; 図形が選択された
(circle
(if (/= "CIRCLE" (entity:GetType circle))
(progn
(princ "\n... 円ではありません! 再選択 ...\n")
(setq circle nil)
)
(princ "\n... 円が選択されました。\n")
)
)
)
)
circle
)
;; 円周上の点を通る円の接線の方程式を求める
(defun circle:GetTangent(circle point / r o a b p q)
(setq r (circle:GetRadius circle1)
o (circle:GetCenterPoint circle1)
a (- (car point) (setq p (car o)))
b (- (cadr point) (setq q (cadr o)))
)
(list a b (- (+ (* p a) (* q b) (* r r))))
)
;; 2つの円の共通接線を求める
(defun circle:GetCommonTangent (circle1 circle2
/ r1 r2 o1 o2 x1 x2 y1 y2 X Y R+ R- W Z1 Z2 a1 a2 a3 a4 b1 b2 b3 b4)
(setq r1 (circle:GetRadius circle1)
o1 (circle:GetCenterPoint circle1)
x1 (car o1)
y1 (cadr o1)
)
(setq r2 (circle:GetRadius circle2)
o2 (circle:GetCenterPoint circle2)
x2 (car o2)
y2 (cadr o2)
)
(setq X (- x2 x1) Y (- y2 y1)
R+ (+ r1 r2) R- (- r1 r2)
)
(setq W (+ (* X X) (* Y Y))
Z1 (sqrt (- W (* R+ R+)))
Z2 (sqrt (- W (* R- R-)))
)
(setq a1 (+ (/ (+ (* X R+ r1) (* Y r1 Z1)) W) x1)
b1 (+ (/ (- (* Y R+ r1) (* X r1 Z1)) W) y1)
a2 (+ (/ (- (* X R+ r1) (* Y r1 Z1)) W) x1)
b2 (+ (/ (+ (* Y R+ r1) (* X r1 Z1)) W) y1)
a3 (+ (/ (+ (* X R- r1) (* Y r1 Z2)) W) x1)
b3 (+ (/ (- (* Y R- r1) (* X r1 Z2)) W) y1)
a4 (+ (/ (- (* X R- r1) (* Y r1 Z2)) W) x1)
b4 (+ (/ (+ (* Y R- r1) (* X r1 Z2)) W) y1)
)
(list
(circle:GetTangent circle1 (list a1 b1))
(circle:GetTangent circle1 (list a2 b2))
(circle:GetTangent circle1 (list a3 b3))
(circle:GetTangent circle1 (list a4 b4))
)
)
;; 構築線を定義
(defun entmake:XlineBase (p u)
(list '(000 . "XLINE")
'(100 . "AcDbEntity")
'(100 . "AcDbXline")
(cons 010 p)
(cons 011 u)
)
)
;; 基点と単位方向ベクトルから構築線を作成
(defun entmake:Xline (p u) (entmake (entmake:XlineBase p u)) (entlast))
;; 直線の方程式から構築線を作成
(defun entmake:XlineFromEquation (a b c)
(entmake:Xline (list (- (/ c a)) 0. 0.) (list (- b) a 0.))
)