クラスタリング手法としてのk-means法

輪読がてら書いた記事...
スライドも埋められるらしいのでこれをもうレジュメとして使ってしまうつもり

はじめに

本記事ではクラスタリングにおいて有名な手法であるk-means法を紹介する。本記事はスタンフォード大学のIntroduction to Applied Linear Algebra – Vectors, Matrices, and Least Squaresの第1章4節の内容をもとにしている。日本語版も発売されているので是非とも一読することを勧める。

本記事ではk-means法のコードを扱わない。

クラスタリング

本節では、クラスタリングの基本概念を紹介し、そのタスクを表す式の理解を目指す。

クラスタリングとは？

クラスタリングについて、いま一度確認しておく。
クラスタリングとは、いくつかのベクトル似ているもの同士でいくつかの群に分けることをいう。
たとえば、次の画像を見てほしい。

上図は、$N = 300$である2次元ベクトルを点で表現したものである。この集合は$k = 3$の集合に分割できることが見てわかるだろう。

クラスタリングの定義

先程クラスタリングについて説明したが、このタスクをうまく表現するための要素を紹介する。以下、$i$をデータの添え字、$j$を群に対する添え字とする。$(i \in [1,N], j \in[1,k])$

今、N個のn次元ベクトル$x_1, x_2, ... ,x_N$を考える。
$1,2,...,k$とラベリングされた群のいずれかに割り当てられることを表現するために、n次元ベクトル$c$を用いる。ここで$c_i$は$x_i$が何の群に割り当てられるのかを表現する。

また、$G_j$を群$j$に対応する添字の集合とする。つまり、$G_j = \{i | c_i = j\}$である。
各群に対して代表としてn次元ベクトル$z_1,z_2,...z_k$を関連付ける。代表ベクトルは各群のベクトルに近い、すなわち$||x_i - z_{c_i}||$が最も小さくなるベクトルである。ただし、代表ベクトルは与えられたベクトルのいずれかである必要はない。

クラスタリングの評価を行うために、次の関数を導入する。
$
J^{clust} = (||x_1 - z_{c_1}||^2 + ||x_2 - z_{c_2}||^2 + ... +||x_N - z_{c_N}||^2)/N
$
この関数は、各ベクトルとそれに対応する代表ベクトルとの2乗距離の平均である。これが小さいほど良いグループ分けができていることになる。$J^{clust}$が小さいほど良いクラスタリングができていると評価する。つまり、クラスタリングのタスクというのは$J^{clust}$を最小にできる群割り当て$c_1,...c_N$と代表ベクトル$z_1,...z_k$を求めることと言い換えられる。

クラスタリングのためのアルゴリズム

本節ではクラスタリングを行う上でよく用いられるk-means法の概念と考え方を説明する。

最適解とアルゴリズム　

クラスタリングについて評価できるようになったので、このタスクを解決するアルゴリズムを考えていく。まずは群割り当て又は代表ベクトルのいずれかからもう片方を求める方法について考えてみる。

代表ベクトルから群割り当てを求める

代表ベクトル$z_1,...,z_k$が固定されているとして、$J^{clust}$を最小にできる群の割り当て$c_1,...c_N$を求めることを考える。
とは言っても難しいことはない。$c_i$の選択は$J^{clust}$の$||x_i - z_{c_i}||^2/N$にのみ影響を与える。そのため、$c_i$を$j$について$||x_i - z_j||^2$が最小になるように選択すればよい。これは、あるデータに対して、最も位置が近い代表ベクトルのグループに割り当てるということである。

群割り当てから代表ベクトルを求める

群の割り当て$c_1,...c_N$が固定されているとして、$J^{clust}$を最小にできる代表ベクトル$z_1,...,z_k$を求めることを考える。まず,$J^{clust}$を$k$項の和に並べ替える。
$
J^{clust} = J_1 + ...+J_k
$
各$J$の項に対して、$G$を用いることで以下のように表現できる。
$
J_j = (1/N) \sum_{i\in{G_j}}||x_i - z_j||^2
$
式から、$z_j$は$J^{clust}$の他の項に影響を与えないので、$z_j$は$J_j$のみによる。
$J_j$を最小化する$z_j$は、群$j$に所属するベクトルの重心であることは明らかだろう。式で表現すると以下のようになる。各代表ベクトルは以下の式で求められる。
$
z_j = (1/{|G_j|}) \sum_{i\in{G_j}}x_i
$

k-means法 (k-平均値法)

代表ベクトルから最適な群割り当てを求められることと、群割り当てから最適な代表ベクトルを求めることができることを示した。これらを用いて最適なクラスタリングを行えそうである。しかし、両者は共依存の関係にある。そこで、両者の更新を繰り返し行ってみる手法が考案された。これがk-means法である。

k-means法の手順

目的: 各グループ内のベクトルが互いに近くなるようにデータをグループ化すること
手順:1. k個の代表ベクトルをランダムに決める
以下の手順2~4を収束するまで繰り返す
2. 各データベクトル$x_i$について、||x_i-z_j||^2を最小にするような$j$を選び、そのグループに割り当てる。
3. 各グループ$j$について、新しい代表ベクトル $z_j$を、そのグループに割り当てられたすべてのベクトルの平均（重心）に更新する
4. グループの割り当てが変化しなくなったら終了する

k-means法の強点

このアルゴリズムは、必ずある解に収束することが分かっている。手順2~4が目的関数$j^{clust}$を増加させることはなく、また$J^{clust}$は下に有界であるからだ。下図を見てほしい。

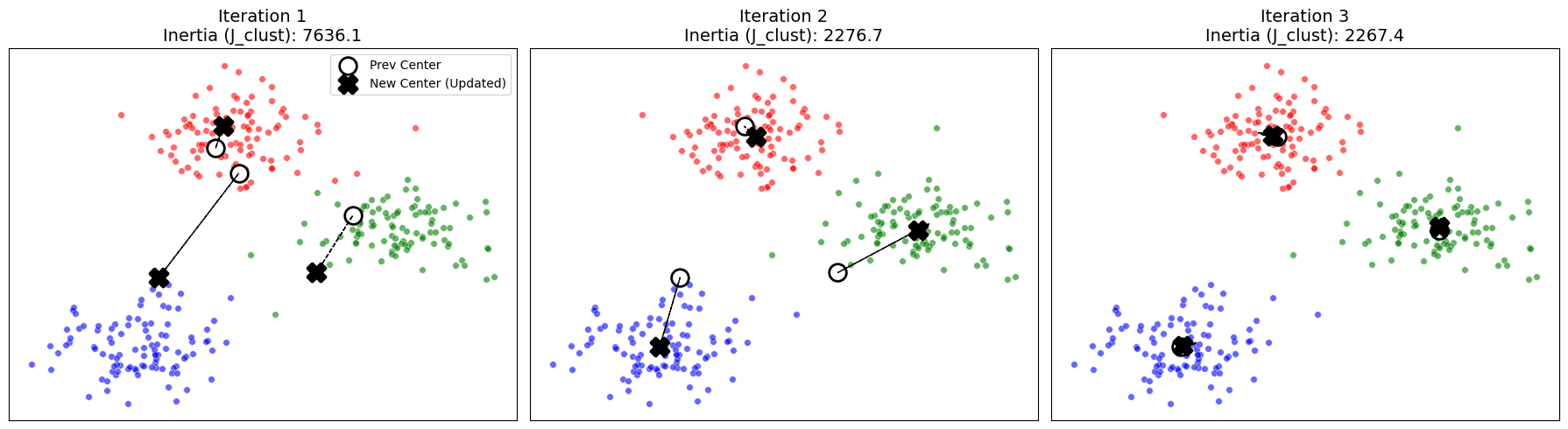
この図を見ると、少しずつ代表ベクトルの移動距離が短くなってきていることがわかるだろう。

また、k-means法は計算効率が良いことで知られている。
たとえば、手順2では各ベクトルに対して各ベクトルの代表ベクトルとの距離を計算するため、計算数は$O(Nkn)$となる。手順3では、ベクトルの平均を計算するため、計算量は$O(Nn)$となる。全体として、1回の反復当たりのオーダーは$Nkn$となる。データ数に対して線形であるから、数億個のデータを扱うような大規模の問題にも適用可能だ。

実のところ、k-means法はヒューリスティックである。初期値が異なれば違う解に収束するので、求めた解が$J^{clust}$を最小化できることを保証できない。そのため、異なる初期値を与えて複数回実行し、求めた解のうち$J^{clust}$を最小にするものを選ぶことが一般的である。

使用例

ここまでは、クラスタリング及びそのアルゴリズムについて紹介した。本節では、それらの利用のされ方を紹介する。

クラスタリングの使用例

トピック発見（文書解析）:

文書を単語の出現頻度（ヒストグラム）に基づいてベクトル化することで同じトピック、ジャンル、あるいは著者の文書をグループ化する。
アルゴリズムは単語の意味を知らずとも、自動的にトピックを発見できるという利点がある。

他にも、

• 顧客の市場セグメンテーション
• 患者のクラスタリング
• 金融セクターの分類
  等が挙げられる。

応用例

k-means法は多くの用途と応用がある。本節ではそれらを紹介する。

欠損値の補填

データの一部（例：ある人の年齢）が欠けている場合、わかっている他の特徴を使ってそのデータが属するクラスタを特定する。そのクラスタの代表ベクトル（平均値）の該当項目（年齢）を、欠損値の推定値として利用することができる。

分類

事前にデータをクラスタリングして各グループにラベル（意味）を付けておき、新しいデータが来た際に、最も近いグループ代表ベクトルを探すことで、そのデータがどのクラスに属するかを自動的に判別する。（例：手書き数字の自動認識）

付録

最後に、本文中で使用した図を作成するために用いたコードを添付しておく。google collab上で実行した。
最近のgeminiは優秀だなと感じたのであった...

図1

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 1. データの生成 (300点, 3つの中心, ばらつきを調整)
# random_stateを変更すると、クラスターの位置形状が変わります
X, y = make_blobs(n_samples=300, centers=3, cluster_std=2.0, random_state=42)

# 2. プロットの準備 (1行2列のサブプロット)
fig, axes = plt.subplots(1, 2, figsize=(14, 6))

# --- 左側の図: 未分類のデータ (全て黒色) ---
axes[0].scatter(X[:, 0], X[:, 1], c='black', s=30, edgecolor='white', linewidth=0.5)
axes[0].set_title("Original Data (Unlabeled)", fontsize=14)
axes[0].set_xticks([]) # 軸目盛りを消して「図」としての純度を高める
axes[0].set_yticks([])

# --- 右側の図: クラスタリング済みデータ (色分け) ---
# 指定された画像に合わせて 赤・緑・青 を割り当て
colors = ['red', 'green', 'blue']

for i in range(3):
    # ラベル i に該当するデータのみを抽出してプロット
    axes[1].scatter(X[y == i, 0], X[y == i, 1], c=colors[i], 
                    label=f'Cluster {i+1}', s=30, edgecolor='white', linewidth=0.5)

axes[1].set_title("Clustered Data", fontsize=14)
axes[1].set_xticks([])
axes[1].set_yticks([])

# レイアウト調整と保存/表示
plt.tight_layout()
plt.show()

図2

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

# 1. データの生成（前回と同様）
X, y_true = make_blobs(n_samples=300, centers=3, cluster_std=2.0, random_state=42)

# 2. 初期重心の決定（再現性のため乱数シードを固定して選択）
# 実際のK-means++などではなく、あえて単純なランダム選択で開始します
np.random.seed(10) # このシードを変えると初期位置が変わります
initial_indices = np.random.choice(X.shape[0], 3, replace=False)
centers = X[initial_indices]

# 3. プロットの準備（横に3つ並べる）
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
colors = ['red', 'green', 'blue']

# 現在の重心を保持する変数
current_centers = centers

# --- 1回目から3回目までの反復を実行して描画 ---
for i in range(3):
    # ax: 現在のサブプロット
    ax = axes[i]

    # K-meansを1ステップだけ実行
    # initに現在の重心を渡し、max_iter=1, n_init=1とすることで1回だけ更新を行います
    kmeans = KMeans(n_clusters=3, init=current_centers, max_iter=1, n_init=1, random_state=42)
    kmeans.fit(X)

    # 結果の取得
    labels = kmeans.labels_                # 各点の所属クラスタラベル
    new_centers = kmeans.cluster_centers_  # 更新後の新しい重心
    inertia = kmeans.inertia_              # 目的関数値 (J_clust)

    # データ点のプロット（所属クラスタで色分け）
    for cluster_idx in range(3):
        ax.scatter(X[labels == cluster_idx, 0], X[labels == cluster_idx, 1],
                   c=colors[cluster_idx], s=30, edgecolor='white', linewidth=0.5, alpha=0.6)

    # 重心（Centroids）の移動をプロット
    # 移動前の重心（白丸に黒枠）
    ax.scatter(current_centers[:, 0], current_centers[:, 1],
               s=200, c='white', edgecolor='black', marker='o', linewidth=2, label='Prev Center')
    # 移動後の重心（大きな×印）
    ax.scatter(new_centers[:, 0], new_centers[:, 1],
               s=200, c='black', marker='X', linewidth=3, label='New Center (Updated)')

    # 重心の移動軌跡を矢印で描画（視覚的補助）
    for j in range(3):
        ax.arrow(current_centers[j, 0], current_centers[j, 1],
                 new_centers[j, 0] - current_centers[j, 0],
                 new_centers[j, 1] - current_centers[j, 1],
                 head_width=0.5, head_length=0.7, fc='black', ec='black', linestyle='--')


    # タイトルと見た目の調整
    # Inertia (J_clust) の値をタイトルに表示して減少を確認できるようにする
    ax.set_title(f"Iteration {i+1}\nInertia (J_clust): {inertia:.1f}", fontsize=14)
    ax.set_xticks([])
    ax.set_yticks([])
    if i == 0:
        ax.legend() # 最初の図にだけ凡例を表示

    # 次のステップのために重心を更新
    current_centers = new_centers

plt.tight_layout()
# 必要に応じて保存コードを追加してください
# plt.savefig('kmeans_iterations.png', dpi=300, bbox_inches='tight')
plt.show()