感染症数理モデルについて

感染症モデルについて

感染症数理モデルである，SISモデルについて質問です．

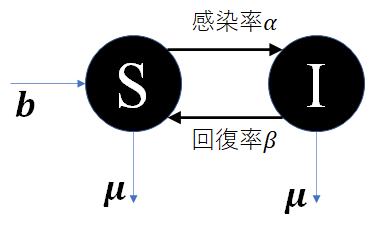
上の図のようなモデルを考えます．
感染率$\alpha$，回復率$\beta$, 誕生率(？)$b$，死亡率$\mu$です．
このようなモデルにおいて，微分方程式を考えると，

\frac{dS(t)}{dt} = b+\beta I(t)-\alpha S(t)I(t) - \mu S(t)\\
\frac{dI(t)}{dt} = -\beta I(t)+\alpha S(t)I(t) - \mu I(t)

となると思います（間違っていたら申し訳ございません）．
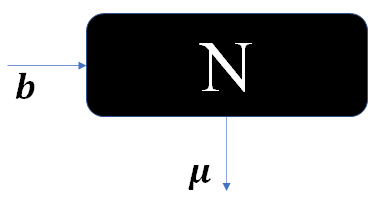
また，時刻$t$における全人口を$N(t)$とすると，$S(t)+I(t)=N(t)$が成り立つとします．

このとき，

　　　　　　　　　　　　　　　　　　$\frac{dN(t)}{dt}=b-\mu N(t)$　　　　(1)

となり，

　　　　　　　　　　　　　　　　　　$\lim_{t\to\infty}N(t)=\frac{b}{\mu}$　　　　(2)

となる，というのをどこかで見た（記憶があいまい）のですが，それはなぜですか？

(1)式は，

こんな感じで考えれば式を立てれるんですが，(2)式は，直感的には理解できますが，数学的な説明がわかりません．
(1)の式を書き換えて(2)式を説明したりできるのでしょうか，，，

的外れな質問でしたら申し訳ございません．
数学初心者ですがよろしくお願いします．