はじめに
ひつじ橋です🐑
今回は,
SVM(サポートベクターマシン)を扱います.
「教師あり学習」のできるアルゴリズムです.
SVMとは?
・・・ Support Vector Machineの略.
Support Vector とは, 「データを分割する直線に最も近いデータ点」のことです.
SVを定める
➡️ データの分割線が決まる
➡️ この線よりも上か下か, で属するクラスを予測できる
というように用います.
SVMでは, このSVがカギです🔑
イメージ
いま, 平面上の点をピンクのグループと青のグループとに分けたい!とします.
これらを分けるのに, 最も適した分割線はどちらでしょうか??
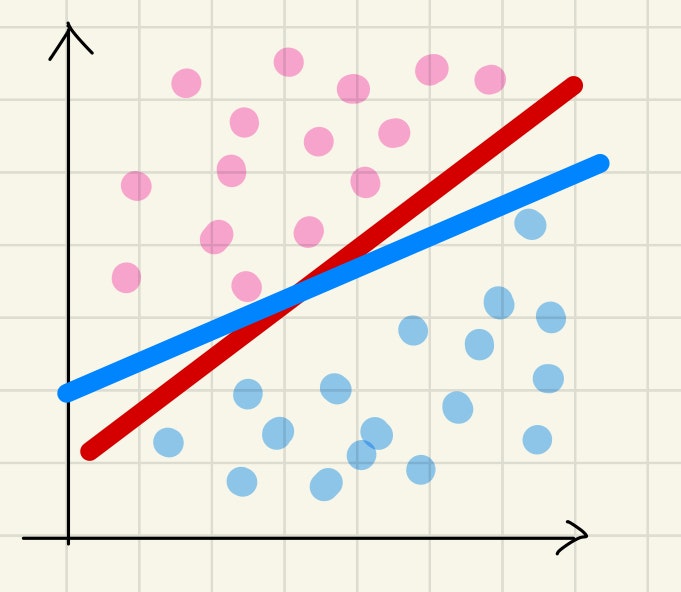
この判断を理論的に行うのが, SVMです.
①SVMの強み
1. 識別精度が落ちにくい
データの次元が大きくなっても識別精度を保てるのがメリットの一つです.
2. 過学習を起こしづらい
少ない教師データで高い汎化性(未知のテストデータに対する識別の性能)を持つため、過学習が起こりにくくなります.
②SVMの弱み
1. 学習データが増えると計算量が膨大に
偏りやばらつきが見られる非線形データの場合は特に, 膨大な計算量になってしまいます.
2. スケーリングが必要になる
前処理として, スケーリング(複数の異なる特徴量を, ある基準で変換し, 尺度を統一すること)が必要です.
これをしないと, 誤差が生じるリスクが高まります.
③活用できる場面
SVMは, 2分類の線形識別を得意とするため,
主に二者択一の予測に用いられます.
たとえば, スパムメールの検出に用いられます.
この場合, 「スパムメール」と「通常のメール」が区別すべきクラスになります.
別の例として, 株価の予測も挙げられます.
ここでも, 前日より「株価が上がるか」, 「株価が下がるか」の2つに分類されます.
(参考)
SVMの手法
次に,SVMの手法を見ていきます.
この過程で考えるべきことは, 主に2つあります.
①マージンの最大化
②特徴マッピング
①マージンの最大化
WORD
🌟マージン・・・クラスの分類基準となる境界と、各データとの距離のこと.
.
つまり, 「マージンの最大化」とは, SVから最も遠い位置に境界線を引くことを意味します.
仮にマージンが小さいと,
データが少しずれれば境界を越えてしまうため, 誤判定につながりやすくなると予想されます.
マージンの算出
STEP1
あるデータと分割線との距離を得るには, 「点と直線の距離」を求めます.
いま, 座標平面上の任意の点を $(x_0,y_0)$,
考えたい直線の方程式を $ax+by+c = 0$
とします.
ベクトル
w = (a, b)
を用い, さらに直線の方程式の$x$と$y$を$x_0$, $x_1$と書き換えた上で,
x = (x_0, x_1)
とおくと, 「点と直線の距離」は
d = \frac{\left|{(w^T, x) + c}\right|}{\left|w\right|}
で表すことが可能です.
ここで, $(w^T, x)$は$w^T$と$x$の内積です.
注
今後, $c$を$b$と書き換えることにします.
.
.
WORD
🌟重み・・・$w$のこと.
🌟バイアス・・・スカラー定数 $b$のこと.
これらの組み合わせによって, $2$以上の任意の整数次元を取ることができ, まとめて「超平面」と呼びます.
超平面の選び方は自由なので, 重みとバイアスには共に, 定数倍の任意性があります.
STEP2
さて,
m = \min_k\frac{\left|{(w^T, x_k) + b}\right|}{\left|w\right|}
を最大化すればよいわけですが...
先述の通り, $w$と$b$は定数倍を問わないので,
計算しやすいように
m = \frac 1{\left|w\right|}
と標準化しておきます.
すると, 任意の$k=1,2,...,N$($N$は学習データ数)に対し,
\frac{\left|{(w^T, x_k) + b}\right|}{\left|w\right|} \ge m
は
\left|((w^T, x_k)+b)-1\right| \geq 0
と書くことができます.
あとは, この条件下で
m = \frac 1{\left|w\right|}
を最大化するのみです!
が, ここで問題を
\frac {{\left|w\right|}^2}{2}
の最小化, へと読み替えることにします.
STEP3
{t_k= \left\{
\begin{array}{ll}
1 & (x_kがクラス1のとき) \\
-1 & (x_kがクラス2のとき)
\end{array}
\right.
}
と定めると, 条件は
\min_k t_k((w^T,x_k) + b) = 1 \Leftrightarrow t_k((w^T,x_k) + b) \geq 1
と書き換えることができます.
STEP4
あとは, ラグランジュの未定係数法を用いて, 上の条件下での
L(w,b,\alpha)=f(w)-\sum_{k=1}^{N}\alpha_k(t_k((w^T, x_k) + b) - 1)\\
の極値を求めにかかります.
{\frac{\partial L}{\partial w}=0 \quad \Rightarrow \quad w=\sum_{k=1}^{N}\alpha_k t_k x_k\\}
{\frac{\partial L}{\partial b}=0 \quad \Rightarrow \quad \sum_{k=1}^{N}\alpha_k t_k=0
}
これらを$L$に代入すれば,
L(\alpha) = \frac1 2 \sum_{k = 1}^{N} \sum_{l = 1}^{N} \alpha_k \alpha_l t_k t_l ({x_k}^T, x_l) - \sum_{k = 1}^{N} \alpha_k
となります.
さらに, カルーシュ・キューン・タッカー(KKT)条件から,
最終的に
{\sum_{k=1}^{N}\alpha_k y_k=0\\
}
{\alpha_k \geq 0
}
という条件下で$L$を最小化すればよいことになります.
(参考)
②特徴マッピング
さて, 実際には,
「どのような分割線で区切っても, 線形分離ができない」
状況もあります.
そのときは, より高次元の空間に転写して考えます.
「平面上で分割線を描けないなら, 平面で線形分離すればいいじゃない」
というわけです.
カーネルトリック
しかし, 次元が増えれば計算も困難になることが見込まれます...
そこで用いられるのが, カーネル関数を用いたカーネルトリックです.
このカーネル関数の選択基準に関して, 明確なものはないようです.
よく使われるものが, 以下のサイトにまとめられています.
(参考)
おわりに
今回は, 先輩である @Hiroki_Akita 様の記事を参考に, 学習を進めさせていただきました.
ありがとうございました...!