前回の続きです。
アメダスのデータをPythonに取り込むところまでを作ってみました。
今回は回帰分析をニューラルネットワークでやってみようというテーマについて書いてみます。
めちゃくちゃ簡単に、ある日の時間vs風速の関係を分析してみることにしました。
ある意味、テーブルに相当するような機能を、ニューラルネットワークで組めるのか???
ということを実験してみるような感じです。
まずは前回作成したcsvファイルから、風速と時間部分だけ引っ張ってきます。
csvファイルには、ある一日分だけのデータが入っているものとします。
import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# deta making???
csv_input = pd.read_csv(filepath_or_buffer="data_out.csv", encoding="ms932", sep=",")
# インプットの項目数(行数 * カラム数)を返却します。
print(csv_input.size)
# 指定したカラムだけ抽出したDataFrameオブジェクトを返却します。
x = np.array(csv_input[["hour"]])
y = np.array(csv_input[["wind"]])
# 正規化
x_max = np.max(x,axis=0)
x_min = np.min(x,axis=0)
y_max = np.max(y,axis=0)
y_min = np.min(y,axis=0)
x = (x - np.min(x,axis=0))/(np.max(x,axis=0) - np.min(x,axis=0))
y = (y - np.min(y,axis=0))/(np.max(y,axis=0) - np.min(y,axis=0))
正規化したので、x、yともに[0,1]の間に数値が収まっています。
どんな具合か、ちょっとチェックしてみます。
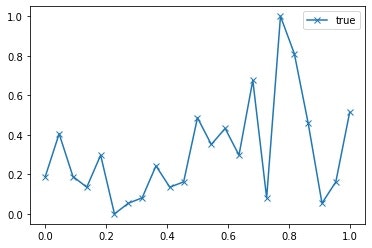
plt.plot(x,y,marker='x',label="true")
plt.legend()
プロットの点は、24つ、つまり、24時間分ということです。
各時間に1つの点だけがサンプルデータとして入力されています。
つまり、時系列の風速データということです。
こうやってみると、結構変動しているもんですね。
シンプルに考えると、これを24サンプルのテーブルと見なせば、横軸xの値から縦軸yを予測できます。
これをあえてニューラルネットワークのサンプルとして構築してみます。
色々と調べてみると、どうやらニューラルネットワーク・・・というか、ディープランニングはkerasというライブラリを使うとよいとのこと。
ただ、なんかインストールがトラぶってちょっとハマってしまったので、都合により、tensorflowに付属している
tensorflow.layers
というものを使ってみることにしました。
これなら、tensorflowさえ動けば、使えるようです。
今回構築したのは、シンプルな1層のニューラルネットワークです。
入力は1個、出力は1個、中間層のノード数は適当に。
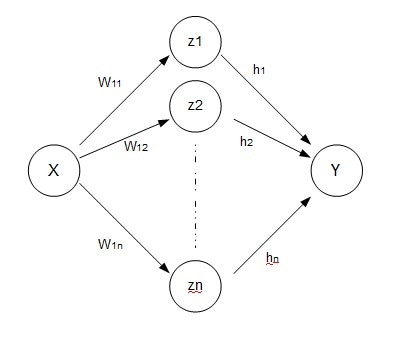
数式にすると、以下のようにyを推定します。
y = \sum_{k=1}^{N} \left( h_k \phi( z_k ) \right)\\
= \sum_{k=1}^{N} \left( h_k \phi( w_{1k}x + w_{2k}) \right)
ただし、Bias成分は図では省略していて、φは活性化関数です。
何でもよいんだろうけど、一旦シグモイド関数あたりを入れて考えてみます。
上記のニューラルネットワークのモデルは、tensorflow.layersでは以下のように構築できるようでした。
# make placeholder
x_ph = tf.placeholder(tf.float32, [None, 1])
y_ph = tf.placeholder(tf.float32, [None, 1])
# create newral parameter(depth=1,input:2 > output:1)
hidden1 = tf.layers.dense(x_ph, 24, activation=tf.nn.sigmoid)
newral_out = tf.layers.dense(hidden1, 1)
x_phが入力です。
newral_outが、x_phを元に計算したyの予測値ということになります。
ここでは使っていないy_phは、入力する正解値に使う予定です。
hidden1がzの層(中間層)です。
ノード数は24と適当に決めておきましたが、後からいくらでも変えられます。
たった2行でニューラルネットワークが組めるとは素晴らしいの一言ですね。
ここまで出来れば、後は最小化するパラメータを定義して、学習するループを組めばいけそうです。
以前使ったサンプルを再利用して、学習式???の部分は以下にしてみます。
# Minimize the mean squared errors.
loss = tf.reduce_mean(tf.square(newral_out - y_ph))
optimizer = tf.train.GradientDescentOptimizer(0.06)
train = optimizer.minimize(loss)
ループ部分は???
for k in range(10001):
if np.mod(k,1000) == 0:
# get Newral predict data
y_newral = sess.run( newral_out
,feed_dict = {
x_ph: x, # xに入力データを入れている
y_ph: y.reshape(len(y),1) # tに正解データを入れている
})
# errcheck??? ([newral predict] vs [true value])
err = y_newral - y
err = np.matmul(np.transpose(err),err)
# display err
print('[%d] err:%.5f' % (k,err))
# shuffle train_x and train_y
n = np.random.permutation(len(train_x))
train_x = train_x[n]
train_y = train_y[n].reshape([len(train_y), 1])
# execute train process
sess.run(train,feed_dict = {
x_ph: train_x, # x is input data
y_ph: train_y # y is true data
})
# check result infomation
y_newral = sess.run( newral_out
,feed_dict = {
x_ph: x, # xに入力データを入れている
y_ph: y.reshape(len(y),1) # tに正解データを入れている
})
# true info
plt.plot(x,y,marker='x',label="true")
# predict info
plt.plot(x,y_newral,marker='x',label="predict")
plt.legend()
おまけで、最終チェック用のプロットも入れてあります。
これで一通り揃いました。
動かしてみましょう。以下コンソール出力。
[0] err:12.74091
[1000] err:1.21210
[2000] err:1.21163
[3000] err:1.21162
[4000] err:1.21162
[5000] err:1.21161
[6000] err:1.21161
[7000] err:1.21161
[8000] err:1.21160
[9000] err:1.21160
[10000] err:1.21159
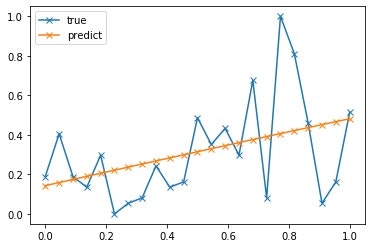
第一印象・・・マジか!!!!(がっかり)
ただの線形近似となっているようです。
動きを見てみると、errは徐々に減っていきながら収束しているので、学習自体は問題なさそうに見えます。
しかし、最終的に、err=1.2116ぐらいで収束しちゃっているみたいですね。
これだと、ニューラルネットワークを使う意味が全然無いです(笑)
zの出力をシグモイド関数にしたのがマズイのかと思い、ちょっと以下に設定を変えてみます。
hidden1 = tf.layers.dense(x_ph, 24, activation=tf.nn.relu)
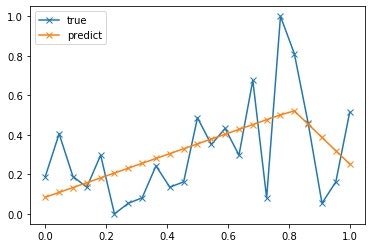
すると結果は?
[0] err:2.33927
[1000] err:1.18943
[2000] err:1.16664
[3000] err:1.13903
[4000] err:1.11184
[5000] err:1.09177
[6000] err:1.07951
[7000] err:1.06986
[8000] err:1.06280
[9000] err:1.05912
[10000] err:1.05760
うーむ、途中で折れてくれました(笑)
こんなものなのか???
これはこれでいいのかもしれませんが、最初の目的は ”テーブルの代わりの機能” だったので、ちょっと私がやりたいことと違っています。
tensorflow.layersのオプションなどを色々見てみましたが、ちょっといい方法が分からなかったので、ちょっと違うアプローチをしてみました。
いわゆるニューラルネットワークはどういう理論なのか???
これを調べる上で素晴らしいサイトがございました。
■ニューラルネットワークが任意の関数を表現できることの視覚的証明
https://nnadl-ja.github.io/nnadl_site_ja/chap4.html
Michael Nielsenさんの記事の翻訳だそうですが、本当に本質を突いた素晴らしい内容で、無料で見ていいのだろうか?というぐらいのものです。
詳しくは上記記事あたりを見るとよいのですが、ここでは重要な結論だけメモしておきます。
※任意の関数はステップ関数の和で表現できる
※中間層の2つのノードで、1つのステップ関数として機能できる
最初の、ステップ関数の和については、記事にはさらっとだけ書いてありました。
「ハーン・バナッハの定理」「リースの表現定理」という懐かしい名前が出てきてとても嬉しかったです(私は数学専攻でした)
これらの定理は、関数解析(関数の集合にtopologyを入れたときの理論)の中で出てきました。
ざっくり「ハーン・バナッハの定理」は拡張性、「リースの表現定理」は存在性を示していたと思います。
「リースの表現定理」が非常に美しい理論だったという印象だけがあります(笑)
ただ、個人的には、ステップ関数という時点で、ルベーグ積分の方のイメージが出てきて、いわゆるルベーグ積分可能な関数なら表現できるんだろうな~という拡大解釈をしてしまいました。
(ルベーグ積分は、収束するステップ関数が存在しているのが前提だったかな~)
ここまでは理論の世界ですが、重要なのは2個目。
中間層の2つのノードで1つのステップ関数として機能できる、という点でした。
つまり、パラメタを上手く決定すれば、ステップ関数の和としてニューラルネットワークを構築できるということ。
早速以下のようにパラメタを決定するファンクションを作ってみました。
def calc_b_w(s,sign):
N = 1000 # 仮置き
# s = -b/w
if sign > 0:
b = -N
else:
b = N
if s != 0:
w = -b/s
else:
w = 1
return b,w
def calc_w_h(x,y):
# xの昇順にソートされていて、x in [0,1]とする
K = len(x)
w_array = np.zeros([K*2,2])
h_array = np.zeros([K*2,1])
w_idx = 0
for k in range(K):
# x[k] , y[k]
if k > 0:
startX = x[k] + (x[k-1] - x[k])/2
else:
startX = 0
if k < K-1:
endX = x[k] + (x[k+1] - x[k])/2
else:
endX = 1
if k > 0:
b,w = calc_b_w(startX,1)
else:
b = 100
w = 1
# stepfunction 1stHalf
w_array[w_idx,0] = w
w_array[w_idx,1] = b
h_array[w_idx,0] = y[k]
w_idx += 1
# stepfunction 2ndHalf
b,w = calc_b_w(endX,1)
w_array[w_idx,0] = w
w_array[w_idx,1] = b
h_array[w_idx,0] = y[k]*-1
w_idx += 1
calc_b_wという関数では、ニューラルネットワークの入力層xから中間層zへの変換部分の係数を決定しています。
Nが大きくなるほど、ステップ関数に近づいていく、という仕様。
sが変化する点。(0<s<1)
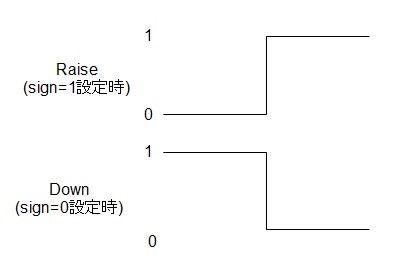
signは、+1か0が設定される仕様で、+1のときはRaise、0のときはDownとなります。
s=0.5のときの例を以下の絵に示します。
つまり、calc_b_wのアウトプットはあくまで大きさは+1のステップ関数の片側(増える側か減る側)となります。
これをRaiseのみですが2個組み合わせることによって、1つのステップ関数を構築します。
変化点をちょっとずらして、出力符号を逆転させたものを足すと、パルスっぽい波形ができます。
このままだと出力の大きさが1のままなので、適当に係数(hの部分)を掛けて完成です。
そして、calc_w_hに入力するx、yを元に、このパラメータを適当にふれるようにしました。
結果を確認してみます。
w_param,h_param = calc_w_h(x,y)
test_x = np.array(range(200))/200
test_y = np.zeros(len(test_x))
for k in range(len(test_x)):
test_y[k] = calc_New(test_x[k],h_param,w_param)
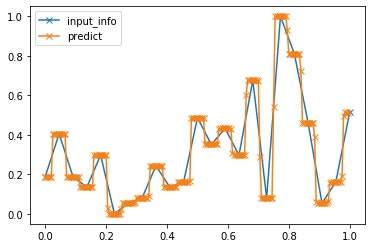
plt.plot(x,y,marker='x',label='input_info')
plt.plot(test_x,test_y,marker='x',label='predict')
plt.legend()
うまくステップ関数が構築できたようです。
なお、設定したパラメタ(w,h)を利用してニューラルネットワークの計算をする関数を以下のように定義しています。(超適当です、すみません)
def calc_New(x,h,w):
tmpx = np.array([x,1])
tmpx = tmpx.reshape(2,1)
longX = np.matmul(w,tmpx)
sigOUT = 1/(1+np.exp(-longX))
output = sigOUT * h
return np.sum( output )
以上で、完全一致に近いテーブルのようなニューラルネットワークが出来ました。
念のため上記を学習するプログラムとして動かしてみます。
さすがに大丈夫だと思いますが・・・
長々スミマセンが、一旦上記全部込みのソースを書いておきます。
import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
def calc_b_w(s,sign):
N = 1000 # 仮置き
# s = -b/w
if sign > 0:
b = -N
else:
b = N
if s != 0:
w = -b/s
else:
w = 1
return b,w
def calc_w_h(x,y):
# xの昇順にソートされていて、x in [0,1]とする
K = len(x)
w_array = np.zeros([K*2,2])
h_array = np.zeros([K*2,1])
w_idx = 0
for k in range(K):
# x[k] , y[k]
if k > 0:
startX = x[k] + (x[k-1] - x[k])/2
else:
startX = 0
if k < K-1:
endX = x[k] + (x[k+1] - x[k])/2
else:
endX = 1
if k > 0:
b,w = calc_b_w(startX,1)
else:
b = 100
w = 1
# stepfunction 1stHalf
w_array[w_idx,0] = w
w_array[w_idx,1] = b
h_array[w_idx,0] = y[k]
w_idx += 1
# stepfunction 2ndHalf
b,w = calc_b_w(endX,1)
w_array[w_idx,0] = w
w_array[w_idx,1] = b
h_array[w_idx,0] = y[k]*-1
w_idx += 1
return w_array,h_array
def calc_New(x,h,w):
tmpx = np.array([x,1])
tmpx = tmpx.reshape(2,1)
longX = np.matmul(w,tmpx)
sigOUT = 1/(1+np.exp(-longX))
output = sigOUT * h
return np.sum( output )
# deta making???
csv_input = pd.read_csv(filepath_or_buffer="data_out.csv", encoding="ms932", sep=",")
# インプットの項目数(行数 * カラム数)を返却します。
print(csv_input.size)
# 指定したカラムだけ抽出したDataFrameオブジェクトを返却します。
x = np.array(csv_input[["hour"]])
y = np.array(csv_input[["wind"]])
# num of records
N = len(x)
# 正規化
x_max = np.max(x,axis=0)
x_min = np.min(x,axis=0)
y_max = np.max(y,axis=0)
y_min = np.min(y,axis=0)
x = (x - np.min(x,axis=0))/(np.max(x,axis=0) - np.min(x,axis=0))
y = (y - np.min(y,axis=0))/(np.max(y,axis=0) - np.min(y,axis=0))
train_x = x
train_y = y
w_init,h_init = calc_w_h(x,y)
test_x = np.array(range(200))/200
test_y = np.zeros(len(test_x))
for k in range(len(test_x)):
#print('k=%d' % k)
test_y[k] = calc_New(test_x[k],h_init,w_init)
x_ph = tf.placeholder(tf.float32, [None, 2])
y_ph = tf.placeholder(tf.float32, [None, 1])
W = tf.Variable(w_init,dtype=tf.float32)
h = tf.Variable(h_init,dtype=tf.float32)
# Before starting, initialize the variables. We will 'run' this first.
init = tf.global_variables_initializer()
# Launch the graph.
sess = tf.Session()
sess.run(init)
longX = tf.transpose(tf.matmul(W,tf.transpose(x_ph)))
sigOUT = tf.math.sigmoid(longX)
output = tf.matmul(sigOUT,h)
loss = tf.reduce_mean(tf.square(output - y_ph))
optimizer = tf.train.GradientDescentOptimizer(0.05)
train = optimizer.minimize(loss)
plt.plot(x,y,marker='x',label="true")
for k in range(201):
if np.mod(k,10) == 0:
#if 1:
# get Newral predict data
tmpX = np.hstack([x,np.ones(N).reshape([N,1])])
err = sess.run( loss
,feed_dict = {
x_ph: tmpX, # xに入力データを入れている
y_ph: y.reshape(len(y),1) # tに正解データを入れている
})
print('[%d] err:%.5f' % (k,err))
if np.mod(k,100) == 0 and k > 0:
tmpX = np.hstack([x,np.ones(N).reshape([N,1])])
newral_y = sess.run(output,feed_dict = {
x_ph: tmpX, # x is input data
y_ph: train_y # y is true data
})
plt.plot(x,newral_y,marker='x',label="k=%d" % k)
# shuffle train_x and train_y
n = np.random.permutation(len(train_x))
train_x = train_x[n]
train_y = train_y[n].reshape([len(train_y), 1])
tmpX = np.hstack([train_x,np.ones(N).reshape([N,1])])
# execute train process
sess.run(train,feed_dict = {
x_ph: tmpX, # x is input data
y_ph: train_y # y is true data
})
plt.legend()
結果は???
[0] err:0.00287
[10] err:0.00172
[20] err:0.00134
[30] err:0.00111
[40] err:0.00094
[50] err:0.00081
[60] err:0.00070
[70] err:0.00061
[80] err:0.00054
[90] err:0.00048
[100] err:0.00043
[110] err:0.00038
[120] err:0.00034
[130] err:0.00031
[140] err:0.00028
[150] err:0.00025
[160] err:0.00023
[170] err:0.00021
[180] err:0.00019
[190] err:0.00018
[200] err:0.00016
ほぼほぼゼロに収束してくれました!素晴らしい。
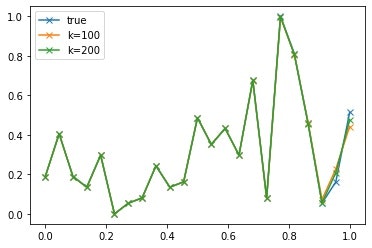
グラフも以下のような感じで、目視ではほぼ一致です。
(なんか最後の点の初期値がバグってますね・・・)
これで無事テーブル機能を実装できました。
通常の機械学習では有り得ないようなアプローチでしたが、初期値さえ上手く設定できれば、これぐらいのことは全然問題なく出来るんですね。
ただ、恐らくこれは、一般的には過学習と呼ばれる現象になっていると思われます。
あくまで練習用ということで、ご覧頂けたらと思います。
次もこのテーマの続きをもうちょっとだけ書いてみる予定です。