今回の目標
誤差逆伝播法を実装します。
この記事は、こちらの文献を参考にさせていただきました。
まずは勾配降下法。
ここから本編
誤差逆伝播法のまとめ
勉強不足だったので備忘録も兼ねて書いておきます。
下付き文字ですが、「pre」が前の層、「next」が次の層、「now」もしくは何も書いていなければ現在着目している層、「last」が最終層(出力層)を指します。下付き文字がコンマで区切られて二つある場合、二つ目はその層の何番目のノードのものであるかを指します。
また、「old」が更新前のパラメータ、「new」が更新後のパラメータです。
一般的に他の文献では層の数が上付き文字であらわされることが多いですが、累乗と区別がつかずわかりにくいのでここでは用いません。
勾配降下法
誤差を$\mathbf E$、重みを$\mathbf w$、学習率を$\eta$とすると、勾配降下法は
$$
\mathbf w_{new} = \mathbf w_{old} - \eta \frac{\partial \mathbf E}{\partial \mathbf w_{old}}
$$
と表せられます。$\mathbf w_{old}$はわかっていますので、$\mathbf w_{new}$を求めるうえで未知数となるのは右辺第二項の分数部分です。
ここで、連鎖律を用いることで、
$$
\frac{\partial \mathbf E}{\partial \mathbf w_{old}} = \frac{\partial \mathbf E}{\partial \mathbf x}\frac{\partial \mathbf x}{\partial \mathbf w_{old}}
$$
と式変形できます。ここで$\mathbf x$は、ノードでの線形変換後の値です。なぜそんな値を選んだのかというと、おそらく後の計算がうまくいくからだと思います。
そして、繰り返しになりますが$\mathbf x$は前の層の出力にそのノードの重みをかけたものですので、層の出力を$\mathbf a$とおくと
$$
\frac{\partial \mathbf x_{now}}{\partial \mathbf w_{old}} = \mathbf a_{pre}
$$
となります。$\mathbf a_{pre}$を$\mathbf w_{old}$で線形変換したものが$\mathbf x_{now}$ですから、上の式になるのは当然ですね。このあたり、どれがどの値なのか混乱したので気を付けてください。
これを連鎖律の式の右辺第二項に代入すると
$$
\frac{\partial \mathbf E}{\partial \mathbf w_{old}} = \frac{\partial \mathbf E}{\partial \mathbf x_{now}}\mathbf a_{pre}
$$
と変形できます。式を簡単にするために、
$$
\mathbf \delta = \frac{\partial \mathbf E}{\partial \mathbf x_{now}}
$$
と置きます。すると連鎖律の式は以下のように、簡単に表記できます。
$$
\frac{\partial \mathbf E}{\partial \mathbf w_{old}} = \mathbf \delta \mathbf a_{pre}
$$
これで、未知数は$\mathbf \delta$のみとなりました。
デルタを求める
ここで、$\mathbf \delta$は最終層とそれ以外の層で求め方が変わります。
最終層
まず最終層での求め方を見ていきます。
$$
\mathbf \delta_{last} = \frac{\partial \mathbf E}{\partial \mathbf x_{last}}
$$
上に書いたのは$\mathbf \delta$の定義です。連鎖律から、
$$
\mathbf \delta_{last} = \frac{\partial \mathbf E}{\partial \mathbf a_{last}}\frac{\partial \mathbf a_{last}}{\partial \mathbf x_{last}}
$$
がいえます。ここで$\mathbf a$は、ここでは最終層の出力です。ここで、右辺一つ目の分数を見てますと、
$$
\frac{\partial \mathbf E}{\partial \mathbf a_{last}} = \frac{\partial E(\mathbf a_{last})}{\partial \mathbf a_{last}} = E'(\mathbf a_{last})
$$
となります。ここで、$E()$は誤差関数です。平均二乗誤差とか、平均絶対誤差とかその辺です。誤差関数の引数は最終層の出力ですから、上式が成り立つのは当然です。
たとえば平均二乗誤差なら、正解を$\mathbf t$、データ数を$N$とおくと
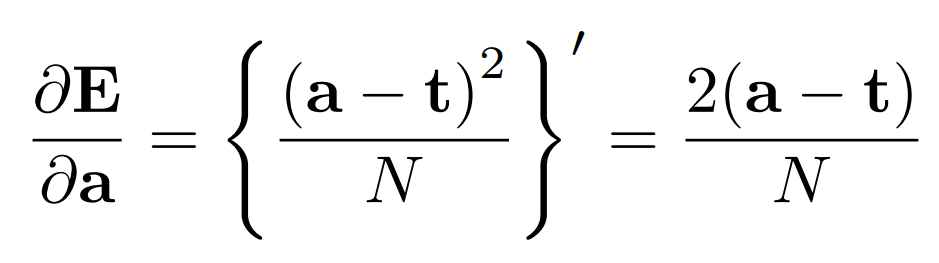
のようになります(なぜか$\LaTeX$のコンパイルが通らなかったので画像を貼りました)。
次に、右辺二つ目の分数を変形します。出力層の活性化関数を$f()$とおくと、
$$
\frac{\partial \mathbf a_{last}}{\partial \mathbf x_{last}} = \frac{\partial f(\mathbf x_{last})}{\partial \mathbf x_{last}} = f'(\mathbf x_{last})
$$
となります。この層の出力$\mathbf a_{last}$は、この層の線形変換後の値$\mathbf x_{last}$を活性化関数に投げたものですので、上の式が成り立ちます。繰り返しになりますが、$\mathbf x_{last}$は各ノードでの線形変換後、活性化関数にかける前の行列です。活性化関数はReLuとかsigmoidとかです。例えばReLuなら、
$$
\frac{\partial \mathbf a}{\partial \mathbf x} = ReLu'(\mathbf x)
$$
とでも書くのでしょうか。
入力が0未満の時、
$$
\frac{\partial \mathbf a}{\partial \mathbf x} = 0
$$
入力が0以上の時、
$$
\frac{\partial \mathbf a}{\partial \mathbf x} = 1
$$
のようになります。
式をまとめると、
$$
\mathbf \delta_{last} = E'(\mathbf a_{last})f'(\mathbf x_{last})
$$
となります。全て既知関数ですので、これで$\mathbf \delta_{last}$を求められます。$\mathbf \delta_{last}$を求められるということは、$\frac{\partial \mathbf E}{\partial \mathbf w_{old}}$が求められるということであり、$\frac{\partial \mathbf E}{\partial \mathbf w_{old}}$が求められるということは、冒頭で示した勾配降下法の式の中から未知数がなくなるということです。これで、最終層の重みが更新できることになります。
また、上式を見ればわかる通り、勾配降下法をプログラムで実現するなら誤差関数の微分関数と活性化関数の微分関数がそれぞれ必要になるということになります。さらに、各ノードの線形変換後の値や出力も保持する必要があります。
また、回帰であれば出力層はこの式一つだけですが、分類の場合はノードごとにこれがあることになります。$\mathbf a_{last}$は一つの層に一つしかないですが、$\mathbf x_{last}$はノードの数だけあります。
最終層以外
次に、最終層以外の$\mathbf \delta$について見ていきます。
$$
\mathbf \delta = \frac{\partial \mathbf E}{\partial \mathbf x_{now}}
$$
上に書いたのは$\mathbf \delta$の定義です。
次の層のノード数を$m$とし、連鎖律を用いると、
$$
\mathbf \delta = \frac{\partial \mathbf E}{\partial \mathbf x_{now}} = \sum\limits_{n=1}^m\frac{\partial \mathbf E}{\partial \mathbf x_{next, n}}\frac{\partial \mathbf x_{next, n}}{\partial \mathbf a_{now}}\frac{\partial \mathbf a_{now}}{\partial \mathbf x_{now}}
$$
がいえます。ここで、$\mathbf a$及び$\mathbf x$は今までどおり、層の出力及びノード内での線形変換後の値です。
次の層のノードの値を合計する理由を説明します。現在全結合層を考えているため、このノードの重みは、巡り巡って次の層のすべてのノードに影響を与えるからです。では、なぜ足し算なのでしょうか。これには数学的な理由が絡んでいます。それを説明するために、まず以下の式を見てください。
$$
\frac{\partial \mathbf E}{\partial \mathbf x_{now}} = \frac{\partial \mathbf E}{\partial \mathbf x_{next}}\frac{\partial \mathbf x_{next}}{\partial \mathbf x_{now}}
$$
これは、先ほど$\mathbf \delta$を変形した式と違い、連鎖律を一回だけ使ったようなものだと納得してください。ただし、厳密にいえば正しい式ではありません。なぜなら$\mathbf x_{next}$はノードごとに異なる値を持つため、ここでの$\mathbf E$は多変数関数となるからです。よって合成関数の微分が必要となり、シグマ記号が必要になるというわけです。
話を戻します。先ほど示した式、
$$
\mathbf \delta = \frac{\partial \mathbf E}{\partial \mathbf x_{now}} = \sum\limits_{n=1}^m\frac{\partial \mathbf E}{\partial \mathbf x_{next, n}}\frac{\partial \mathbf x_{next, n}}{\partial \mathbf a_{now}}\frac{\partial \mathbf a_{now}}{\partial \mathbf x_{now}}
$$
はなんだか長いし複雑ですので、最終層の時と同様に簡単な値にまとめていきます。
ここで右辺一つ目の分数は、定義より、
$$
\frac{\partial \mathbf E}{\partial \mathbf x_{next, n}} = \mathbf \delta_{next, n}
$$
が言えます。最終層の一つ手前の層なら最終層の値が入ります。最終層での$\mathbf \delta$の求め方はすでに導出していますので、連鎖的にすべての層の$\frac{\partial \mathbf E}{\partial \mathbf x_{next, n}}$がこれで求められます。
次に二つ目の分数を見ます。次の層の重みを$\mathbf w_{next, n}$とおくと、
$$
\frac{\partial \mathbf x_{next, n}}{\partial \mathbf a_{now}} = \mathbf w_{next, n}
$$
がいえます。$\mathbf x_{next, n}$は$\mathbf a_{now}$を$\mathbf w_{next, n}$で線形変換した値ですので、上式が成り立ちます。当然$\mathbf w_{next, n}$は既知ですから、$\frac{\partial \mathbf x_{next, n}}{\partial \mathbf a_{now}}$もこれで求められます。
最後に三つ目の分数を見ます。
$$
\frac{\partial \mathbf a_{now}}{\partial \mathbf x_{now}} = f'(\mathbf x)
$$
最終層でもこの変形は登場しました。$\mathbf a_{now}$は$\mathbf x_{now}$を活性化関数に入れたものですので、当然上式は成り立ちます。そして活性化関数は当然既知ですから(自分で設定しますからね)、$\mathbf \delta$を求めるうえですべての未知数が消えたことになります。つまり、最終層以外では、
$$
\mathbf \delta = \sum\limits_{n=1}^{m}\mathbf \delta_{next, n} \mathbf w_{next, n}f'(\mathbf x)
$$
となります。これをプログラムで実現するなら、各ノードは自分の$\mathbf \delta$を保持せねばならないと分かります。
まとめ
これで最終層、そして最終層以外の$\mathbf \delta$が求められるようになりましたから、
$$
\frac{\partial \mathbf E}{\partial \mathbf w_{old}} = \mathbf \delta \mathbf a_{pre}
$$
が求められるようになり、これを勾配降下法の式
$$
\mathbf w_{new} = \mathbf w_{old} - \eta \frac{\partial \mathbf E}{\partial \mathbf w_{old}}
$$
に代入することで重みの更新ができるようになります。
実際に代入すると、最終層では
$$
\mathbf w_{new} = \mathbf w_{old} - \eta E'(\mathbf a_{last})f'(\mathbf x_{last})\mathbf a_{pre}
$$
最終層以外では
$$
\mathbf w_{new} = \mathbf w_{old} - \eta \sum\limits_{n=1}^{m}\mathbf \delta_{next, n} \mathbf w_{next, n}f'(\mathbf x_{now})\mathbf a_{pre}
$$
となります。
現在のディレクトリ構成
「optimizer」を、今までずっと「optimzer」と間違えて書いていたので修正しました。
MyNet
├── costFunction // 損失関数
├── layer // 層
├── matrix // 行列
├── network // ネットワーク
├── nodes // ノード
│ └── activationFunction // 活性化関数
└── optimizer // 最適化(今回作成)
修正点
Networkクラスをいじりました。
まず、以下のフィールドを追加。
/** Number of input variables for this network. */
int input_num;
それに伴い、コンストラクタも若干変更。「this.input_num = ~」の行を追加しました。
また、ノードのインスタンス化時に乱数のseed値をノードごとに変更するためコンストラクタにnumを追加しました。ノードのコンストラクタについては後述。
/**
* Constructor for this class.
* @param input_num number of input.
* @param layers Each layers.
*/
public Network(int input_num, Layer ... layers){
for (int i = 0; i < layers.length; i++){
if (layers[i].nodes[0] != null){
System.out.println("Wrong constractor.");
System.exit(-1);
}
}
this.input_num = input_num;
this.layers = new Layer[layers.length];
for (int i = 0; i < this.layers.length; i++){
this.layers[i] = layers[i].clone();
}
int num = 0;
for (int i = 0; i < this.layers.length; i++){
AF type = this.layers[i].AF;
for (int j = 0; j < this.layers[i].nodes.length; j++){
this.layers[i].nodes[j] = new Node(input_num, type, num);
num++;
}
input_num = this.layers[i].nodes_num;
}
this.layers_num = this.layers.length;
}
後で使うため、空のコンストラクタを追加しました。事故を防ぐためprivateです。
/**
* Constructor for this class.
*/
private Network(){
;
}
cloneメソッドを追加。
層の中のノードも含め、全てのフィールドをインスタンス化せずに空のネットワークを作成し、その後に層、ノードの順にインスタンス化しています。
理由は、入力層以外の各層の入力数が前の層のノード数に依存するために、一度にすべてインスタンス化できないからです。正規のコンストラクタでは各層の入力数を指定せずに済むようにしています。詳しくは42 ~ネットワーク~を参照。
@Override
public Network clone(){
Network rtn = new Network();
rtn.input_num = this.input_num;
rtn.layers = new Layer[this.layers.length];
for (int i = 0; i < this.layers.length; i++){
rtn.layers[i] = this.layers[i].clone();
}
int num = 0;
for (int i = 0; i < this.layers.length; i++){
AF type = this.layers[i].AF;
for (int j = 0; j < this.layers[i].nodes.length; j++){
this.layers[i].nodes[j] = new Node(this.input_num, type, num);
num++;
}
this.input_num = this.layers[i].nodes_num;
}
rtn.layers_num = this.layers_num;
return rtn;
}
ただ、作ったはいいんですがネットワーククラスのこれらの変更は結局使いませんでした。
今更ですが、活性化関数としてLinerを追加しました。
package nodes.activationFunction;
/**
* Liner function.
*/
public class Liner extends ActivationFunction {
/**
* Constructor for this class.
* Nothing to do.
*/
public Liner(){
;
}
@Override
public String toString(){
return "Liner";
}
}
MatrixクラスのfillメソッドをfillNumに改名しました。
また、fillRandomメソッド、fillNextRnadomメソッドを新規で作成しました。
/**
* Fill this matrix with a number.
* @param num Number to fill.
*/
public void fillNum(double num){
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = num;
}
}
}
/**
* Fill this matrix with random numbers has range 0~1.
*/
public void fillNextRandom(){
Random rand = new Random(0);
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = rand.nextDouble();
}
}
}
/**
* Fill this matrix with random number has range min~max.
* @param min Number of min for range.
* @param max Number of max for range.
*/
public void fillRandom(double min, double max){
Random rand = new Random(0);
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = rand.nextDouble()*(max-min) + min;
}
}
}
/**
* Fill this matrix with random numbers has range 0~1.
* @param num Number of seed.
*/
public void fillNextRandom(int num){
Random rand = new Random(num);
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = rand.nextDouble();
}
}
}
/**
* Fill this matrix with random number has range min~max.
* @param min Number of min for range.
* @param max Number of max for range.
* @param num Number of seed.
*/
public void fillRandom(double min, double max, int num){
Random rand = new Random(num);
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = rand.nextDouble()*(max-min) + min;
}
}
}
さらに、Matrixクラスに以下のメソッドを追加しました。
/**
* Power of a matrix element.
* @param matrix A Matrix instance.
* @return Multiplying a matrix by itself.
*/
public static Matrix pow(Matrix matrix){
Matrix rtn = matrix.clone();
for (int i = 0; i < rtn.row; i++){
for (int j = 0; j < rtn.col; j++){
rtn.matrix[i][j] = Math.pow(rtn.matrix[i][j], 2);
}
}
return rtn;
}
/**
* Power of this matrix element.
*/
public void pow(){
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = Math.pow(this.matrix[i][j], 2);
}
}
}
/**
* Power of a matrix element.
* @param matrix A Matrix instance.
* @param num Number to a power.
* @return Powered a matrix by itself.
*/
public static Matrix pow(Matrix matrix, int num){
Matrix rtn = matrix.clone();
for (int i = 0; i < rtn.row; i++){
for (int j = 0; j < rtn.col; j++){
rtn.matrix[i][j] = Math.pow(rtn.matrix[i][j], num);
}
}
return rtn;
}
/**
* Power of this matrix element.
* @param num Number to a power.
*/
public void pow(int num){
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = Math.pow(this.matrix[i][j], num);
}
}
}
/**
* Get a single column matrix from a matrix.
* @param in Matrix instance.
* @param num Number of column that extract.
* @return Extracted matrix.
*/
public static Matrix getCol(Matrix in, int num){
Matrix rtn = new Matrix(new double[in.row][1]);
for (int i = 0; i < in.row; i++){
rtn.matrix[i][0] = in.matrix[i][num];
}
return rtn;
}
/**
* Get a single column matrix from this matrix.
* @param num Number of column that extract.
* @return Extracted matrix.
*/
public Matrix getCol(int num){
Matrix rtn = new Matrix(new double[this.row][1]);
for (int i = 0; i < this.row; i++){
rtn.matrix[i][0] = this.matrix[i][num];
}
return rtn;
}
/**
* Get a single row matrix from a matrix.
* @param in Matrix instance.
* @param num Number of row that extract.
* @return Extracted matrix.
*/
public static Matrix getRow(Matrix in, int num){
Matrix rtn = new Matrix(new double[1][in.col]);
for (int i = 0; i < in.col; i++){
rtn.matrix[0][i] = in.matrix[num][i];
}
return rtn;
}
/**
* Get a single row matrix from this matrix.
* @param num Number of row that extract.
* @return Extracted matrix.
*/
public Matrix getRow(int num){
Matrix rtn = new Matrix(new double[1][this.col]);
for (int i = 0; i < this.col; i++){
rtn.matrix[0][i] = this.matrix[num][i];
}
return rtn;
}
multメソッドにミスがあったので修正しました。
/**
* Multiply this matrix by a number.
* @param num Number.
*/
public void mult(double num){
for (int i = 0; i < this.row; i++){
for (int j = 0; j < this.col; j++){
this.matrix[i][j] = this.matrix[i][j] * num;
}
}
}
Nodeクラスのコンストラクタで、重みの初期値を乱数にできるようにしました。
また、デルタなどを追加しました。
また、損失関数と区別するため、ノードクラス内の活性化関数の名前を「function」から「aFunc」に変更しました。
/** Valiable for back propagation. */
public Matrix delta;
/** Matrix linear transformed. */
public Matrix x;
/** Matrix of output from this node. */
public Matrix a;
/**
* Constructor for this class.
* Number of inputs includes bias.
* @param input_num Number of inputs.
* @param type Type of activation function.
* @exception System.exit The specified activation function
* does not exist or misspecified.
*/
public Node(int input_num, AF type){
in += input_num;
w = new Matrix(new double[in][1]);
w.fillNum(0.5);
// w.fillRandom(-1., 1.);
switch (type) {
case RELU:
aFunc = new ReLu();
break;
case SIGMOID:
aFunc = new Sigmoid();
break;
case TANH:
aFunc = new Tanh();
break;
case LINER:
aFunc = new Liner();
break;
default:
System.out.println("ERROR: The specified activation function is wrong");
System.exit(-1);
}
}
/**
* Constructor for this class.
* Number of inputs includes bias.
* @param input_num Number of inputs.
* @param type Type of activation function.
* @param num Number of seed.
* @exception System.exit The specified activation function
* does not exist or misspecified.
*/
public Node(int input_num, AF type, int num){
in += input_num;
w = new Matrix(new double[in][1]);
// w.fillNum(0.5);
w.fillRandom(-1., 1., num);
switch (type) {
case RELU:
aFunc = new ReLu();
break;
case SIGMOID:
aFunc = new Sigmoid();
break;
case TANH:
aFunc = new Tanh();
break;
case LINER:
aFunc = new Liner();
break;
default:
System.out.println("ERROR: The specified activation function is wrong");
System.exit(-1);
}
}
活性化関数に微分を追加しました。線形変換後の値で微分しますので、$x$で微分します。
まず親クラスですが、親クラスのメソッドはLinerクラスでそのまま使おうと思うのでLinearの微分です。
$$
f(x) = x
$$$$
f'(x) = 1
$$
/**
* Calcurate this activation function's differential.
* @param matrix Matrix of input.
* @return The result of differentiating this activation function.
*/
public Matrix differential(Matrix matrix){
Matrix rtn = matrix.clone();
rtn.fillNum(1.0);
return rtn;
}
ReLu関数。こちらも、Qiitaの$\LaTeX$がなぜかコンパイル通らなかったので写真です。
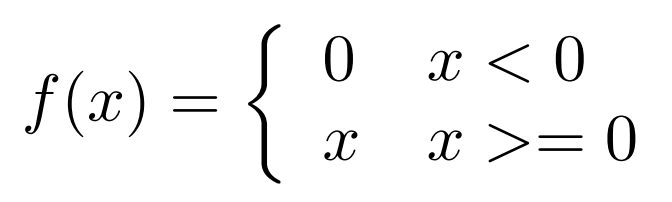
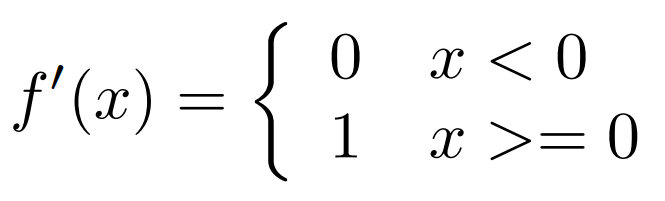
/**
* Calcurate this activation function's differential.
* @param matrix Matrix of input.
* @return The result of differentiating this activation function.
*/
public Matrix differential(Matrix matrix){
Matrix rtn = matrix.clone();
for (int i = 0; i < rtn.row; i++){
for (int j = 0; j < rtn.col; j++){
if (rtn.matrix[i][j] < 0){
rtn.matrix[i][j] = 0;
}else{
rtn.matrix[i][j] = 1.0;
}
}
}
return rtn;
}
シグモイド関数。
$$
f(x) = \frac{1}{1+e^{-x}}
$$$$
f'(x) = \left(1-\frac{1}{1+e^{-x}}\right)\frac{1}{1+e^{-x}}
$$
/**
* Calcurate this activation function's differential.
* @param matrix Matrix of input.
* @return The result of differentiating this activation function.
*/
public Matrix differential(Matrix matrix){
Matrix rtn = matrix.clone();
for (int i = 0; i < rtn.row; i++){
for (int j = 0; j < rtn.col; j++){
rtn.matrix[i][j] = (1 - 1/(1+Math.exp(-matrix.matrix[i][j])))
/ (1 + Math.exp(-matrix.matrix[i][j]));
}
}
return rtn;
}
ハイパボリックタンジェント。
$$
f(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
$$$$
f'(x) = 1-\tanh ^2(x)
$$
/**
* Calcurate this activation function's differential.
* @param matrix Matrix of input.
* @return The result of differentiating this activation function.
*/
public Matrix differential(Matrix matrix){
Matrix rtn = this.calcurate(matrix);
rtn.pow();
rtn.mult(-1);
return Matrix.add(rtn, 1.0);
}
損失関数にも微分を追加します。そのノードの出力で微分しますので、説明で使用した記号で言うと$a$で微分します。プログラム内だと$y$と記述しています。
親クラスは適当。どうせ使わないので。
/**
* Calcurate this cost function's differential.
* @param y Matrix of network's output.
* @param t Matrix of actual data.
* @return The result of differentiating the difference between y and t.
*/
public Matrix differential(Matrix y, Matrix t){
return Matrix.sub(y, t);
}
平均絶対誤差。
$$
E(y) = \frac{1}{N}\sum\limits_{n=1}^{N}|y_t-t_n|
$$
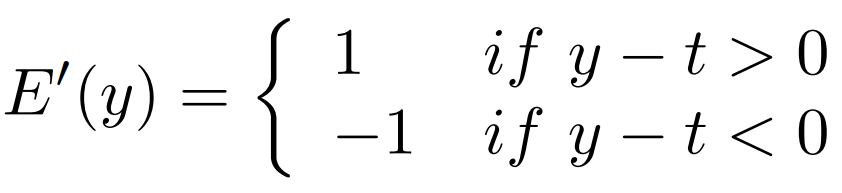
画像の式は、厳密には正しくないですが分かりやすさ重視ということで・・・。
/**
* Calcurate this cost function's differential.
* @param y Matrix of network's output.
* @param t Matrix of actual data.
* @return The result of differentiating the MAE between y and t.
*/
public Matrix differential(Matrix y, Matrix t){
Matrix rtn = new Matrix(t);
for (int i = 0; i < t.row; i++){
for (int j = 0; j < t.col; j++){
if (y.matrix[i][j] - t.matrix[i][j] > 0){
t.matrix[i][j] = 1.0;
}else{
t.matrix[i][j] = -1.0;
}
}
}
return rtn;
}
平均二乗誤差。
$$
E(y) = \frac{1}{N}\sum\limits_{n=1}^{N}(y_n-t_n)^2
$$$$
E'(y) = \frac{2}{N}\sum\limits_{n=1}^{N}(y_n-t_n)
$$
/**
* Calcurate this cost function's differential.
* @param y Matrix of network's output.
* @param t Matrix of actual data.
* @return The result of differentiating the MSE between y and t.
*/
public Matrix differential(Matrix y, Matrix t){
Matrix rtn = Matrix.sub(y, t);
rtn.meanCol();
rtn.mult(2);
return rtn;
}
平均平方二乗誤差。
$$
E(y) = \frac{1}{N}\sqrt{\sum\limits_{n=1}^{N}(y_n-t_n)^2}
$$
微分方法が分かりませんので、解決次第追記します。
実装方針
誤差逆伝播法をどう実装するか悩みましたが、新しくそれ用のクラスを作成し、その中にネットワーククラスや損失関数クラスをまとめパラメータ更新をすることにしました。
たぶんですが、chainerもそんな感じなんじゃないでしょうか。
Optimizer.java
まず最適化の親クラス。正直、あまり必要ない気はしますが・・・。
package optimizer;
import network.*;
import costFunction.*;
/**
* Parent class of optimizer.
*/
public class Optimizer {
/** Network to which optimization is applied. */
Network net;
/** Learning rate. */
double eta = 0.01;
/** Cost function of this network. */
CostFunction cFunction;
/**
* Constructor for this class.
*/
protected Optimizer(){
;
}
}
GradientDescent.java
勾配降下法。いわゆるSGD、確率的勾配降下法の原型です。
ここで、GradientDescentクラスはネットワークをフィールドとして所持しています。当然ネットワークの中には層があり、層の中にはノードがあり、層の中には重み行列が存在します。つまりこのクラスからネットワーク全体を俯瞰することができます。
なので、ここからすべてのパラメータを調整することにします。
また、誤差逆伝播法に直接かかわる修正点について以下に記載します。
コンストラクタなどについて、以下に載せておきます。
もともとネットワーククラスをcloneする予定でしたが、よく考えたらそんなことする必要ないので参照代入してます。
package optimizer;
import network.*;
import costFunction.*;
import matrix.*;
import layer.*;
import nodes.*;
/**
* Class for GD.
*/
public class GradientDescent extends Optimizer{
/**
* Constructor for this class.
*/
public GradientDescent(){
;
}
/**
* Constructor for this class.
* @param net Network to which optimization is applied.
*/
public GradientDescent(Network net, CostFunction f){
this.net = net;
this.cFunc = f;
}
/**
* Constructor for this class.
* @param net Network to which optimization is applied.
* @param eta Learning rate.
*/
public GradientDescent(Network net, CostFunction f, double eta){
this.net = net;
this.cFunc = f;
this.eta = eta;
}
/**
* Doing forward propagation.
* @param in input matrix.
* @return Matrix instance of output.
*/
public Matrix forward(Matrix in){
return this.net.forward(in);
}
また、各ノードはそれぞれ自分に関する情報しか保持していないので、上の説明で用いた$\mathbf a$、つまり 層の出力 は誰も持っていません。自分の出力なら保持しています。
なのでそれを作成するメソッドを準備しました。
/**
* Calcurate output of a layer.
* @param nodes Nodes in the layer.
* @return Output of the layer.
*/
public Matrix calA(Node[] nodes){
Matrix rtn = new Matrix(new double[nodes[0].a.row][nodes.length]);
for (int i = 0; i < rtn.row; i++){
for (int j = 0; j < rtn.col; j++){
rtn.matrix[i][j] = nodes[j].a.matrix[i][0];
}
}
return Matrix.appendCol(rtn, 1.0);
}
また、詳しくは後述しますがこちらのメソッドを作成しました。
/**
* Get a matrix of weights related to the output of a node.
* @param nodes Nodes of next layer.
* @param num Number of the node.
* @return Matrix instance.
*/
public Matrix calW(Node[] nodes, int num){
Matrix rtn = new Matrix(new double[nodes.length][1]);
for (int i = 0; i < nodes.length; i++){
rtn.matrix[i][0] = nodes[i].w.matrix[num][0];
}
return rtn;
}
修正点
Nodeクラス。
順方向計算メソッド内で、線形変換後と出力値をそれぞれ保持してもらいます。
また、警告文を削除しました。どうせ内積計算でチェックするので冗長設計でした。
/**
* Doing forward propagation.
* @param input Array of inputs.
* @return output array's element.
*/
public Matrix forward(Matrix input){
// 削除部分
// if (input.col != w.row){
// System.out.println("node forward error");
// System.exit(-1);
// }
this.x = Matrix.dot(input, w);
this.a = aFunc.calcurate(x);
return a.clone();
}
最終層
最終層での重み更新の式をもう一度貼ります。
$$
\mathbf w_{new} = \mathbf w_{old} - \eta E'(\mathbf a_{last})f'(\mathbf x_{last})\mathbf a_{pre}
$$
ここで$\eta$は学習率で、これは最適化クラスがdoubleで保持しています。
$E'$は損失関数の微分で、損失関数クラスがメソッドとして保持しています。
$\mathbf a_{last}$は出力層からの出力で、ノードクラスがMatrixインスタンスとして保持しています。
$f'$は活性化関数の微分で、活性化関数クラスがメソッドとして保持しています。
$\mathbf x_{last}$は出力層での線形変換後の値(活性化関数に入れる前の値)です。これは出力と同様ノードクラスがMatrixインスタンスとして保持しています。
$\mathbf a_{pre}$は前の層の出力で、こちらもノードクラスがMatrixインスタンスとして保持しています。
この式を、最終層で、ノードの数だけ繰り返す必要があります。
また、最終層でのデルタは
$$
\mathbf \delta_{last} = E'(\mathbf a_{last})f'(\mathbf x_{last})
$$
です。
上式をプログラムで再現します。
なお、当然ですがすでに最低一回は順方向計算を行っている前提で誤差逆伝播メソッドを作成します。
誤差逆伝播法はbackという名前のメソッドで実装しました。
まず、その最終層部分を記載します。
/**
* Doing back propagation.
* @param x Input layer.
* @param y Result of forward propagation.
* @param t Answer.
*/
public void back(Matrix x, Matrix y, Matrix t){
// last layer
// 今着目している層(ここでは最終層)
Layer nowLayer = this.net.layers[this.net.layers_num-1];
// 今着目している層の前の層
Layer preLayer = this.net.layers[this.net.layers_num-2];
// 最終層のノードの数だけ繰り返す
for (int i = 0; i < nowLayer.nodes.length; i++){
// 現在着目しているノード
Node nowNode = nowLayer.nodes[i];
// 計算用
Matrix cal;
// E'(a)
cal = this.cFunc.differential(nowNode.a, t.getCol(i));
// E'(a)f'(x) ※これが最終層のデルタ
cal = Matrix.dot(cal.T(), nowNode.aFunc.differential(nowNode.x));
nowNode.delta = cal.matrix[0][0];
// E'(a)f'(x)a
cal = Matrix.mult(this.calA(preLayer.nodes), nowNode.delta);
// -ηE'(a)f'(x)a
cal.mult(-this.eta);
// w-ηE'(a)f'(x)a
nowNode.w.add(cal.meanCol().T());
}
コメントの量が多くて申し訳ありませんが、コメントなしの方が分かりにくそうだったので追加しました。
データ数をNとおきますと、
$$
E'(a_{last})
$$
の結果はN行1列になります。ここで、aは層の出力ですが、ノードごとにデルタの計算をするためプログラム内ではそのノードの出力を使っています。また、プログラム内でtも入力しているのは、微分の関係上必要になるからです。
次に、
$$
E'(a_{last})f'(x_{last})
$$
を計算します。$f'(x_{last})$もN行1列になる(xは各ノード・各データにつき、一つしかありません)ので、普通に内積して結果はスカラとなります。
aは前の層の出力です。前の層のノード数が例えば4だった場合、N行5列となります(バイアスも含むため)。これをデータごとに平均します。なぜ平均するかについて説明します。
実はこの平均については、「おそらくこうだろう」という予想の元行っています。というのも、参考にさせていただいた文献ではデータ1セットごとに誤差逆伝播法を使っているものしかなく、GDのように複数のデータから勾配を更新する具体的な方法は分かりませんでした。
しかし、重みを更新するためには計算式の右辺第二項部分が二次元行列ではつじつまが合いませんので、おそらく平均だろう、と考えています。もし間違えがあれば教えてください。
本題に戻りまして、データごとに平均したことでaは1行5列となりました。この層の重みは5行1列ですので、学習率かけて転置させて引けば重みが更新されます。
中間・入力層
中間層及び入力層での重み更新式とデルタ計算式は以下の通りです。
$$
\mathbf w_{new} = \mathbf w_{old} - \eta \sum\limits_{n=1}^{m}\mathbf \delta_{next, n} \mathbf w_{next, n}f'(\mathbf x_{now})\mathbf a_{pre}
$$$$
\mathbf \delta = \sum\limits_{n=1}^{m}\mathbf \delta_{next, n} \mathbf w_{next, n}f'(\mathbf x_{now})
$$
バックプロぱげーしょんの中間層及び入力層部分は以下の通り。
// middle layer and input layer
// 層の数だけ繰り返す(出力層除く)
for (int i = this.net.layers_num-2; i >= 0; i--){
// 次の層
Node[] nextNodes = this.net.layers[i+1].nodes;
// 着目している層
Node[] nowNodes = this.net.layers[i].nodes;
// 前の層(入力層の場合は存在しないのでここではインスタンス化しない)
Node[] preNodes;
// 次の層のデルタ保管用
Matrix deltas = new Matrix(new double[1][nextNodes.length]);
// 前の層の出力保管用
Matrix preA;
if (i != 0){
// middle layer
// 中間層なら、前の層をインスタンス化し出力を得る
preNodes = this.net.layers[i-1].nodes;
preA = this.calA(preNodes);
}else{
// input layer
// 入力層なら、ネットワークへの入力に重みを加えたものが入力
preA = Matrix.appendCol(x, 1.0);
}
// 次の層のデルタをまとめる
for (int j = 0; j < nextNodes.length; j++){
deltas.matrix[0][j] = nextNodes[j].delta;
}
// ノードごとに繰り返す
for (int j = 0; j < nowNodes.length; j++){
// 着目しているノード
Node nowNode = nowNodes[j];
// 計算用
Matrix cal;
// Σδwf'(x)を一気に計算
nowNode.delta = Matrix.dot(deltas, this.calW(nextNodes, j)).matrix[0][0]
* nowNode.aFunc.differential(nowNode.x.meanCol()).matrix[0][0];
// -ηΣδwf'(x)a
cal = Matrix.mult(preA.meanCol(), -this.eta*nowNode.delta);
// w-Σδwf'(x)
nowNode.w.add(cal.T());
}
}
こちらも怒涛のコメントで申し訳ないです。
まず中間層の場合について説明します。
はじめに、前の層の出力をまとめています。前の層のノード数を仮に10とおくと、これはN行11列となります(バイアスも含めるため)。
次に、次の層のデルタをまとめます。次の層のノード数を仮に5としたとき、deltasは1行5列になります。
ここまでは一つの層の中で共通しますが、ここから先は別なのでノードごとに計算します。
calWメソッドを用いて、着目しているノードからの出力に対して、次の層の各ノードでつけられる重みを取得します。例えば今の層がノードを3個持っているとすると、次の層のノード5個はそれぞれ4行1列の重み行列を所持しています。そして、今の層一つ目のノードからの出力にかけられる重みは5個ある4行1列の行列の、それぞれ1行1列目の数字です。それを集めて5行1列にまとめます。
deltasとcalWでまとめた行列の内積をすることで、スカラが得られます。
これに活性化関数の微分をかけたものが中間層での$\delta$になります。xを平均しているのは、最終層でのaと同じ理由です。
そしてこれに前の層の出力N行11列(こちらも平均して1行11列にする)、そして学習率をかけることで重みが更新できます。前の層のノード数が10ですから、今の層の重み行列は当然11行1列です。転置させて引きました。
入力層については、前の層の出力がネットワークの入力になるだけで同じ流れです。
使ってみた
足し算やってみました。
使用した誤差関数は平均絶対誤差。
import optimizer.*;
import network.*;
import layer.*;
import nodes.activationFunction.*;
import costFunction.*;
import matrix.*;
public class test {
public static void main(String[] str){
// ネットワークの準備
Network net = new Network(
2,
new Input(4, AF.RELU),
new Output(1, AF.LINER)
);
GradientDescent GD = new GradientDescent(
net,
new MeanAbsoluteError()
);
// データ
Matrix X = new Matrix(new double[10][2]);
Matrix T = new Matrix(new double[10][1]);
for (int i = 0; i < X.row; i++){
X.matrix[i][0] = i * 0.1;
X.matrix[i][1] = i * 0.2;
T.matrix[i][0] = X.matrix[i][0] + X.matrix[i][1];
}
MeanAbsoluteError f = new MeanAbsoluteError();
// 30回学習させ、精度表示
Matrix Y = GD.forward(X);
System.out.println(f.calcurate(Y, T));
for (int i = 0; i < 30; i++){
GD.back(X, Y, T);
Y = GD.forward(X);
System.out.println(f.calcurate(Y, T));
}
// 別データで精度確認
for (int i = 0; i < X.row; i++){
X.matrix[i][0] = i * 0.15;
X.matrix[i][1] = i * 0.12;
T.matrix[i][0] = X.matrix[i][0] + X.matrix[i][1];
}
Y = GD.forward(X);
System.out.println("score: ");
System.out.println(f.calcurate(Y, T));
}
}
各学習結果はこちら。
[[1.3821 ]]
[[1.0006 ]]
[[0.5186 ]]
[[0.0878 ]]
[[0.5171 ]]
[[0.0865 ]]
[[0.5160 ]]
[[0.0856 ]]
[[0.5153 ]]
[[0.0851 ]]
[[0.5150 ]]
[[0.0850 ]]
[[0.5151 ]]
[[0.0853 ]]
[[0.5156 ]]
[[0.0860 ]]
[[0.5165 ]]
[[0.0871 ]]
[[0.5178 ]]
[[0.0886 ]]
[[0.5195 ]]
[[0.0906 ]]
[[0.5217 ]]
[[0.0929 ]]
[[0.5242 ]]
[[0.0957 ]]
[[0.5272 ]]
[[0.0989 ]]
[[0.5306 ]]
[[0.1025 ]]
[[0.5345 ]]
行ったり来たりしてます。確認データによる最終誤差はこちら。
score:
[[0.5183 ]]
微妙。
次に、ネットワークを以下のように変更して試してみました。
Network net = new Network(
2,
new Input(4, AF.RELU),
new Dense(10, AF.RELU),
new Output(1, AF.LINER)
);
結果はこちら。
[[2.7587 ]]
[[2.2969 ]]
[[1.9678 ]]
[[1.6999 ]]
[[1.4321 ]]
[[1.2185 ]]
[[1.0253 ]]
[[0.8622 ]]
[[0.7627 ]]
[[0.7040 ]]
[[0.6755 ]]
[[0.6468 ]]
[[0.6239 ]]
[[0.6157 ]]
[[0.6074 ]]
[[0.5990 ]]
[[0.5904 ]]
[[0.5817 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
[[0.5732 ]]
score:
[[0.4964 ]]
なかなか順調に学習できてるんじゃないでしょうか。
確認データによる誤差がなぜか低いことが気になりますが。
ついでに、訓練データと確認データそれぞれについて、このネットワークの予測と正解値を比較してみました。
まず訓練データ。左が予測値、右が正解です。なお表示している行列はMatrixクラスのhstackメソッドで作成しました。
[[0.7414 0.0000 ]
[0.8582 0.3000 ]
[1.0148 0.6000 ]
[1.1304 0.9000 ]
[1.2017 1.2000 ]
[1.2111 1.5000 ]
[1.2445 1.8000 ]
[1.3321 2.1000 ]
[1.4198 2.4000 ]
[1.5075 2.7000 ]]
次に確認データ。左が予測値、右が正解です。
[[0.7414 0.0000 ]
[0.8053 0.2700 ]
[0.9220 0.5400 ]
[1.0308 0.8100 ]
[1.1131 1.0800 ]
[1.1955 1.3500 ]
[1.2100 1.6200 ]
[1.2614 1.8900 ]
[1.3309 2.1600 ]
[1.4005 2.4300 ]]
平均絶対誤差が0.5もあるので、やはりあまり正確ではありませんが、入力データが大きくなるほど出力値も大きくなる正の相関を保ってはいました。
次回は
かなり大変でした。次回何をするかはまだ決めていません。
(追記) 勾配降下法以外の最適化関数を実装しました。
参考文献
番号ふってますが、文の引用などはしていません。深層学習の理解のために参考にさせていただきました。
- Excel関数で学ぶニューラルネットワーク(逆伝播編)|Excelでわかる深層学習の仕組み | LiCLOG
- 初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜 - Qiita
- 【決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法- - Qiita
- 機械学習の要「誤差逆伝播学習法」を解説・実装してみる! – 株式会社ライトコード
- 石川聡彦, 人工知能プログラミングのための数学がわかる本, 株式会社KADOKAWA, 2018年
- 瀧雅人, これならわかる深層学習入門, 株式会社講談社, 2017年
- 岡谷貴之, 深層学習, 株式会社講談社, 2015年