この記事は古川研究室 Advent Calendar 12日目の記事です. 本記事は古川研究室の学生が学習の一環として書いたものです.内容が曖昧であったり表現が多少異なったりする場合があります.
はじめに
研究でmatplotlibを使っていて,単純に便利だったり,ネットで探しても見つかりづらいと感じたtipsをこの記事でまとめて紹介したいと思います.主に自分の備忘録的な話で雑多な内容となっていますが,他の方の参考に少しでもなれば幸いです.
この記事はmatplotlib初級者〜中級者辺りの人を想定しており,一部説明を省いている部分があります.また記事内で紹介しているtipsにはあまり順序はないので,飛ばし飛ばし読んでいただいても問題ないです.
この記事内で紹介するソースコードは全てこちらにあります
https://github.com/tsuno0829/qiita/blob/main/matplotlib_collection/matplotlib_collection.ipynb
1. matplotilbの日本語化
pipもしくはconda経由でjapanize_matplotlibをinstallした状態で,import japanize_matplotlibと宣言するだけでmatplotlib内で日本語が簡単に使えるようになります.シンプルながら非常に便利です.
import matplotlib.pyplot as plt
# matplotlibで日本語を使えるようにするライブラリ.たった1行importするだけでとても簡単
import japanize_matplotlib
plt.text(0.5, 0.5, 'matplotlibで日本語が\n簡単に使えるようになります',fontsize=20,horizontalalignment='center', verticalalignment='center')
plt.show()
2. gifの自動圧縮保存
アニメーションをgif化するときに問題になるのが容量が大きくなりがちになることです.これまではgifを生成したあとに,web上でgifの圧縮を利用したりしていたのですが,アップロードとダウンロードの手間が非常に面倒だったので,このプロセスも自動化してみました.仕組みは非常にシンプルでgif保存後にそのgifに対してImagemagickの圧縮をしているだけです.注意事項としては,gifの容量に比例して圧縮に関しても時間がかかってしまうことです.また,内容次第では想定していたよりも圧縮できないこともあるので期待のしすぎには注意です.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
from matplotlib.colors import ListedColormap
# アニメーション用のデータを作る
n_epoch = 50
n_sample = 150
X = np.zeros((n_epoch, n_sample, 2))
theta = np.linspace(0, 2*np.pi, n_epoch)
for epoch in range(n_epoch):
X[epoch, :, 0] = np.linspace(-3, 3, n_sample)
X[epoch, :, 1] = np.sin(X[epoch, :, 0] + theta[epoch])
# 描画
fig = plt.figure()
ax = fig.add_subplot(111)
# colorのシーケンスを用意する
colors = ListedColormap(sns.color_palette("Spectral", n_epoch))
def update(epoch):
ax.cla()
ax.plot(X[epoch, :, 0], X[epoch, :, 1], color=colors(epoch))
# 学習過程のアニメーションについての宣言
ani = anim.FuncAnimation(fig, update, interval=200, frames=n_epoch, repeat=True)
gif_name = "your_favarite_gif_name.gif"
# 学習した結果をgifで保存
ani.save(gif_name, writer='imagemagick')
# この3行がgifの圧縮に関する部分
# subprocessを使うことで,pythonから直接ターミナルのコマンドを叩くことができるようになるので,
# これを使って既に保存されたgifに対してimagemagickによる圧縮を行う
import subprocess
cmd = "convert " + gif_name + " -layers Optimize " + gif_name
subprocess.call(cmd.split())
3. scatterの高速化
scatterで各点の配色を変えつつ描画をすると,単純な方法ではfor文を回して着色する方法になると思います.しかし,少し工夫することでscatterの描画が高速になることがあります.例えば,2次元のデータに対して,x軸の値が小さいときに紫,大きいときに赤になるような色付けをしたいとします.
データは描画ごとに少しずつ位相がずれていくサインカーブを使います.
# アニメーション用のデータを作る
n_epoch = 50
n_sample = 150
X = np.zeros((n_epoch, n_sample, 2))
theta = np.linspace(0, 2*np.pi, n_epoch)
for epoch in range(n_epoch):
X[epoch, :, 0] = np.linspace(-3, 3, n_sample)
X[epoch, :, 1] = np.sin(X[epoch, :, 0] + theta[epoch])
そのとき,愚直にさっき述べたことをやろうとするとこんな感じになると思います.
def update(epoch):
ax.cla()
t = time.time()
# サインカーブに色付けをして描画する部分
# for文を使って描画をするのがシンプルだが,描画速度は遅い
for i in range(n_sample):
ax.scatter(X[epoch, i, 0], X[epoch, i, 1], color=cm.rainbow(i / n_sample))
fig.suptitle(f'{epoch+1}/{n_epoch}, 1回描画するのにかかった時間:{time.time() - t:.5f}s')
この条件だと大体一回描画するときに0.25秒ぐらいかかることが分かります.
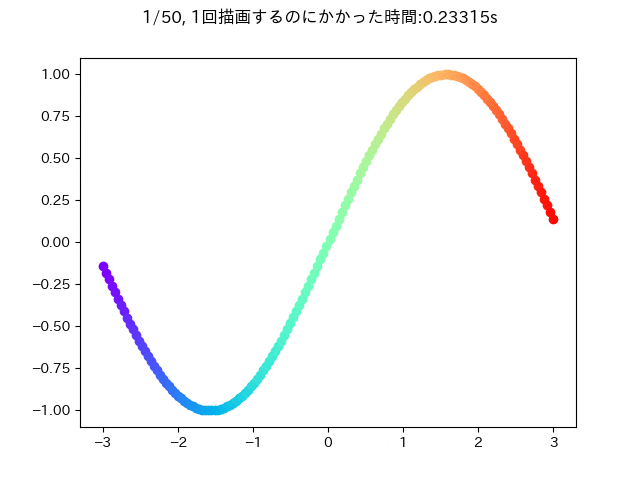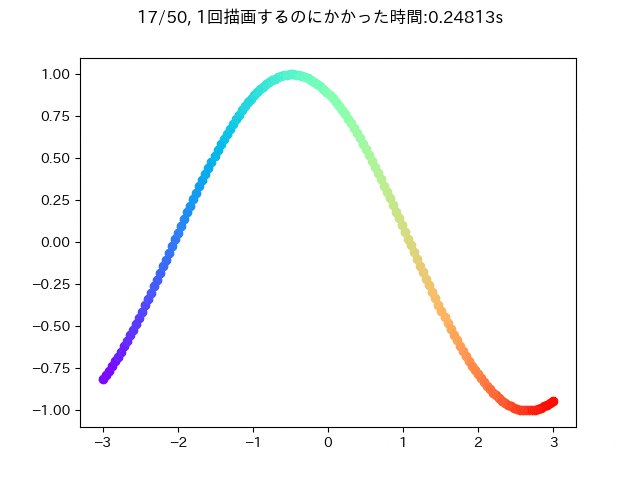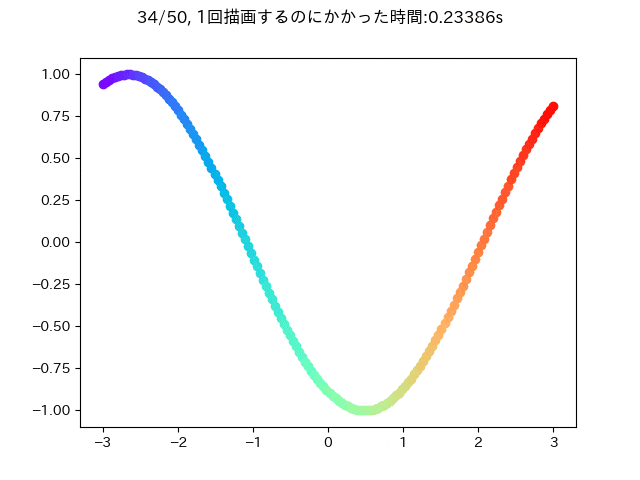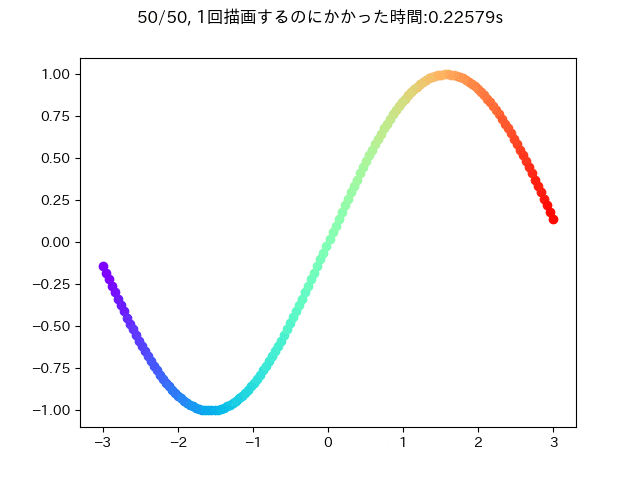
この描画をfor文を使わずにプロットできると嬉しいです.なので次のような感じに変更してみます.
def update(epoch):
ax.cla()
t = time.time()
# 各点に割り当てる色だけを先に用意しておけば,scatterを一度実行するだけでよいのでfor文より描画速度が速い
colors = [cm.rainbow(i/n_sample) for i in range(n_sample)] # 色のリスト
ax.scatter(X[epoch, :, 0], X[epoch, :, 1], color=colors)
fig.suptitle(f'{epoch+1}/{n_epoch}, 1回描画するのにかかった時間:{time.time() - t:.5f}s')
scatterしたい点と各点に割り当てる色のリストを準備して,一回のscatterで点を全て描画するように変更してみました.
このときの実行時間は0.01秒ぐらいです.先程に比べると10倍以上速くなっています.たったこれだけの工夫ですが,複数回for文を使ってプロットするよりも高速になっていることが分かります.
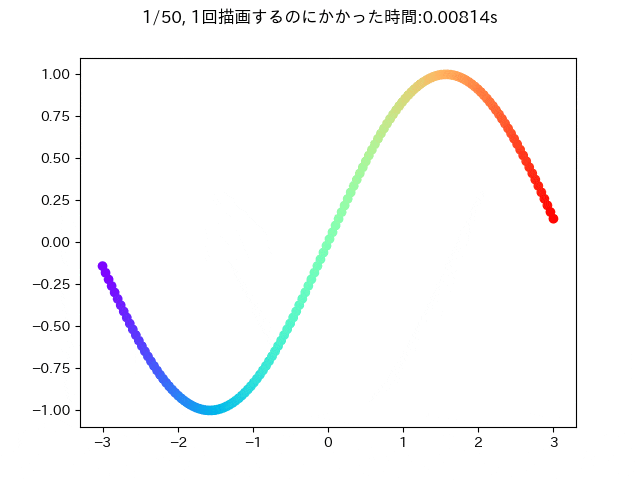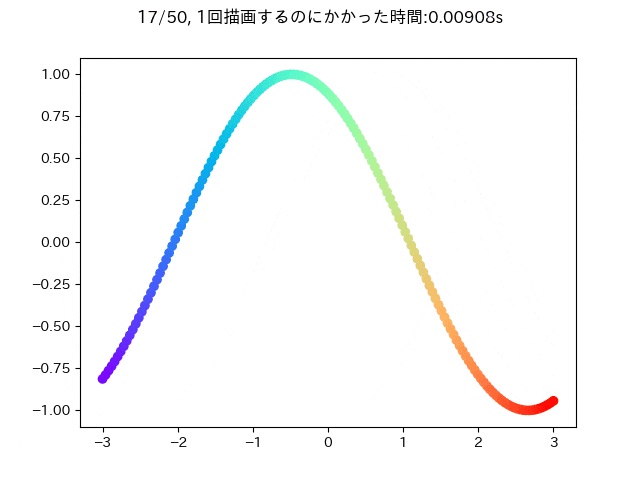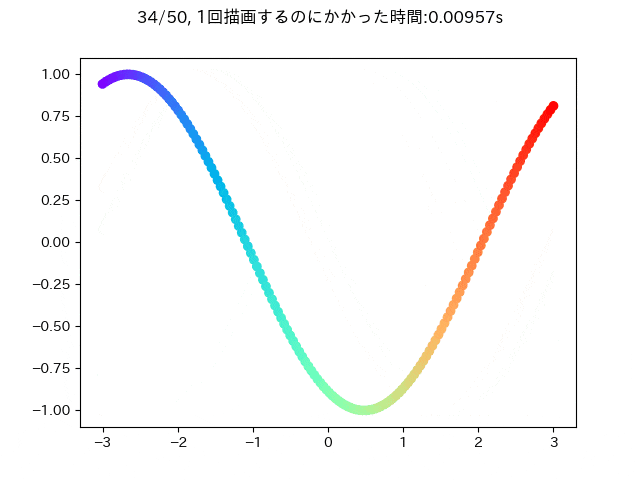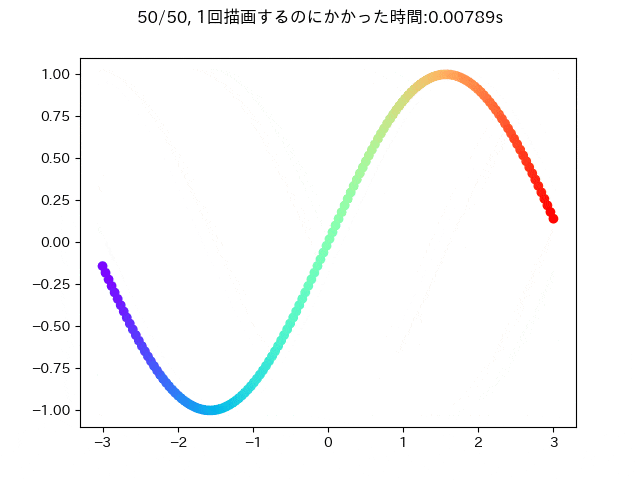
プログラムの全文はこんな感じです
# scatterの各点ごとに色が異なるときの描画をfor文を使わずに高速化
%matplotlib nbagg
import time
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import japanize_matplotlib
# アニメーション用のデータを作る
n_epoch = 50
n_sample = 150
X = np.zeros((n_epoch, n_sample, 2))
theta = np.linspace(0, 2*np.pi, n_epoch)
for epoch in range(n_epoch):
X[epoch, :, 0] = np.linspace(-3, 3, n_sample)
X[epoch, :, 1] = np.sin(X[epoch, :, 0] + theta[epoch])
fig = plt.figure()
ax = fig.add_subplot(111)
def update(epoch):
ax.cla()
t = time.time()
# サインカーブに色付けをして描画する部分(for文)
# for文を使って描画をするのがシンプルだが,描画速度は遅い
# for i in range(n_sample):
# ax.scatter(X[epoch, i, 0], X[epoch, i, 1], color=cm.rainbow(i / n_sample))
# 各点に割り当てる色だけを先に用意しておけば,scatterを一度実行するだけでよいのでfor文より描画速度が速い
colors = [cm.rainbow(i/n_sample) for i in range(n_sample)] # 色のリスト
ax.scatter(X[epoch, :, 0], X[epoch, :, 1], color=colors)
fig.suptitle(f'{epoch+1}/{n_epoch}, 1回描画するのにかかった時間:{time.time() - t:.5f}s')
# 学習過程のアニメーションの表示
ani = anim.FuncAnimation(fig, update, interval=200, frames=n_epoch, repeat=True)
plt.show()
4. plotの高速化
3ではscatterの高速化でしたが,ここではplot(線)も高速化できるtipsを紹介したいと思います(ここは静止画で例を出しますが,アニメーションになったときも同じです).
例に出すデータは2次元のサインデータを使います.各サインデータの違いは,ほんの少しずつ縦にずれています.
n_sin = 100
n_sample = 150
X = np.zeros((n_sin, n_sample, 2))
y_shift = np.linspace(-1, 1, n_sin)
for i in range(n_sin):
X[i, :, 0] = np.linspace(-3, 3, n_sample)
X[i, :, 1] = np.sin(X[i, :, 0]) + y_shift[i]
このサインデータそれぞれに固有の色を与えてプロットしたいとします.まず,シンプルにfor文を使って実装するとこんな感じになります.
colors = [cm.rainbow(i/n_sin) for i in range(n_sin)] # 色のリスト
t = time.time()
# for文で描画
for i in range(n_sin):
ax.plot(X[i, :, 0], X[i, :, 1], color=colors[i])
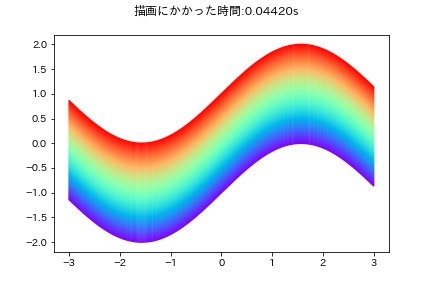
fig.suptitle(f'描画にかかった時間::{time.time() - t:.5f}s')
一番上のサインカーブが赤色,一番下のサインカーブを紫色として描画しています.ここでは,大体0.04秒ぐらいで描画できています.
では,続いてfor文を使わずに描画する例を紹介したいと思います.
ここでは,LineCollectionの機能を使います.web検索では,あまり日本語の情報が見つかりませんがmatplotlib公式の例がわかりやすいです.ポイントは,描画したいplot(Line2d)の集合を全てLineCollectionのリストに保存してしまい,一度に全て描画してしまうということです.
https://matplotlib.org/3.3.3/gallery/shapes_and_collections/line_collection.html
https://teratail.com/questions/269922
# 描画
colors = [cm.rainbow(i/n_sin) for i in range(n_sin)] # 色のリスト
t = time.time()
# LineCollectionによる描画
lines = np.array([X[i] for i in range(n_sin)])
lc = mc.LineCollection(lines, colors=colors)
ax.add_collection(lc)
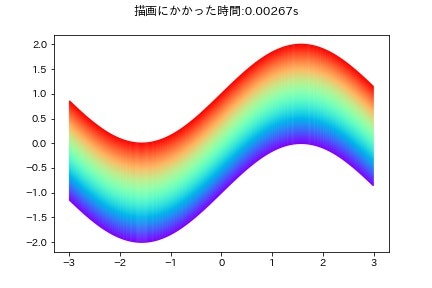
fig.suptitle(f'描画にかかった時間::{time.time() - t:.5f}s')
# autoscaleをつけないと描画が拡大したような感じになるのでLineCollectionを使うときは必須です
ax.autoscale()
この方法で描画すると大体0.003秒になっており,for文を使って描画するよりも10倍高速化できていることが分かります.静止画であればfor文による実装でも問題ないですが,アニメーションを使うときはfor文がボトルネックとなる可能性があるのでこちらの方法を採用したほうがいいかもしれません.
プログラムの全文はこちらです.
# plotも高速化(アニメーションの例が思いつかなかったので,ここは静止画です)
%matplotlib inline
import time
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import matplotlib.collections as mc
n_sin = 100
n_sample = 150
X = np.zeros((n_sin, n_sample, 2))
y_shift = np.linspace(-1, 1, n_sin)
for i in range(n_sin):
X[i, :, 0] = np.linspace(-3, 3, n_sample)
X[i, :, 1] = np.sin(X[i, :, 0]) + y_shift[i]
fig = plt.figure()
ax = fig.add_subplot(111)
# 描画
colors = [cm.rainbow(i/n_sin) for i in range(n_sin)] # 色のリスト
t = time.time()
# for文で描画
# for i in range(n_sin):
# ax.plot(X[i, :, 0], X[i, :, 1], color=colors[i])
# LineCollectionによる描画
lines = np.array([X[i] for i in range(n_sin)])
lc = mc.LineCollection(lines, colors=colors)
ax.add_collection(lc)
fig.suptitle(f'描画にかかった時間:{time.time() - t:.5f}s')
# autoscaleをつけないと描画が拡大したような感じになるのでLineCollectionを使うときは必須です
ax.autoscale()
plt.show()
5. 2次元のplot_wireframeを作る
(こちらは4でやったことの応用になっており,中身は全く同じになります)
3次元のwireframeをmatplotlibで描画すると例えば下記のようになります.
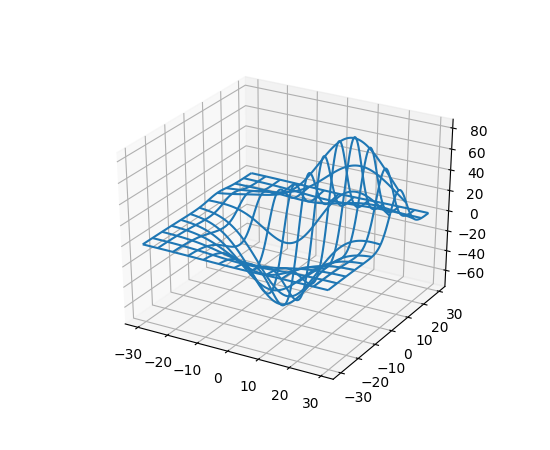
https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html から引用
ここで,このようなメッシュによる描画は3次元空間にのみ用意されており,2次元空間に対してのwireframeは用意されていません.個人的に,2次元の場合でも描画したくなることがあったのですがwebで検索しても日本語の記事が全然でてこなかったのでここで説明します.ただ難しいことは何もなく,wireframeは単にplotの集合で表現できることから6でやったことと同じことをするだけです.具体的な方法は下記のstackoverflowを参考にしています.
https://stackoverflow.com/questions/47295473/how-to-plot-using-matplotlib-python-colahs-deformed-grid
今回は簡単のため格子状のwireframeを描画してみます.
# wireframeで表示したデータの作成
# resolutionはmeshの細かさを表しています
resolution = 20
x = y = np.linspace(-1, 1, resolution)
grid_x, grid_y = np.meshgrid(x, y)
segs1 = np.stack((grid_x, grid_y), axis=2)
segs2 = segs1.transpose(1, 0, 2) # segs1に対して交差するようにplotしたいので転置する
segs = np.r_[segs1,segs2]
描画部分はこんな感じです
# 描画
colors = [cm.rainbow(i/len(segs)) for i in range(len(segs))] # 色のリスト
fig = plt.figure()
ax = fig.add_subplot(111, aspect=True)
ax.add_collection(mc.LineCollection(segs, linewidth=2, colors=colors))
ax.autoscale()
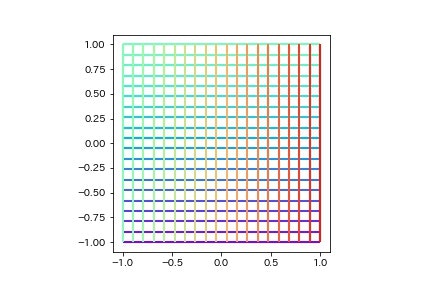
plt.show()
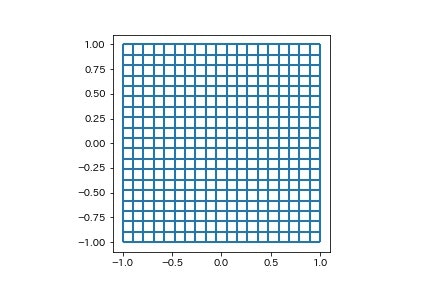
着色は普通必要ないと思いますが,線(Line2D)の集合であることを示すためにわざとつけています.LineCollectionのcolorsを特に指定しないとこんな感じで最初に示したwireframeのようになります.
プログラムの全文はこんな感じです.
# 2次元版のplot_wireframeを作る
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.collections as mc
# wireframeで表示したデータの作成
# resolutionはmeshの細かさを表しています
resolution = 20
x = y = np.linspace(-1, 1, resolution)
grid_x, grid_y = np.meshgrid(x, y)
segs1 = np.stack((grid_x, grid_y), axis=2)
segs2 = segs1.transpose(1, 0, 2)
segs = np.r_[segs1,segs2]
# 描画
colors = [cm.rainbow(i/len(segs)) for i in range(len(segs))] # 色のリスト
fig = plt.figure()
ax = fig.add_subplot(111, aspect=True)
ax.add_collection(mc.LineCollection(segs, linewidth=2, colors=colors))
ax.autoscale()
plt.show()
6.差分更新による高速化
matplotlibで描画を高速化したいときに,更新したい部分だけ変更し(例えばscatterやplotの座標など),それ以外の再利用できるものはそのままにしておくことで描画を高速化できることがあります.詳細は,下記の記事が参考になります.
https://waregawa-log.hatenablog.com/entry/2019/02/09/192939
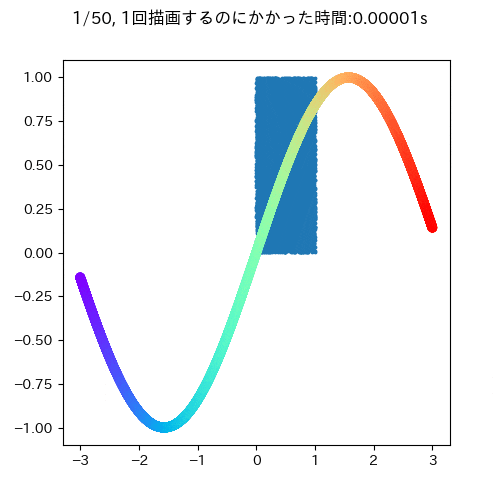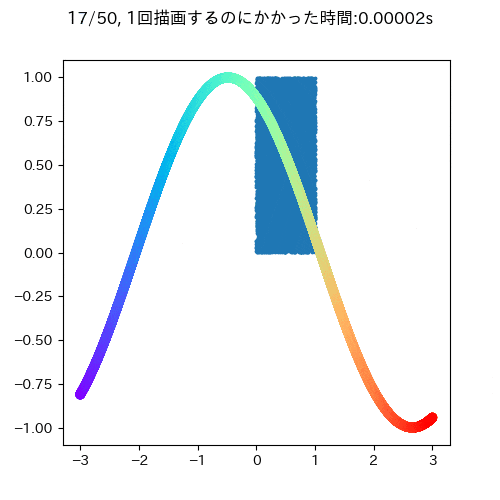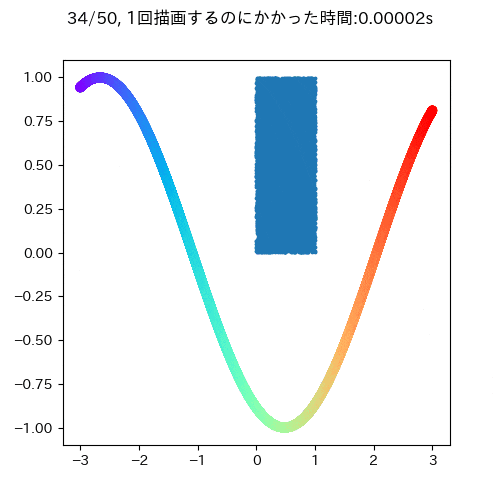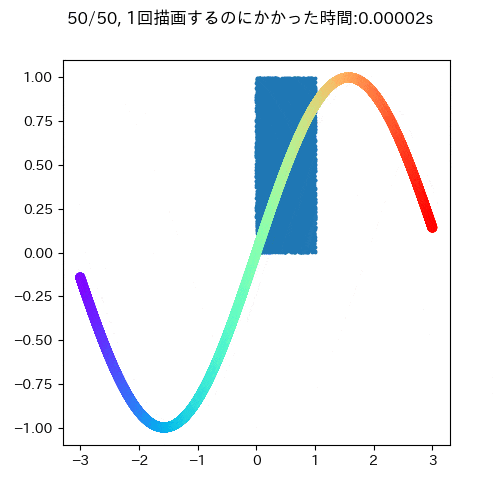
ここでは,時間的に変化がないものと変化があるものを同時にアニメーションで描画するケースを差分更新なしとありの状況で試してみます(機械学習でいうと学習データ(固定)と推定結果(学習回数により可変)みたいなものを描画するイメージでしています).
n_epoch = 50
n_sample = 50000
# 時間によって結果が変わるデータを作成
X1 = np.zeros((n_epoch, n_sample, 2))
theta = np.linspace(0, 2*np.pi, n_epoch)
for epoch in range(n_epoch):
X1[epoch, :, 0] = np.linspace(-3, 3, n_sample)
X1[epoch, :, 1] = np.sin(X1[epoch, :, 0] + theta[epoch])
# 時間によって変わらないデータを作成
X2 = np.random.rand(n_sample, 2)
まずは普通に描画をしてみます.
# 描画
fig = plt.figure(figsize=(4, 4))
ax = fig.add_subplot(1,1,1)
colors = [cm.rainbow(i/n_sample) for i in range(n_sample)] # 色のリスト
def update(epoch):
ax.cla()
t = time.time()
ax.scatter(X1[epoch, :, 0], X1[epoch, :, 1], color=colors)
ax.scatter(X2[:,0], X2[:,1], s=3, zorder=0)
fig.suptitle(f'{epoch+1}/{n_epoch}, 1回描画するのにかかった時間:{time.time() - t:.5f}s')
# 学習過程のアニメーションの表示
ani = anim.FuncAnimation(fig, update, interval=1, frames=n_epoch, repeat=True)
plt.show()
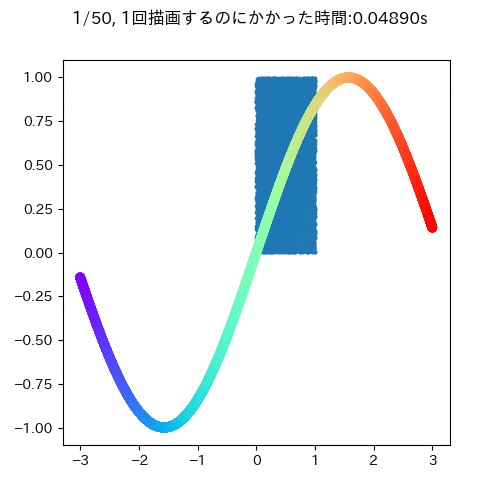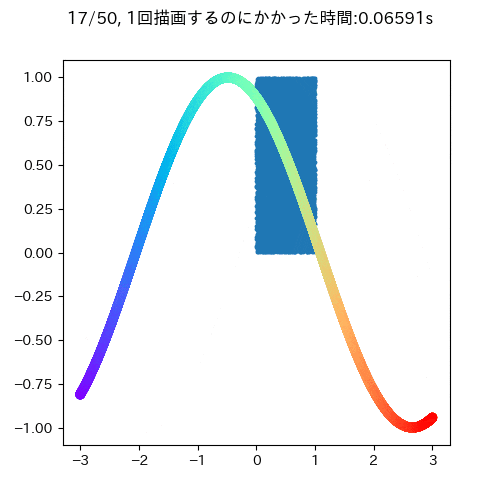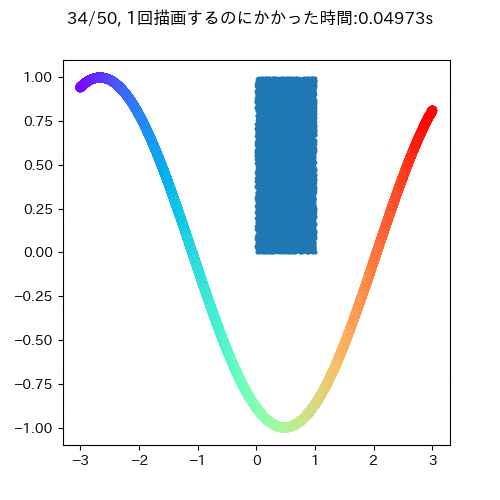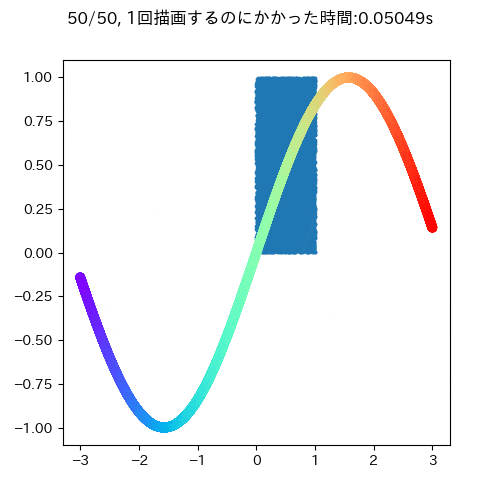
青い四角が時間的に変化しないもので,サインカーブが時間的に変化するデータです.
大体一回の描写に0.05秒ぐらいかかります.また,このgifを見ても明らかなようにサインカーブとタイトルだけ描画すればよく,変わっていないもの消して再描画する必要はないことがわかります(データが少ないうちはいいですが,多いデータだとこの部分が描画のボトルネックになる可能性があります)
差分更新では,この変化する部分だけを変更することで描画を高速化します.具体的はコードは下記です.
# 差分更新したいときはこうして,objectを参照できるように変数を作っておく
scat_X1 = ax.scatter(X1[0, :, 0], X1[0, :, 1], color=colors)
# 時間的に変化しないものに関しては,update関数の外に一度描画しておくだけ
ax.scatter(X2[:,0], X2[:,1], s=3, zorder=0)
def update(epoch):
t = time.time()
# 更新したいデータ点のみ変更する.今回のケースでは,objectの座標のみを変更したいのでset_offsetsに新しい座標を入力する
scat_X1.set_offsets(X1[epoch])
fig.suptitle(f'{epoch+1}/{n_epoch}, 1回描画するのにかかった時間:{time.time() - t:.5f}s')
# 学習過程のアニメーションの表示
ani = anim.FuncAnimation(fig, update, interval=200, frames=n_epoch, repeat=True)
plt.show()
scat_X1という変数は,<matplotlib.collections.PathCollection object at 0x115d486d0>でオブジェクトです.このオブジェクトの座標だけをupdate関数内で変更することで効率的な描画ができます.このアニメーションで得られたgifが以下のようになります.
結果を見ても明らかなように,差分更新をすることで訳1000倍描画を高速化できていることが分かりました(既にgif化しているのでgifの速度は同じですが,plt.show()でアニメーションを見てみると速度が異なることが分かります).また,今回のケースではscatterだけを取り上げましたが,plot等の他の描画でも同じようなことができます.ただ,自分が確認したところヒストグラムやwireframeについては見つけることができませんでした.また,3次元のケースでも散布図の場合ax._offsets3d = (X[:, 0], X[:, 1], X[:, 2])みたい感じで一応差分更新ができるようなのですが,自分が試した限りではあまり期待していたような結果が得られなかったのでここでは触れていません.
7.GridSpecを使ったsubplot
複数のsubplotを作るときに,Gridspecを使うと簡単に思い通りのものが作れるようになるのでここで紹介します.
描画に使うデータはこんな感じです.色々設定していますが特に深い意味はなく,何でも構いません.
# プロットで描画するデータを準備
# 3d用
n_sample = 1000
X = np.zeros(shape=(n_sample, 3))
data = np.random.rand(n_sample, 2) * 2 - 1
mesh = data[:, 0] ** 2 - data[:, 1] ** 2
X[:, 0] = data[:, 0]
X[:, 1] = data[:, 1]
X[:, 2] = mesh
# Xの各点に色を割り当てる.sklearnのMinMaxScalerを使って各軸について0~1になるように正規化し,その値をXのRGB値にする
mmscaler = preprocessing.MinMaxScaler()
mmscaler.fit(X)
X_RGB = mmscaler.transform(X)
# 2d用
Z = np.random.normal(loc=0, scale=0.1, size=(n_sample, 2))
# loss用
loss = np.exp(-0.1*np.linspace(1, 100, 100))
続いて描画です.figを作った後にGridspecを使ってaxesに関する細かい設定をしたあとにfig.add_subplotで各axesを生成しています.Gridspecの詳細な使い方については,とてもわかり易い解説記事が既にあるのでそちらを参考にしてみてください.
https://qiita.com/simonritchie/items/da54ff0879ad8155f441
描画部分のコードは今回はこんな感じにしてみました.
# 描画
fig = plt.figure(figsize=(12, 8))
gs_master = GridSpec(nrows=4, ncols=2, hspace=1)
gs_3d = GridSpecFromSubplotSpec(nrows=3, ncols=1, subplot_spec=gs_master[:-1, 0:1])
gs_2d = GridSpecFromSubplotSpec(nrows=2, ncols=1, subplot_spec=gs_master[:-2, 1:2])
gs_param = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[-1:, 0:1])
gs_loss = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[-2:, 1:2])
ax_3d = fig.add_subplot(gs_3d[:, :], projection='3d')
ax_2d = fig.add_subplot(gs_2d[:, :], aspect=True)
ax_param = fig.add_subplot(gs_param[:, :])
ax_loss = fig.add_subplot(gs_loss[:, :])
ax_3d.scatter(X[:, 0], X[:, 1], X[:, 2], color=X_RGB)
ax_2d.scatter(Z[:, 0], Z[:, 1], color=X_RGB)
ax_loss.plot(np.arange(len(loss)), loss)
ax_param.text(0.5, 0.5, 'test', fontsize=15,
horizontalalignment='center', verticalalignment='center', transform=ax_param.transAxes)
ax_param.xaxis.set_visible(False), ax_param.yaxis.set_visible(False)
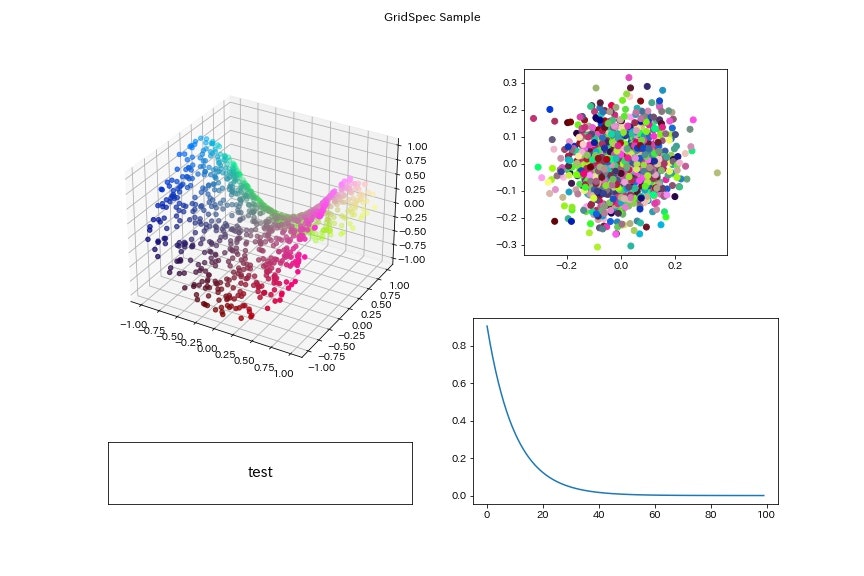
plt.suptitle('GridSpec Sample')
plt.show()
結果はこんな感じで,1つのfigureに4つも描画しましたが自分でサイズ感を自由に設定しつつも簡単に描画できました.ここで紹介していない余白の調整等の細かい設定もGridSpecを使うと簡単に設定できます.これらを通常のsubplotで作ろうとすると大変ですが,GridSpecだと一瞬なので使ったことがない人は是非使ってみることをおすすめします.
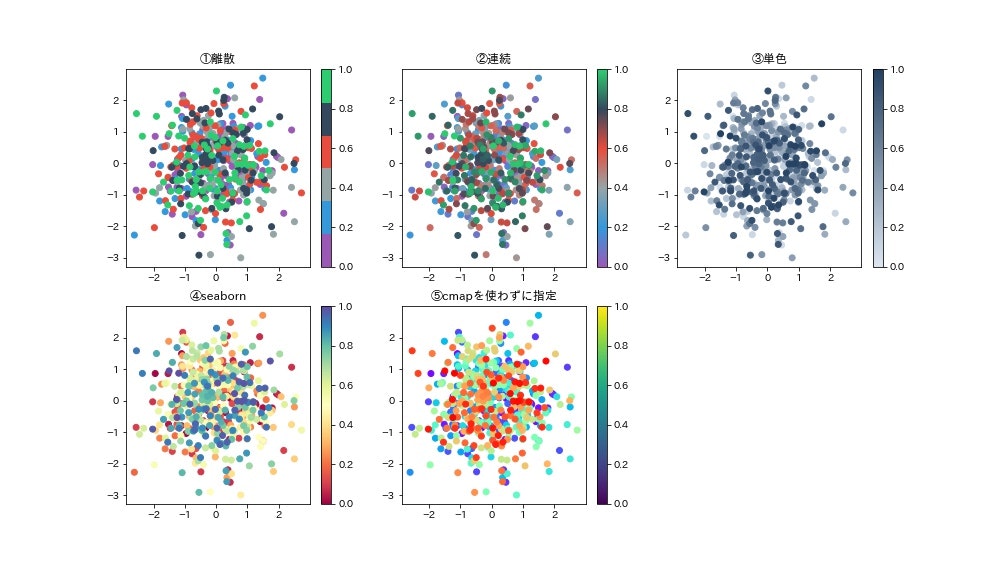
8. color mapの作り方など
color mapで引っかかることが多いので関連するものを色々並べます.ここでは先にここで紹介する全部の結果を載せておきます.
また,colormapについて理解するには下記の記事がわかりやすいです.
https://qiita.com/HidKamiya/items/524d77e3b53a13849f1a
①②③離散的,連続的なcolormapの作り方
matplotlib.colorsのListedColormapとLinearSegmentedColormapを使って作ります.
色はこちらが指定した配色にできます.
# color_mapの作り方
color_list = ["#9b59b6", "#3498db", "#95a5a6", "#e74c3c", "#34495e", "#2ecc71"]
# 離散的に色が変わるcmapの作り方
cmap1 = ListedColormap(sns.color_palette(color_list, 6))
# 連続的に色が変わるcmapの作り方
cmap2 = LinearSegmentedColormap.from_list(name='continuous', colors=color_list, N=256)
# 単色のcmapの作り方(Nは解像度)
cmap3 = LinearSegmentedColormap.from_list(name='custom blue', colors=['#DCE6F1', '#244162'], N=256)
scat_ax1 = ax1.scatter(data1, data2, c=colors, cmap=cmap1)
fig.colorbar(scat_ax1, ax=ax1)
scat_ax2 = ax2.scatter(data1, data2, c=colors, cmap=cmap2)
fig.colorbar(scat_ax2, ax=ax2)
scat_ax3 = ax3.scatter(data1, data2, c=colors, cmap=cmap3)
fig.colorbar(scat_ax3, ax=ax3)
④seabornのcmapの使い方
matplotlib以外のcmapを使うことができます.ここでは,seabornのcmapを使います.やり方も単純で以下のようにListedColormapの中にseabornのcolor_paletteを入れるだけです.
# seabornのcmapを使う方法
cmap4 = ListedColormap(sns.color_palette("Spectral", 256))
scat_ax4 = ax4.scatter(data1, data2, c=colors, cmap=cmap4)
fig.colorbar(scat_ax4, ax=ax4)
⑤cmapを使わずに色を指定する方法
余談ではありますが,cmapを使わずに描画に色を指定することもできます.やり方は下記のような感じで全てのデータに対して直接color引数にRGB値(を要素に持つデータと同じ長さのリスト)を与えるだけです.ただし,colorbarを表示するときにはデフォルトのものが出てしまうようなので注意が必要です.
# cmapを指定せすにcolorでデータの着色もできるがcolor barはデフォルトの設定のままなようです(colorbarとの不一致をどう解消すればいいのかは不明です)
colors = [cm.rainbow(i/N) for i in range(N)] # 色のリスト
scat_ax5 = ax5.scatter(data1, data2, color=colors)
fig.colorbar(scat_ax5, ax=ax5)
9. 3次元を描画するときのset_aspect('equal')のやり方
matplotlibの3次元を描画をするときに,ax.set_aspect('equal')をしても2次元のときのように上手くいきません.ここでは,下記記事を参考に3次元の描画のset_aspect('equal')ど同様の処理を実装してみます(コードは記事内のものをお借りてしています)
https://qiita.com/ae14watanabe/items/71f678755525d8088849
使用するデータはここでは下記コードのように生成しました.特徴として,XとYに対して異常にZのスケールを大きくしてみました.
# 使用するデータ
# Z軸だけわざとスケールを50倍にしています.
n_sample = 1000
data = np.random.rand(n_sample, 2) * 2 - 1
X = data[:, 0]
Y = data[:, 1]
Z = (data[:, 0] ** 2 - data[:, 1] ** 2) * 50
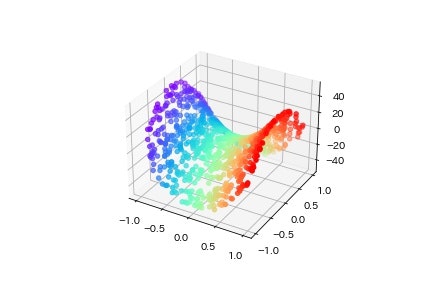
描画関数はこんな感じです.このデータを描画すると本当はZ方向に非常に長く,XとYはZに対してはノイズのように描画されてほしいのですが普通に描画してしまうと以下のようになってしまいます.
fig = plt.figure()
ax = fig.add_subplot(111,projection='3d')
ax.scatter(X, Y, Z, c=X, cmap='rainbow')
plt.show()
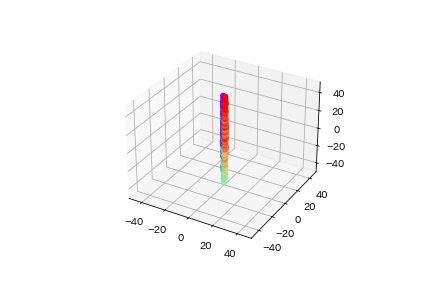
期待通りの結果を得るためにはscatterとplt.show()の間に以下のコードをはさみます.
max_range = np.array([X.max()-X.min(), Y.max()-Y.min(), Z.max()-Z.min()]).max() * 0.5
mid_x = (X.max()+X.min()) * 0.5
mid_y = (Y.max()+Y.min()) * 0.5
mid_z = (Z.max()+Z.min()) * 0.5
ax.set_xlim(mid_x - max_range, mid_x + max_range)
ax.set_ylim(mid_y - max_range, mid_y + max_range)
ax.set_zlim(mid_z - max_range, mid_z + max_range)
(余談:こういう処理をわざわざしないといけないことからも分かるように,matplotlibの3次元の描画は色々と不足しているところがあるなぁと最近感じることが多くなってきました.他の描画ライブラリだとここらへんも上手く実装できているんでしょうか…)
10. legendの位置調整
個人的にlegendの位置調整をする機会がよくあり,下記記事を非常にわかりやすいのでオススメです.
https://qiita.com/matsui-k20xx/items/291400ed56a39ed63462
上記記事の内容が全てなのですが,自分のケースでは図の右上にlegendを置くことが多いので一応ここでやってみます.
# legendの位置調整
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from matplotlib.gridspec import GridSpec, GridSpecFromSubplotSpec
# データの作成
n_epoch = 50
n_sample = 150
X = np.zeros((n_sample, 2))
X[:, 0] = np.linspace(-3, 3, n_sample)
X[:, 1] = np.sin(X[:, 0])
fig = plt.figure(figsize=(7, 6))
gs_master = GridSpec(nrows=2, ncols=2, hspace=0.5, wspace=0.5)
gs1 = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[:1, 0:1])
gs2 = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[:1, 1:2])
gs3 = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[1:, 0:1])
gs4 = GridSpecFromSubplotSpec(nrows=1, ncols=1, subplot_spec=gs_master[1:, 1:2])
ax1 = fig.add_subplot(gs1[:, :])
ax2 = fig.add_subplot(gs2[:, :])
ax3 = fig.add_subplot(gs3[:, :])
ax4 = fig.add_subplot(gs4[:, :])
c_linspace = np.linspace(1, 0, 4, endpoint=True)
ax1.plot(X[:, 0], X[:, 1], color=cm.rainbow(c_linspace[0]), label='sin1')
ax2.plot(X[:, 0], X[:, 1], color=cm.rainbow(c_linspace[1]), label='sin2')
ax3.plot(X[:, 0], X[:, 1], color=cm.rainbow(c_linspace[2]), label='sin3')
ax4.plot(X[:, 0], X[:, 1], color=cm.rainbow(c_linspace[3]), label='sin4')
ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0.5)
ax2.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
ax3.legend(bbox_to_anchor=(1, 1), loc='lower right', borderaxespad=0.5)
ax4.legend(bbox_to_anchor=(1, 1), loc='lower left', borderaxespad=0.5)
plt.show()
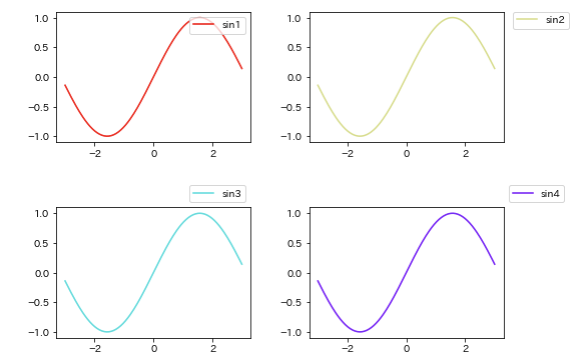
右上にlegendを置くだけでもいろいろ設定できることがわかります.
まとめ
matplotlibで細かいことをしようとすると,途端に難しさが増していくことを身をもって体験しました.この記事が少しでも誰かの参考になれば幸いです.